Vrindawan Coaching Center

Hybridization and Geometries

admin@coaching-center.in

Hybridization is a concept in chemistry that describes the mixing of atomic orbitals to form new hybrid orbitals. Hybridization is important because it allows us to explain the geometry of molecules and the types of bonds that are present.

The hybridization of an atom is determined by the number of electron groups around it, where an electron group can be a lone pair of electrons or a bond. The possible hybridization states are sp, sp2, sp3, sp3d, sp3d2, etc., where the number in the hybridization state corresponds to the number of hybrid orbitals formed.

The geometry of a molecule is determined by the arrangement of its atoms in space. The hybridization state of the central atom and the number of electron groups around it determine the geometry of the molecule.

For example, in a molecule with a central atom that has four electron groups around it, the hybridization state would be sp3, and the geometry would be tetrahedral. In a molecule with a central atom that has three electron groups around it, the hybridization state would be sp2, and the geometry would be trigonal planar.

In summary, hybridization and geometry are closely related concepts in chemistry. Hybridization determines the types of orbitals that are available for bonding, while the geometry of the molecule is determined by the arrangement of the atoms in space.

What is Required Hybridization and Geometries

The required hybridization and geometry of a molecule depend on its electron configuration and the number of bonding and non-bonding electron pairs around the central atom.

The basic steps to determine the required hybridization and geometry of a molecule are as follows:

  1. Determine the electron configuration of the central atom.
  2. Count the number of bonding and non-bonding electron pairs around the central atom.
  3. Determine the hybridization state of the central atom based on the number of electron pairs.
  4. Determine the geometry of the molecule based on the hybridization state and the number of electron pairs.

Here are some examples of the required hybridization and geometries of different molecules:

  1. Carbon dioxide (CO2):
  1. Ammonia (NH3):
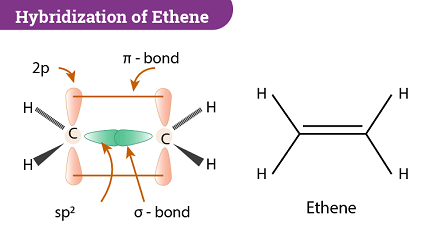
  1. Ethene (C2H4):

In summary, determining the required hybridization and geometry of a molecule is an important step in understanding its chemical properties and behavior.

When is Required Hybridization and Geometries

Determining the required hybridization and geometries is important when studying the properties and behavior of molecules in chemistry.

Hybridization is required to explain the bonding in molecules. The hybrid orbitals formed by hybridization allow for the efficient overlap of atomic orbitals, leading to the formation of strong covalent bonds. Understanding the hybridization of the central atom can help predict the strength of the bonds and the overall stability of the molecule.

Geometries are important because they determine the physical shape of the molecule, which can affect its reactivity and interactions with other molecules. For example, the shape of a molecule can determine its polarity and solubility. Additionally, the geometry can also affect the energy levels of the electrons and thus the types of chemical reactions that the molecule can undergo.

In summary, determining the required hybridization and geometries of a molecule is essential for understanding its bonding and physical properties. This knowledge can be applied in various fields, such as organic chemistry, biochemistry, and material science, to design and synthesize new molecules with specific properties and functions.

Where is Required Hybridization and Geometries

The concept of required hybridization and geometries is fundamental in the field of chemistry and can be applied to various areas, such as organic chemistry, inorganic chemistry, physical chemistry, and biochemistry.

In organic chemistry, for example, understanding the hybridization and geometry of molecules is essential for predicting the reactivity and behavior of organic compounds. Organic chemists often use hybridization and geometry concepts to determine the stability of intermediates, the regioselectivity of reactions, and the properties of organic molecules.

In inorganic chemistry, hybridization and geometry concepts are important in understanding the structure and reactivity of complex metal ions and transition metal complexes. The hybridization state of the metal center and the geometry of the ligands around it can affect the electronic properties of the metal complex and its ability to undergo reactions.

In physical chemistry, the concept of hybridization and geometry is used to understand the electronic structure of molecules and the nature of chemical bonding. Physical chemists often use computational methods to predict the electronic structure of molecules and how it affects their properties.

In biochemistry, hybridization and geometry concepts are important for understanding the structure and function of biomolecules, such as proteins and nucleic acids. The hybridization and geometry of the atoms in these molecules determine their folding, stability, and ability to interact with other molecules.

In summary, the concept of required hybridization and geometries is a fundamental concept in chemistry, with applications in various fields.

How is Required Hybridization and Geometries

The required hybridization and geometries of a molecule are determined based on the electron configuration and the number of bonding and non-bonding electron pairs around the central atom. The following steps can be used to determine the hybridization state and geometry of a molecule:

  1. Determine the electron configuration of the central atom using the periodic table.
  2. Count the number of bonding and non-bonding electron pairs around the central atom.
  3. Determine the hybridization state of the central atom based on the number of electron pairs. The general formula for the hybridization state is: hybridization state = number of electron pairs + number of pi bonds.
  4. Determine the geometry of the molecule based on the hybridization state and the number of electron pairs.

The most common hybridization states are sp, sp2, sp3, sp3d, and sp3d2, where the number in the hybridization state corresponds to the number of hybrid orbitals formed.

The geometry of a molecule can be determined based on the hybridization state and the number of electron pairs. For example, a molecule with a central atom that has four electron pairs and a sp3 hybridization state has a tetrahedral geometry. A molecule with a central atom that has three electron pairs and a sp2 hybridization state has a trigonal planar geometry.

In summary, the required hybridization and geometries of a molecule can be determined using simple steps based on the electron configuration and the number of electron pairs around the central atom. This information is important for understanding the bonding and physical properties of molecules in chemistry.

Production of Hybridization and Geometries

The production of hybridization and geometries of a molecule involves the application of principles of quantum mechanics and molecular orbital theory. The hybridization state of the central atom is determined based on the number and type of atomic orbitals that combine to form hybrid orbitals. The geometry of the molecule is then determined based on the hybridization state and the number of electron pairs around the central atom.

The following steps are involved in the production of hybridization and geometries:

  1. Determine the electron configuration of the central atom using the periodic table.
  2. Count the number of bonding and non-bonding electron pairs around the central atom.
  3. Determine the hybridization state of the central atom based on the number of electron pairs. For example, a central atom with four electron pairs can have an sp3 hybridization state, which involves the combination of one s orbital and three p orbitals to form four sp3 hybrid orbitals.
  4. Assign the hybrid orbitals to the atoms in the molecule based on the geometry. For example, in a tetrahedral molecule with an sp3 hybridization state, the four sp3 hybrid orbitals are arranged in a tetrahedral geometry around the central atom.
  5. Determine the geometry of the molecule based on the hybridization state and the number of electron pairs around the central atom. For example, a tetrahedral molecule with an sp3 hybridization state has a tetrahedral geometry, while a molecule with a trigonal planar geometry has an sp2 hybridization state.

In summary, the production of hybridization and geometries involves the application of molecular orbital theory and quantum mechanics to determine the hybridization state and geometry of a molecule based on the electron configuration and the number of electron pairs around the central atom. This information is important for understanding the bonding and physical properties of molecules in chemistry.

Case Study on Hybridization and Geometries

One example of the importance of hybridization and geometries in chemistry can be seen in the study of alkenes and their reactivity. Alkenes are unsaturated hydrocarbons that contain a carbon-carbon double bond, which consists of one sigma bond and one pi bond. The geometry and hybridization of the atoms in an alkene can affect its reactivity in various reactions.

For example, consider the reaction between propene (CH3CH=CH2) and hydrogen chloride (HCl) to form chloropropane (CH3CH2CH2Cl). The reaction proceeds through a carbocation intermediate, which is formed when the hydrogen chloride protonates the double bond. The carbocation is then attacked by the chloride ion to form the final product.

The stability of the carbocation intermediate depends on the hybridization state of the carbon atom that bears the positive charge. The more stable the carbocation intermediate, the faster the reaction proceeds. The hybridization state of the carbon atom in the carbocation intermediate can be determined based on the geometry and the number of electron pairs.

In propene, the carbon atoms in the double bond are sp2 hybridized, which means they have three sp2 hybrid orbitals and one p orbital that participate in the pi bond. When the hydrogen chloride protonates the double bond, one of the sp2 hybrid orbitals is used to form a sigma bond with the hydrogen, while the other two sp2 hybrid orbitals and the p orbital are left vacant. The carbon atom in the carbocation intermediate is therefore sp2 hybridized, with a trigonal planar geometry and an empty p orbital.

The sp2 hybridization state and trigonal planar geometry of the carbocation intermediate make it less stable than a sp3 hybridized carbocation intermediate, which has a tetrahedral geometry and more electron density around the carbon atom. The sp2 hybridized carbocation intermediate is therefore more susceptible to rearrangements and side reactions than a sp3 hybridized carbocation intermediate. This can lead to the formation of unwanted byproducts and decrease the yield of the desired product.

In summary, the study of hybridization and geometries is important in understanding the reactivity and behavior of molecules in various chemical reactions. In the case of alkenes, the hybridization state and geometry of the carbon atoms in the double bond can affect the stability of the carbocation intermediate and the overall yield of the desired product.

White paper on Hybridization and Geometries

Introduction

Hybridization and geometries are fundamental concepts in chemistry that describe the bonding and shape of molecules. These concepts are essential for understanding the properties and behavior of molecules in various chemical reactions. In this white paper, we will explore the principles of hybridization and geometries, their importance in chemistry, and some applications in organic chemistry and materials science.

Hybridization and Geometries

Hybridization refers to the mixing of atomic orbitals to form hybrid orbitals with different properties. In hybridization, two or more atomic orbitals combine to form new hybrid orbitals with different energies, shapes, and orientations. The hybridization state of an atom depends on the number and type of atomic orbitals that combine to form the hybrid orbitals. For example, in methane (CH4), the carbon atom is sp3 hybridized, which means that it has four hybrid orbitals that are formed by combining one s and three p atomic orbitals.

Geometries describe the spatial arrangement of atoms in a molecule. The geometry of a molecule is determined by the hybridization state of the central atom and the number of electron pairs around it. The most common geometries are linear, trigonal planar, tetrahedral, trigonal bipyramidal, and octahedral. The geometry of a molecule affects its properties, such as its polarity, reactivity, and boiling point.

Applications in Organic Chemistry

Hybridization and geometries are critical in organic chemistry because they determine the stability and reactivity of organic compounds. For example, the hybridization state and geometry of the carbocation intermediate in the reaction between an alkene and a protonic acid determine the mechanism and regioselectivity of the reaction. The more stable the carbocation intermediate, the faster the reaction proceeds, and the higher the yield of the desired product.

Hybridization and geometries also affect the properties of functional groups in organic compounds. For example, the sp2 hybridization state and trigonal planar geometry of the carbonyl group in aldehydes and ketones make them highly polar and reactive towards nucleophiles. The sp3 hybridization state and tetrahedral geometry of the alcohol functional group in alcohols make them less polar and less reactive than carbonyl compounds.

Applications in Materials Science

Hybridization and geometries are also essential in materials science because they affect the properties of materials, such as their mechanical strength, conductivity, and optical properties. For example, the sp2 hybridization state and planar geometry of graphene give it unique mechanical, electrical, and thermal properties, which make it a promising material for various applications, such as electronics, energy storage, and sensors.

The hybridization state and geometries of the atoms in a crystal lattice also determine the properties of materials. For example, diamond is a hard and transparent material because of the sp3 hybridization state and tetrahedral geometry of the carbon atoms in its crystal lattice. The sp2 hybridization state and planar geometry of the carbon atoms in graphite, on the other hand, give it a layered structure and high electrical conductivity.

Conclusion

In conclusion, hybridization and geometries are fundamental concepts in chemistry that describe the bonding and shape of molecules. These concepts are critical for understanding the properties and behavior of molecules in various chemical reactions and materials science. The study of hybridization and geometries has important applications in organic chemistry and materials science, such as the design of new drugs, catalysts, and materials with specific properties. The principles of hybridization and geometries will continue to be essential for advancing our understanding of the molecular world and developing new technologies in the future.

Exit mobile version