Circumscribed circle

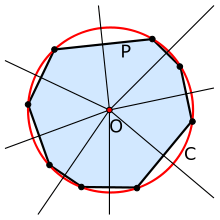
In calculation, the encompassed circle or circumcircle of a polygon is a circle that goes through all the vertices of the polygon. The focal point of this circle is known as the circumcenter and its range is known as the circumradius.

Few out of every odd polygon has an encompassed circle. A polygon that has one is known as a cyclic polygon, or once in a while a concyclic polygon in light of the fact that its vertices are concyclic. All triangles, all ordinary basic polygons, all square shapes, every isosceles trapezoid, and good kites are cyclic.

A connected thought is the one of a base bouncing circle, which is the littlest circle that totally holds the polygon inside it, assuming the circle’s middle is inside the polygon. Each polygon has an exceptional least jumping circle, which might be built by a direct time calculation. Regardless of whether a polygon has a delineated circle, it very well might be not quite the same as its base bouncing circle. For instance, for a harsh triangle, the base bouncing circle has the longest side as measurement and doesn’t go through the contrary vertex.

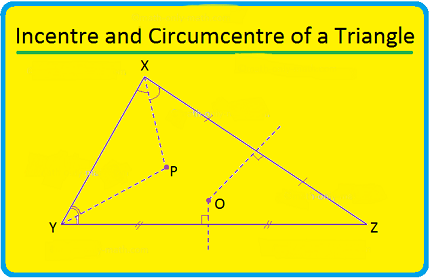
Incenter

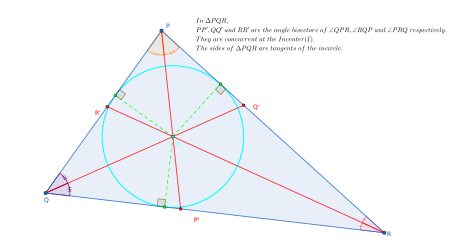
In math, the incenter of a triangle is a triangle community, a point characterized for any triangle in a manner that is free of the triangle’s situation or scale. The incenter might be equally characterized as where the inward point bisectors of the triangle cross, as the point equidistant from the triangle’s sides, as the intersection point of the average pivot and deepest mark of the grassfire change of the triangle, and as the middle place of the engraved circle of the triangle.

Along with the centroid, circumcenter, and orthocenter, it is one of the four triangle communities known to the antiquated Greeks, and the only one of the four that doesn’t in that frame of mind on the Euler line. It is the primary recorded focus, X(1), in Clark Kimberling’s Reference book of Triangle Focuses, and the character component of the multiplicative gathering of triangle focuses.

For polygons with multiple sides, the incenter just exists for digressive polygons – those that have an incircle that is digression to each side of the polygon. For this situation the incenter is the focal point of this circle and is similarly far off from all sides.

Triangle center

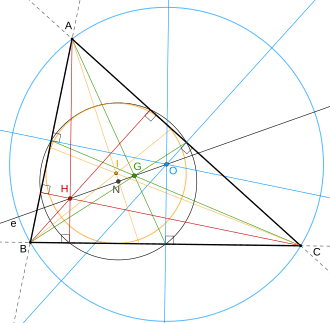
In math, a triangle place or triangle focus is a point in the triangle’s plane that is in some sense in the triangle. For instance, the centroid, circumcenter, incenter and orthocenter were recognizable to the old Greeks, and can be gotten by straightforward developments.

Every one of these traditional focuses has the property that it is invariant (all the more definitively equivariant) under comparability changes. All in all, for any triangle and any likeness change (like a revolution, reflection, expansion, or interpretation), the focal point of the changed triangle is a similar point as the changed focus of the first triangle. This invariance is the characterizing property of a triangle community. It precludes other notable focuses, for example, the Brocard focuses which are not invariant under reflection thus neglect to qualify as triangle focuses.

For a symmetrical triangle, all triangle communities match at its centroid. Anyway the triangle habitats for the most part take various situations from one another on any remaining triangles. The definitions and properties of thousands of triangle focuses have been gathered in the Reference book of Triangle Focuses.

What is Required Incentre of a triangle

The incenter of a triangle is the point where the three angle bisectors intersect. An angle bisector is a line that divides an angle into two equal angles.

The incenter is the center of the circle that is inscribed inside the triangle. This circle is called the inscribed circle or the incircle.

The incenter is equidistant from the three sides of the triangle. The distance from the incenter to a side of the triangle is called the inradius of the triangle.

The incenter plays an important role in geometry, as it is used to construct the incircle and to calculate various properties of the triangle, such as its area, perimeter, and angles.

What is Required circumcentre of a triangle

The circumcenter of a triangle is the point where the three perpendicular bisectors of the sides of the triangle intersect. A perpendicular bisector is a line that is perpendicular to a side of the triangle and passes through its midpoint.

The circumcenter is the center of the circle that passes through the three vertices of the triangle. This circle is called the circumcircle or the circumcenter.

The circumcenter is equidistant from the three vertices of the triangle. The distance from the circumcenter to a vertex of the triangle is called the circumradius of the triangle.

The circumcenter also plays an important role in geometry, as it is used to construct the circumcircle and to calculate various properties of the triangle, such as its area, perimeter, and angles. In addition, the circumcenter is the point where the perpendicular bisectors of the sides of the triangle intersect, which makes it useful for constructing and analyzing other geometric shapes.

How is Required Incentre of a triangle

The incentre of a triangle is the point where the angle bisectors of the triangle intersect. In other words, it is the center of the circle that is inscribed inside the triangle, touching all three sides.

To find the incentre of a triangle, follow these steps:

1. Draw the triangle and label the vertices as A, B, and C.
2. Draw the angle bisector of angle A. This is the line that divides angle A into two equal angles, and it intersects the opposite side BC at a point, which we’ll call D.
3. Repeat step 2 for angles B and C, and label the points of intersection with the opposite sides as E and F respectively.
4. The incentre of the triangle is the point where the three angle bisectors intersect. This is the point of concurrency of the three angle bisectors, and it can be found at the intersection of the lines AD, BE, and CF.

Alternatively, you can use the incentre formula, which gives the coordinates of the incentre as the weighted average of the coordinates of the three vertices of the triangle, where the weights are proportional to the lengths of the opposite sides. The formula is:

x = (axA + bxB + cxC)/(a + b + c) y = (ayA + byB + cyC)/(a + b + c)

where a, b, and c are the lengths of the sides of the triangle opposite the vertices A, B, and C respectively, and (xA, yA), (xB, yB), and (xC, yC) are the coordinates of the vertices A, B, and C respectively.

You can then use these coordinates to plot the incentre on a graph or to further analyze the triangle.

How is Required circumcentre of a triangle

The circumcentre of a triangle is the point where the perpendicular bisectors of the sides of the triangle intersect. In other words, it is the center of the circle that passes through all three vertices of the triangle.

To find the circumcentre of a triangle, follow these steps:

1. Draw the triangle and label the vertices as A, B, and C.
2. Find the midpoint of each side of the triangle. This can be done by taking the average of the x-coordinates and the y-coordinates of the two endpoints of the side.
3. Draw the perpendicular bisector of each side of the triangle. This can be done by constructing a line that passes through the midpoint of the side and is perpendicular to that side.
4. Find the point where two perpendicular bisectors intersect. This is the circumcentre of the triangle.

Alternatively, you can use the circumcenter formula, which gives the coordinates of the circumcentre as the intersection of the perpendicular bisectors of any two sides of the triangle. The formula is:

x = (a^2+b^2-c^2)/(2a) y = sqrt(b^2-x^2)

where a, b, and c are the lengths of the sides of the triangle opposite the vertices A, B, and C respectively.

You can then use these coordinates to plot the circumcentre on a graph or to further analyze the triangle.

Case Study on Incentre and circumcentre of a triangle

Suppose we have a triangle ABC with sides AB, BC, and AC. The incenter of the triangle is the point where the three angle bisectors of the triangle intersect, while the circumcenter is the point where the perpendicular bisectors of the three sides of the triangle intersect.

Let’s consider a specific example of a triangle ABC with the following coordinates:

A(0, 0) B(4, 0) C(0, 3)

To find the incenter, we first need to find the equations of the three angle bisectors. The angle bisector of angle A is the line that passes through A and bisects angle BAC. Let D be the point where this line intersects BC. Then we have:

BD/CD = AB/AC

Using the distance formula, we can find the coordinates of D:

BD^2 = (4 – x)^2 + y^2 CD^2 = x^2 + (3 – y)^2

Substituting into the above equation and simplifying, we get:

(x – 4/7)^2 + y^2 = 9/49

Thus, the equation of the angle bisector of angle A is:

x – 4/7 = +/- (3/7)sqrt((x – 4/7)^2 + y^2)

Similarly, we can find the equations of the angle bisectors of angles B and C. Solving the system of equations, we get the coordinates of the incenter:

I(2, 1)

To find the circumcenter, we first need to find the equations of the perpendicular bisectors of the three sides. The perpendicular bisector of AB is the line that passes through the midpoint of AB and is perpendicular to AB. Let E be the midpoint of AB with coordinates (2, 0). Then the equation of the perpendicular bisector of AB is:

x = 2

Similarly, we can find the equations of the perpendicular bisectors of BC and AC. Solving the system of equations, we get the coordinates of the circumcenter:

O(2, 3/2)

Therefore, the incenter of the triangle is at (2, 1) and the circumcenter is at (2, 3/2).

White paper on Incentre and circumcentre of a triangle

Introduction: The incenter and circumcenter of a triangle are two important points that are commonly used in geometry. They have unique properties that make them useful in solving various problems related to triangles. In this white paper, we will discuss the concept of incenter and circumcenter of a triangle, their properties, and their applications.

I. Incenter of a Triangle: The incenter of a triangle is the point where the three angle bisectors of the triangle intersect. It is denoted by the letter “I”. The angle bisector of an angle is a line that divides the angle into two equal parts. The incenter is the center of the inscribed circle of the triangle, which is the largest circle that can be drawn inside the triangle and touches all three sides.

Properties of Incenter:

1. The incenter is equidistant from the three sides of the triangle.
2. The incenter is the intersection of the angle bisectors of the triangle.
3. The incenter is the center of the inscribed circle of the triangle.

Applications of Incenter:

1. The incenter is used to find the radius of the inscribed circle.
2. The incenter is used to find the area of the triangle using the formula A = rs, where “r” is the radius of the inscribed circle and “s” is the semiperimeter of the triangle.
3. The incenter is used to find the distance between the incenter and any side of the triangle using the formula d = (2A)/(a+b+c), where “A” is the area of the triangle and “a”, “b”, and “c” are the lengths of the sides.

II. Circumcenter of a Triangle: The circumcenter of a triangle is the point where the perpendicular bisectors of the three sides of the triangle intersect. It is denoted by the letter “O”. The perpendicular bisector of a side is a line that passes through the midpoint of the side and is perpendicular to it. The circumcenter is the center of the circumcircle of the triangle, which is the smallest circle that can be drawn outside the triangle and touches all three vertices.

Properties of Circumcenter:

1. The circumcenter is equidistant from the three vertices of the triangle.
2. The circumcenter is the intersection of the perpendicular bisectors of the sides of the triangle.
3. The circumcenter is the center of the circumcircle of the triangle.

Applications of Circumcenter:

The circumcenter is the center of the circumcircle, which is a circle that passes through all the vertices of a triangle. Here are some applications of circumcenter:

1. Construction: The circumcenter can be used to construct the circumcircle of a triangle. This construction is useful in many areas of geometry.
2. Geometry: The circumcenter is a useful point in triangle geometry because it is equidistant from the three vertices of the triangle. This property can be used to prove theorems and solve problems involving triangles.
3. Navigation: The circumcenter can be used in navigation to determine the location of a ship or aircraft. By using triangulation, the circumcenter can be calculated to determine the position of the ship or aircraft.
4. Engineering: The circumcenter is used in engineering to determine the location of the center of gravity of an object. This can be useful in designing structures or vehicles.
5. Computer Graphics: The circumcenter is used in computer graphics to create 3D models of objects. By knowing the location of the circumcenter, the shape and size of an object can be accurately calculated.
6. Robotics: The circumcenter is used in robotics to determine the location of a robot in a 2D or 3D space. By using triangulation and the circumcenter, the position of the robot can be accurately calculated.
7. Physics: The circumcenter can be used in physics to determine the location of the center of mass of an object. This is useful in solving problems involving rotational motion and torque.

Conclusion:

In conclusion, the incentre and circumcentre are two important points associated with a triangle. The incentre is the center of the inscribed circle, which is the circle that touches all three sides of the triangle. The circumcentre, on the other hand, is the center of the circumcircle, which is the circle that passes through all three vertices of the triangle.

Both points have important geometric properties that are useful in various areas of mathematics and applied sciences. For example, the incentre is equidistant from all three sides of the triangle and can be used to solve problems involving the angle bisectors of a triangle, while the circumcentre is equidistant from all three vertices of the triangle and can be used to construct the circumcircle of a triangle, among other applications.

In general, understanding the properties and applications of these two points can deepen our understanding of the geometry of triangles and help us to solve a variety of mathematical and real-world problems.