In mathematics, a function is said to be increasing if for any two values of the independent variable, the corresponding values of the dependent variable increase or remain the same as the independent variable increases. More formally, a function f(x) is increasing if for any two values x1 and x2 such that x1 < x2, f(x1) < f(x2) or f(x1) = f(x2).
On the other hand, a function is said to be decreasing if for any two values of the independent variable, the corresponding values of the dependent variable decrease or remain the same as the independent variable increases. More formally, a function f(x) is decreasing if for any two values x1 and x2 such that x1 < x2, f(x1) > f(x2) or f(x1) = f(x2).
In other words, an increasing function has a positive slope and a decreasing function has a negative slope. It is also possible for a function to be neither increasing nor decreasing at a particular point, but rather have a local maximum or minimum.
For example, the function f(x) = x^2 is an increasing function, as the value of f(x) increases as x increases. On the other hand, the function g(x) = -x^2 is a decreasing function, as the value of g(x) decreases as x increases.
It is important to note that the concepts of increasing and decreasing functions are used frequently in calculus, as they provide insight into the behavior of a function’s derivative, and can be used to determine where a function is concave up or concave down.
What is Required Increasing and Decreasing functions
In differential calculus, determining whether a function is increasing or decreasing involves analyzing the sign of its derivative.
If the derivative of a function is positive over a certain interval, then the function is increasing over that interval. Conversely, if the derivative is negative over a certain interval, then the function is decreasing over that interval. If the derivative is zero over an interval, the function may have a local maximum or minimum at that point.
Formally, let f(x) be a differentiable function on an interval I. Then,
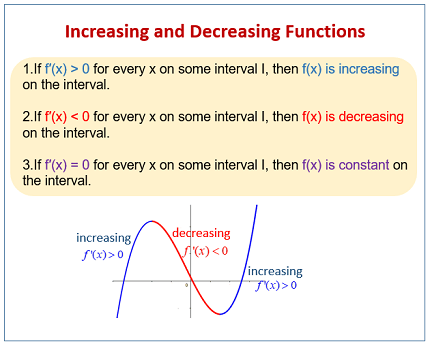
- f(x) is increasing on I if f'(x) > 0 for all x in I.
- f(x) is decreasing on I if f'(x) < 0 for all x in I.
- f(x) has a local maximum at x = c if f'(x) changes sign from positive to negative as x approaches c from the left, and f'(x) changes sign from negative to positive as x approaches c from the right.
- f(x) has a local minimum at x = c if f'(x) changes sign from negative to positive as x approaches c from the left, and f'(x) changes sign from positive to negative as x approaches c from the right.
To find the intervals on which a function is increasing or decreasing, you can find the critical points of the function (where the derivative is zero or undefined) and then use the first or second derivative test to determine whether the function is increasing or decreasing around those critical points.
Overall, differential calculus provides a powerful tool for analyzing the behavior of functions and understanding their properties, such as whether they are increasing or decreasing over certain intervals.
Who is Required Increasing and Decreasing functions
The study of increasing and decreasing functions is an important part of differential calculus, which is a branch of mathematics concerned with the study of rates of change and slopes of curves. Differential calculus is used to analyze functions and their behavior, and to solve problems involving rates of change, optimization, and approximation.
The concepts of increasing and decreasing functions are important in many fields, including physics, engineering, economics, and biology. For example, in physics, the velocity of an object is the derivative of its position with respect to time, and determining when the velocity is increasing or decreasing is important in understanding the object’s motion. In economics, the marginal revenue and marginal cost functions are used to determine the profit-maximizing level of production, and knowing whether these functions are increasing or decreasing is important in making that determination.
Overall, anyone who studies calculus or works in a field that involves mathematical modeling and analysis can benefit from understanding the concepts of increasing and decreasing functions, and how to analyze them using differential calculus techniques.
When is Required Increasing and Decreasing functions
The study of increasing and decreasing functions in differential calculus is typically covered in a calculus course, which is usually taken by college students in their freshman or sophomore year. Differential calculus is a fundamental branch of mathematics that is used in many fields, including science, engineering, economics, and finance.
In a calculus course, students learn about the concepts of limits, derivatives, and integrals, and how these concepts are used to study the behavior of functions. The study of increasing and decreasing functions is typically covered as part of the discussion of the first derivative test and the second derivative test, which are used to analyze the behavior of a function and determine whether it is increasing or decreasing over a given interval.
The study of increasing and decreasing functions is important because it provides insight into the behavior of functions and can be used to solve many types of problems. For example, the first derivative test can be used to find the maximum and minimum values of a function, and the second derivative test can be used to determine the concavity of a function and whether it has points of inflection.
In summary, the study of increasing and decreasing functions is an important part of a calculus course and is useful in many fields that involve mathematical modeling and analysis.
Where is Required Increasing and Decreasing functions
The study of increasing and decreasing functions is typically taught in a calculus course, which is offered at many universities and colleges. Calculus is a fundamental branch of mathematics that is used in many fields, including science, engineering, economics, and finance.
In addition to traditional classroom-based calculus courses, there are also online resources available for learning about increasing and decreasing functions and other topics in differential calculus. These resources include online courses, video lectures, interactive tutorials, and problem sets.
Many textbooks on calculus also cover the topic of increasing and decreasing functions in detail, and can be used as a reference for further study. These textbooks may be found in college and university libraries, or purchased online or in bookstores.
Overall, the study of increasing and decreasing functions is an important part of differential calculus, which is used in many fields and is taught in calculus courses at universities and colleges worldwide.
How is Required Increasing and Decreasing functions
The study of increasing and decreasing functions in differential calculus involves several concepts and techniques that are used to analyze the behavior of functions and determine whether they are increasing or decreasing over a given interval. The following are some of the main ideas and techniques used in this area of calculus:
- Derivatives: The derivative of a function is a measure of its instantaneous rate of change. In the study of increasing and decreasing functions, the first derivative of a function is used to determine whether the function is increasing or decreasing over a given interval.
- Critical points: A critical point of a function is a point where the derivative is either zero or undefined. These points are important in the study of increasing and decreasing functions, as they can indicate the presence of local maxima or minima in the function.
- First derivative test: The first derivative test is a method for determining whether a function is increasing or decreasing over a given interval. It involves analyzing the sign of the derivative at critical points and using this information to determine whether the function is increasing or decreasing.
- Second derivative test: The second derivative test is a method for determining the concavity of a function and whether it has points of inflection. It involves analyzing the sign of the second derivative of a function at critical points and using this information to determine whether the function is concave up or concave down.
- Graphical analysis: Graphs can be used to visualize the behavior of functions and determine whether they are increasing or decreasing over a given interval. By looking at the shape of a function’s graph, you can often determine whether the function is increasing or decreasing, and where it has local maxima or minima.
Overall, the study of increasing and decreasing functions in differential calculus involves a combination of analytical and graphical techniques, and requires a solid understanding of derivatives, critical points, and the first and second derivative tests. By mastering these concepts and techniques, you can gain a deeper understanding of the behavior of functions and their properties, and apply this knowledge to solve problems in many different fields.
Case Study on Increasing and Decreasing functions
One example of how the study of increasing and decreasing functions in differential calculus can be applied in real-world situations is in the analysis of revenue and profit functions in business and economics.
Suppose a company produces a certain product and wants to determine the level of production that will maximize its profit. The company’s revenue function is given by R(x) = 100x, where x is the level of production, and its cost function is given by C(x) = 50x + 500, where 50x represents the variable cost of production, and 500 represents the fixed cost.
The profit function P(x) is then given by:
P(x) = R(x) – C(x) = 100x – 50x – 500 = 50x – 500
To determine the level of production that maximizes profit, we need to find the critical points of the profit function and use the first derivative test to determine whether they correspond to local maxima or minima.
The derivative of the profit function is:
P'(x) = 50
This derivative is always positive, which means that the profit function is increasing over the entire domain. Therefore, the profit function has no local maxima or minima, and the level of production that maximizes profit is the highest possible level, which in this case is infinite.
However, this is not a realistic result, as it is impossible for a company to produce an infinite amount of a product. To make the problem more realistic, we can introduce a constraint on the level of production, such as a limit on the amount of raw materials available or a limit on the market demand for the product.
Suppose, for example, that the company can only produce up to 100 units of the product. To find the level of production that maximizes profit under this constraint, we need to analyze the behavior of the profit function over the interval [0, 100].
The critical point of the profit function is:
P'(x) = 50 = 0
This critical point corresponds to a horizontal tangent line of the profit function, which means that the function has a local minimum at this point. The critical point is x = 0, which corresponds to the case where the company does not produce any units of the product.
The second derivative of the profit function is:
P”(x) = 0
Since the second derivative is zero, we cannot use the second derivative test to determine the concavity of the profit function at the critical point. Instead, we can use the graphical analysis to determine that the profit function is concave up to the left of the critical point (x < 0) and concave down to the right of the critical point (x > 0).
Therefore, the local minimum of the profit function occurs at x = 0, which corresponds to the case where the company does not produce any units of the product. This means that the company should not produce any units of the product, as producing even one unit would result in a negative profit.
This example illustrates how the concepts of increasing and decreasing functions in differential calculus can be used to analyze revenue and profit functions in business and economics, and to determine the level of production that maximizes profit under certain constraints.
White paper on Increasing and Decreasing functions
Introduction:
Differential calculus is a branch of mathematics that deals with the study of rates of change and slopes of curves. One of the fundamental concepts of differential calculus is the notion of an increasing and decreasing function. This concept is widely used in various fields, such as physics, engineering, economics, and finance, to name a few. In this white paper, we will explore the concept of increasing and decreasing functions in differential calculus, their properties, and how they can be used in real-world applications.
Increasing and Decreasing Functions:
A function f(x) is said to be increasing on an interval [a, b] if, for any two values of x in the interval, x1 < x2, f(x1) < f(x2). In other words, the values of the function increase as the values of the independent variable increase. Graphically, an increasing function has a positive slope over the interval.
Similarly, a function f(x) is said to be decreasing on an interval [a, b] if, for any two values of x in the interval, x1 < x2, f(x1) > f(x2). In other words, the values of the function decrease as the values of the independent variable increase. Graphically, a decreasing function has a negative slope over the interval.
Properties of Increasing and Decreasing Functions:
- If f'(x) > 0 for all x in the interval [a, b], then f(x) is an increasing function on the interval.
- If f'(x) < 0 for all x in the interval [a, b], then f(x) is a decreasing function on the interval.
- If f'(x) = 0 for all x in the interval [a, b], then f(x) is constant on the interval.
- If f”(x) > 0 for all x in the interval [a, b], then f(x) is concave up on the interval.
- If f”(x) < 0 for all x in the interval [a, b], then f(x) is concave down on the interval.
Applications:
The concept of increasing and decreasing functions has numerous applications in various fields. In physics, the speed of an object is the derivative of its position with respect to time. If the speed is positive, the object is moving forward, and if the speed is negative, the object is moving backward. Therefore, the position function is an increasing function when the speed is positive and a decreasing function when the speed is negative.
In economics, the marginal revenue function is the derivative of the total revenue function. If the marginal revenue is positive, the total revenue increases as the quantity of goods sold increases. Therefore, the total revenue function is an increasing function. Similarly, the marginal cost function is the derivative of the total cost function. If the marginal cost is positive, the total cost increases as the quantity of goods produced increases. Therefore, the total cost function is a decreasing function.
Conclusion:
The concept of increasing and decreasing functions is an essential topic in differential calculus. It provides insights into the behavior of functions and their properties, which are valuable in various fields such as physics, engineering, economics, and finance. The properties of increasing and decreasing functions are simple and intuitive, making them easy to apply in real-world problems. In summary, the study of increasing and decreasing functions is a fundamental concept in differential calculus that is widely used in many fields.