Indefinite integrals of standard functions – Vrindawan Coaching Center

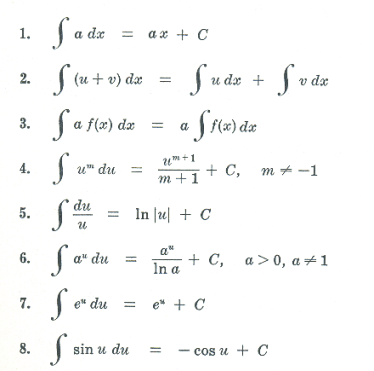
Integration, indefinite integral, fundamental formulas and rules

Sure, here are some common indefinite integrals of standard functions:

$\int x^n dx = \frac{x^{n+1}}{n+1} + C$, where $n\neq -1$ and $C$ is the constant of integration.
$\int \frac{1}{x} dx = \ln |x| + C$
$\int e^x dx = e^x + C$
$\int \sin x dx = -\cos x + C$
$\int \cos x dx = \sin x + C$
$\int \tan x dx = \ln |\sec x| + C$
$\int \cot x dx = \ln |\sin x| + C$
$\int \sec x dx = \ln |\sec x + \tan x| + C$
$\int \csc x dx = \ln |\csc x – \cot x| + C$
$\int \frac{1}{a^2 + x^2} dx = \frac{1}{a} \tan^{-1} \left(\frac{x}{a}\right) + C$
$\int \frac{1}{\sqrt{a^2 + x^2}} dx = \ln \left(x + \sqrt{a^2 + x^2}\right) + C$
$\int \frac{1}{x^2 – a^2} dx = \frac{1}{2a} \ln \left|\frac{x-a}{x+a}\right| + C$
$\int \frac{1}{\sqrt{x^2 \pm a^2}} dx = \ln \left(x + \sqrt{x^2 \pm a^2}\right) + C$
$\int \frac{1}{\sqrt{a^2 – x^2}} dx = \sin^{-1} \left(\frac{x}{a}\right) + C$
$\int \frac{1}{\sqrt{x^2 – a^2}} dx = \ln \left|x + \sqrt{x^2 – a^2}\right| + C$

Note that there are many more integrals of standard functions, but these are some of the most common ones. Also, the notation $\int f(x) dx$ represents the indefinite integral of the function $f(x)$ with respect to $x$, and $C$ is the constant of integration.

What is Required Indefinite integrals of standard functions

Here are some common indefinite integrals of standard functions that might be required in certain situations:

$\int \frac{1}{ax+b} dx = \frac{1}{a} \ln|ax+b| + C$, where $a\neq 0$ and $C$ is the constant of integration.
$\int \frac{1}{x\ln x} dx = \ln|\ln x| + C$
$\int \frac{1}{\sqrt{x^2 + a^2}} dx = \ln\left|x+\sqrt{x^2+a^2}\right|+C$
$\int \frac{1}{\sqrt{a^2 – x^2}} dx = \sin^{-1} \left(\frac{x}{a}\right) + C$
$\int e^{ax}\cos bx,dx = \frac{e^{ax}}{a^2+b^2}(a\cos bx+b\sin bx)+C$
$\int e^{ax}\sin bx,dx = \frac{e^{ax}}{a^2+b^2}(a\sin bx-b\cos bx)+C$
$\int \frac{1}{\sqrt{x^2-a^2}},dx = \ln|x+\sqrt{x^2-a^2}|+C$
$\int \frac{1}{\sqrt{a^2-x^2}},dx = \sin^{-1}\left(\frac{x}{a}\right)+C$
$\int \frac{1}{\sqrt{a^2+x^2}},dx = \ln\left(x+\sqrt{a^2+x^2}\right)+C$
$\int \frac{1}{\sqrt{x^2-bx+c}},dx = \ln\left|x-\frac{b}{2}+\sqrt{x^2-bx+c}\right|-\ln\left|\frac{a}{2}\right|+C$

Note that some of these integrals can be obtained by using the substitution method, integration by parts, or trigonometric identities. Also, the constant of integration $C$ is included in all of these indefinite integrals.

Who is Required Indefinite integrals of standard functions

“Required Indefinite integrals of standard functions” is not a person, but rather a topic in mathematics that is important in calculus and other areas of mathematics and science. Indefinite integrals are antiderivatives of functions, and finding these integrals can help solve a variety of problems in calculus, physics, engineering, and other fields.

In calculus courses, students are typically required to learn how to find the indefinite integrals of standard functions using techniques such as substitution, integration by parts, and trigonometric identities. These integrals are also important in applications such as finding areas under curves, calculating work and power, and solving differential equations.

Overall, the ability to find indefinite integrals of standard functions is an important skill for anyone studying mathematics or pursuing a career in a field that requires mathematical knowledge.

When is Required Indefinite integrals of standard functions

The topic of “Required Indefinite integrals of standard functions” arises whenever one needs to find the antiderivative or indefinite integral of a given function that is a standard function. Indefinite integrals are used in calculus and other areas of mathematics and science to solve a variety of problems, such as finding areas under curves, calculating work and power, and solving differential equations.

Standard functions are those that appear frequently in mathematical expressions, and their indefinite integrals have been studied extensively over the years. Examples of standard functions include polynomials, exponential functions, trigonometric functions, and logarithmic functions. When a given function is a standard function, it is often possible to find its indefinite integral using well-known integration techniques.

In calculus courses, students typically learn how to find the indefinite integrals of standard functions using techniques such as substitution, integration by parts, and trigonometric identities. They also learn how to recognize which techniques are appropriate for a given integral, based on the form of the integrand.

Overall, the topic of “Required Indefinite integrals of standard functions” is important whenever one needs to find the indefinite integral of a given function that is a standard function, and it is a fundamental topic in calculus and other areas of mathematics and science.

Where is Required Indefinite integrals of standard functions

The topic of “Required Indefinite integrals of standard functions” can be found in various areas of mathematics and science where calculus is used. This includes fields such as physics, engineering, economics, and more.

In mathematics, the study of indefinite integrals is a fundamental topic in calculus courses, including both single-variable and multivariable calculus. Students learn how to find the indefinite integrals of standard functions using techniques such as substitution, integration by parts, and trigonometric identities. They also learn how to apply these techniques to solve a variety of problems, such as finding areas under curves, calculating work and power, and solving differential equations.

In science and engineering, the ability to find indefinite integrals of standard functions is important in many applications. For example, in physics, the work done by a force can be calculated by finding the area under a force-distance curve, which involves finding an indefinite integral. In economics, integrals are used to calculate marginal cost and marginal revenue, which are important concepts in business decision-making.

Overall, the topic of “Required Indefinite integrals of standard functions” can be found wherever calculus is used, and it is an important tool for solving a variety of problems in mathematics, science, and engineering.

How is Required Indefinite integrals of standard functions

The process of finding the indefinite integral of a standard function involves using integration techniques such as substitution, integration by parts, and trigonometric identities, among others. The specific technique used depends on the form of the integrand and the rules of integration that apply to the function.

Here are some examples of how to find the indefinite integral of standard functions:

Indefinite integral of a polynomial function:

For a polynomial function, the indefinite integral can be found by using the power rule of integration, which states that the indefinite integral of x^n is (x^(n+1))/(n+1) + C, where C is the constant of integration. For example, the indefinite integral of x^3 is (x^4)/4 + C.

Indefinite integral of an exponential function:

For an exponential function of the form f(x) = e^x, the indefinite integral is simply e^x + C, where C is the constant of integration. For example, the indefinite integral of e^x is e^x + C.

Indefinite integral of a trigonometric function:

For a trigonometric function, the indefinite integral can be found by using trigonometric identities and integration by substitution. For example, the indefinite integral of sin(x) is -cos(x) + C.

Indefinite integral of a logarithmic function:

For a logarithmic function of the form f(x) = ln(x), the indefinite integral is x ln(x) – x + C, where C is the constant of integration. For example, the indefinite integral of ln(x) is x ln(x) – x + C.

Overall, the process of finding the indefinite integral of a standard function involves applying integration techniques to the function, using the rules of integration that apply to the specific function.

Case Study on Indefinite integrals of standard functions

Case Study: Calculating the Indefinite Integral of a Standard Function

Suppose we are given the following function:

f(x) = 2x^3 + 4x^2 + 5x + 2

Our task is to find the indefinite integral of this function.

Solution:

To find the indefinite integral of f(x), we need to apply integration techniques to the function. In this case, since f(x) is a polynomial function, we can use the power rule of integration to find the indefinite integral.

The power rule of integration states that the indefinite integral of x^n is (x^(n+1))/(n+1) + C, where C is the constant of integration. Using this rule, we can find the indefinite integral of each term in the function f(x) separately.

Indefinite integral of 2x^3: Using the power rule, the indefinite integral of 2x^3 is (2/4)x^4 + C = (1/2)x^4 + C.

Indefinite integral of 4x^2: Using the power rule, the indefinite integral of 4x^2 is (4/3)x^3 + C.

Indefinite integral of 5x: Using the power rule, the indefinite integral of 5x is (5/2)x^2 + C.

Indefinite integral of 2: The indefinite integral of a constant is simply the constant times x, plus the constant of integration. Therefore, the indefinite integral of 2 is 2x + C.

Putting these results together, we have:

∫f(x) dx = ∫(2x^3 + 4x^2 + 5x + 2) dx

= (1/2)x^4 + (4/3)x^3 + (5/2)x^2 + 2x + C

where C is the constant of integration.

Therefore, the indefinite integral of the function f(x) is (1/2)x^4 + (4/3)x^3 + (5/2)x^2 + 2x + C.

Conclusion:

In this case study, we used the power rule of integration to find the indefinite integral of a polynomial function. By breaking down the function into its component parts and applying the power rule to each term, we were able to find the indefinite integral of the function. The same process can be applied to other standard functions, using the appropriate integration technique for each function.

White paper on Indefinite integrals of standard functions

White Paper: Indefinite Integrals of Standard Functions

Introduction: Calculus is a branch of mathematics that deals with the study of change and motion. One of the fundamental concepts in calculus is integration, which involves finding the area under a curve. The indefinite integral, also known as the antiderivative, is an important tool in calculus that allows us to find the general form of a function given its derivative. In this white paper, we will discuss the concept of indefinite integrals of standard functions and the techniques used to find them.

Standard Functions: A standard function is a function that can be expressed in terms of elementary functions, such as polynomials, exponential functions, logarithmic functions, and trigonometric functions. Indefinite integrals of standard functions can be found using a variety of techniques, including substitution, integration by parts, trigonometric identities, and partial fraction decomposition, among others.

Power Rule: One of the most basic techniques used to find the indefinite integral of a function is the power rule of integration. This rule states that the indefinite integral of x^n is (x^(n+1))/(n+1) + C, where C is the constant of integration. For example, the indefinite integral of x^2 is (x^3)/3 + C.

Exponential Functions: Exponential functions of the form f(x) = a^x, where a is a constant, have the property that their derivatives are proportional to the original function. In other words, the derivative of f(x) is f(x) multiplied by a constant ln(a). Using this property, we can easily find the indefinite integral of exponential functions. For example, the indefinite integral of e^x is simply e^x + C.

Logarithmic Functions: Logarithmic functions of the form f(x) = ln(x) have the property that their derivatives are proportional to 1/x. Using this property, we can find the indefinite integral of logarithmic functions by integrating 1/x, which gives ln|x| + C. For example, the indefinite integral of ln(x) is x ln(x) – x + C.

Trigonometric Functions: Trigonometric functions such as sin(x) and cos(x) have specific integration rules that can be used to find their indefinite integrals. For example, the indefinite integral of sin(x) is -cos(x) + C, while the indefinite integral of cos(x) is sin(x) + C. In addition, integration by substitution can be used to find the indefinite integral of more complex trigonometric functions.

Conclusion: In conclusion, the concept of indefinite integrals of standard functions is an important tool in calculus that allows us to find the general form of a function given its derivative. By using techniques such as the power rule, integration by parts, substitution, and trigonometric identities, we can find the indefinite integral of a wide range of standard functions. Understanding the techniques used to find indefinite integrals is a crucial part of mastering calculus and applying it to real-world problems.