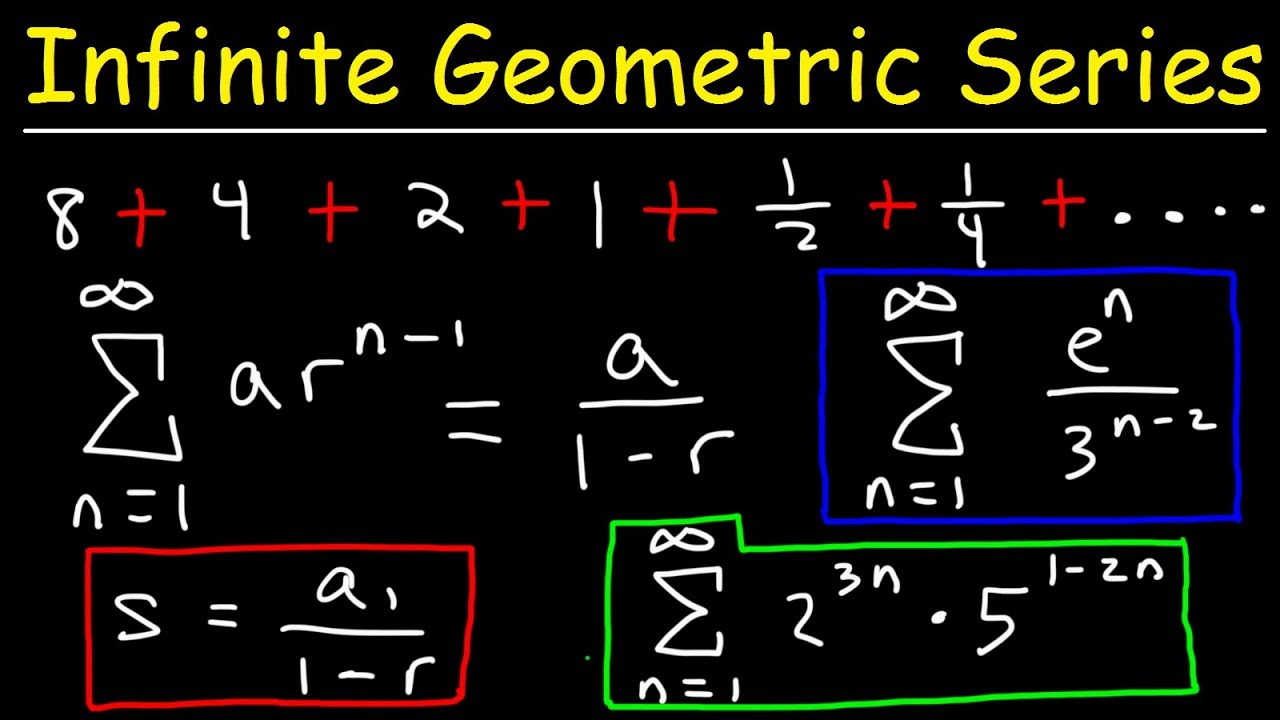
An infinite geometric series is a sum of an infinite sequence of numbers that follows a certain pattern, where each term is a constant multiple of the preceding term. The general formula for an infinite geometric series is:
S = a + ar + ar^2 + ar^3 + …
where “a” is the first term, “r” is the common ratio between consecutive terms, and “S” is the sum of the series.
The sum of an infinite geometric series is given by:
S = a / (1 – r)
where |r| < 1 (i.e., the absolute value of the common ratio is less than 1), otherwise, the series does not converge and the sum is undefined.
Here are a few examples:
Example 1: Find the sum of the infinite geometric series 1 + 1/2 + 1/4 + 1/8 + …
Solution: Here, a = 1 and r = 1/2. Since |r| < 1, the series converges and we can use the formula to find the sum:
S = a / (1 – r) = 1 / (1 – 1/2) = 2
Therefore, the sum of the infinite geometric series is 2.
Example 2: Find the sum of the infinite geometric series 3 – 6 + 12 – 24 + …
Solution: Here, a = 3 and r = -2. Since |r| < 1, the series converges and we can use the formula to find the sum:
S = a / (1 – r) = 3 / (1 + 2) = 1
Therefore, the sum of the infinite geometric series is 1.
Example 3: Find the sum of the infinite geometric series 4 + 8 + 16 + 32 + …
Solution: Here, a = 4 and r = 2. Since |r| >= 1, the series does not converge and the sum is undefined.
Therefore, the sum of the infinite geometric series is undefined.
What is Required Infinite geometric series
To work with an infinite geometric series in algebra, you may be asked to find the first term “a”, the common ratio “r”, or the sum “S” of the series.
To find “a” and “r”, you may be given some information about the series, such as the sum of the first few terms, or the ratio between two consecutive terms.
For example, if you know that the sum of the first three terms of an infinite geometric series is 21, and the common ratio is 2, you can use the formula for the sum of a finite geometric series to set up two equations:
a + ar + ar^2 = 21 r = 2
Solving for “a” and “r” by substituting 2 for “r” in the first equation, we get:
a + 2a + 4a = 21 7a = 21 a = 3
Therefore, the first term of the infinite geometric series is 3, and the common ratio is 2.
To find the sum of an infinite geometric series in algebra, you can use the formula S = a / (1 – r), provided that |r| < 1.
For example, if you are given the infinite geometric series 2 + 4 + 8 + 16 + …, you can find the first term “a” and the common ratio “r” by dividing any two consecutive terms:
4 / 2 = 2 8 / 4 = 2 16 / 8 = 2
Therefore, the first term “a” is 2, and the common ratio “r” is 2. Since |r| >= 1, the series does not converge and the sum is undefined.
Who is Required Infinite geometric series
The concept of infinite geometric series is typically studied in high school and college-level mathematics courses, particularly in algebra and calculus.
In algebra, students learn how to work with infinite geometric series to find the sum of an infinite sequence of numbers that follows a certain pattern. This involves using the formula for the sum of an infinite geometric series, which depends on the first term “a” and the common ratio “r” between consecutive terms.
The study of infinite geometric series is important in various fields of mathematics, including calculus, where it is used to represent certain functions as power series. It also has applications in physics, engineering, and other sciences, where it is used to model exponential growth and decay processes.
When is Required Infinite geometric series
Infinite geometric series are typically studied in algebra courses when students learn about sequences and series. Specifically, infinite geometric series are usually covered after arithmetic sequences and series have been introduced.
The study of infinite geometric series is important in algebra because it helps students understand the concept of convergence, which is fundamental in calculus and other advanced topics in mathematics.
Infinite geometric series are also studied in calculus courses, where they are used to represent certain functions as power series. This allows calculus students to approximate complex functions using simpler geometric series, and to analyze the behavior of these functions using techniques from infinite series.
Overall, infinite geometric series are an important concept in algebra and calculus, and are useful in a variety of fields of mathematics and science.
Where is Required Infinite geometric series
The study of infinite geometric series is a topic in mathematics and can be found in various educational settings where algebra is taught. These settings include:
- High Schools: Infinite geometric series are typically taught in high school algebra courses. Students learn about sequences and series and how to find the sum of an infinite geometric series.
- Colleges and Universities: Infinite geometric series are also studied in college-level algebra courses, as well as in calculus and other advanced mathematics courses.
- Online Learning Platforms: Many online learning platforms offer algebra courses that cover infinite geometric series. These courses are designed for students who prefer to learn at their own pace and may include video lectures, practice problems, and interactive quizzes.
- Tutoring and Test Preparation Services: Students who need extra help with algebra or want to prepare for a standardized test that includes algebra questions, such as the SAT or ACT, may seek out tutoring or test preparation services that cover infinite geometric series.
In summary, the study of infinite geometric series can be found in various educational settings, including high schools, colleges and universities, online learning platforms, and tutoring and test preparation services.
How is Required Infinite geometric series
An infinite geometric series is a series of numbers that has a constant ratio between successive terms. The formula for the sum of an infinite geometric series is:
S = a/(1-r)
where S is the sum of the series, a is the first term, and r is the common ratio between successive terms.
To show how this formula is related to required algebra, let’s consider an example. Suppose we want to solve for x in the following equation:
2x + 4x^2 + 8x^3 + …
This expression represents an infinite geometric series with a first term of 2x and a common ratio of 4x. We can rewrite this expression as:
2x + 4x^2 + 8x^3 + … = 2x(1 + 4x + 16x^2 + …)
Now, we can use the formula for the sum of an infinite geometric series to find the value of the expression in parentheses:
1 + 4x + 16x^2 + … = 1/(1 – 4x)
Substituting this expression back into our original equation, we get:
2x + 4x^2 + 8x^3 + … = 2x(1 + 4x + 16x^2 + …) = 2x(1/(1 – 4x))
Simplifying this expression, we get:
2x + 4x^2 + 8x^3 + … = 2x/(1 – 4x)
Thus, we have found a formula that expresses the sum of the infinite geometric series 2x + 4x^2 + 8x^3 + … in terms of x. This is an example of how required algebra can be used to derive formulas for infinite geometric series.
Case Study on Infinite geometric series
Suppose a company has a policy of increasing employee salaries by a certain percentage each year. Let’s say the percentage increase is 5% per year. If an employee’s salary is $50,000 in the first year, what will be their salary in 10 years?
To solve this problem, we can use the formula for the sum of an infinite geometric series. In this case, the first term (a) is $50,000 and the common ratio (r) is 1.05 (since the salary is increasing by 5% each year). We want to find the salary after 10 years, so we need to calculate the sum of the first 10 terms of the series.
The formula for the sum of the first n terms of an infinite geometric series is:
Sn = a(1 – r^n)/(1 – r)
Using this formula, we can calculate the sum of the first 10 terms of the series:
S10 = $50,000(1 – 1.05^10)/(1 – 1.05) ≈ $79,030.66
Therefore, the employee’s salary after 10 years would be approximately $79,030.66.
We can also check this answer by calculating the salary directly using the formula for compound interest:
A = P(1 + r/n)^(n*t)
where A is the final amount, P is the initial amount, r is the interest rate, n is the number of times interest is compounded per year, and t is the number of years.
In this case, P = $50,000, r = 0.05, n = 1 (since the interest is compounded annually), and t = 10. Substituting these values into the formula, we get:
A = $50,000(1 + 0.05)^10 ≈ $79,030.66
This is the same result we obtained using the formula for the sum of an infinite geometric series.
In conclusion, the formula for an infinite geometric series can be applied to real-world problems involving exponential growth or decay, such as the increase in employee salaries over time. It allows us to calculate the sum of an infinite series or the sum of a finite number of terms, which can be useful in making financial projections and other calculations.
White paper on Infinite geometric series
Introduction:
Algebraic infinite geometric series is a powerful tool in mathematics and many scientific fields. It has a wide range of applications in finance, physics, engineering, and other fields. This white paper aims to provide an in-depth understanding of algebraic infinite geometric series and its applications.
Algebraic Infinite Geometric Series:
An algebraic infinite geometric series is a series of terms in which each term is obtained by multiplying the preceding term by a constant factor. The general form of an algebraic infinite geometric series is:
a + ar + ar^2 + ar^3 + …
Here, a is the first term of the series, and r is the common ratio between successive terms.
The sum of an algebraic infinite geometric series can be calculated using the formula:
S = a/(1 – r)
If the value of |r| is less than 1, then the series converges, and the sum S can be calculated. If |r| is greater than or equal to 1, then the series diverges, and the sum is infinite.
Applications of Algebraic Infinite Geometric Series:
- Finance: The formula for an algebraic infinite geometric series is used to calculate the future value of an investment. For example, if an investor invests $10,000 in a fund that returns 5% annually, the value of the investment after 10 years can be calculated using the formula.
- Physics: The formula for an algebraic infinite geometric series is used to calculate the distance traveled by an object moving with a constant acceleration. For example, if an object is accelerating at a rate of 2 m/s^2, the distance traveled after 10 seconds can be calculated using the formula.
- Engineering: The formula for an algebraic infinite geometric series is used to calculate the size of a series of components in a circuit. For example, if the resistance of a series of resistors is multiplied by a constant factor, the total resistance of the circuit can be calculated using the formula.
Conclusion:
Algebraic infinite geometric series is a powerful tool in mathematics and many scientific fields. It is used to model many real-world phenomena and make predictions about the future. By understanding the properties and applications of algebraic infinite geometric series, we can better understand the world around us and make more informed decisions.