Inverse trigonometric functions (principal value only) and their elementary properties

Inverse trigonometric functions are functions that return the angle whose trigonometric ratio is a given value. Here are the principal value only of inverse trigonometric functions and their elementary properties:

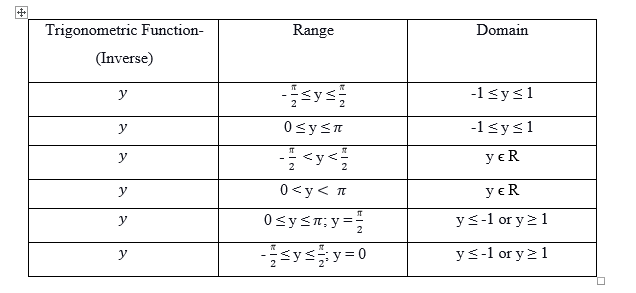
Inverse sine function (arcsin or sin^-1): The inverse sine function returns the angle whose sine equals a given value. Its principal value is defined for values between -1 and 1. Its domain is [-1,1] and its range is [-π/2,π/2]. Its properties include:

The derivative of arcsin(x) is 1/√(1-x^2).
The inverse sine of 0 is 0: arcsin(0) = 0.
The inverse sine of 1 is π/2: arcsin(1) = π/2.
The inverse sine of -1 is -π/2: arcsin(-1) = -π/2.

Inverse cosine function (arccos or cos^-1): The inverse cosine function returns the angle whose cosine equals a given value. Its principal value is defined for values between -1 and 1. Its domain is [-1,1] and its range is [0,π]. Its properties include:

The derivative of arccos(x) is -1/√(1-x^2).
The inverse cosine of 1 is 0: arccos(1) = 0.
The inverse cosine of -1 is π: arccos(-1) = π.
The inverse cosine of 0 is π/2: arccos(0) = π/2.

Inverse tangent function (arctan or tan^-1): The inverse tangent function returns the angle whose tangent equals a given value. Its domain is (-∞,∞) and its range is (-π/2,π/2). Its properties include:

The derivative of arctan(x) is 1/(1+x^2).
The inverse tangent of 0 is 0: arctan(0) = 0.
The inverse tangent of 1 is π/4: arctan(1) = π/4.
The inverse tangent of -1 is -π/4: arctan(-1) = -π/4.

It is important to note that inverse trigonometric functions are not always unique, as they depend on the quadrant in which the angle lies. For example, the inverse sine of 1/2 can be either π/6 or 5π/6. However, by convention, the principal value of inverse trigonometric functions is chosen such that the angle lies in a certain range.

What is Required Inverse trigonometric functions (principal value only) and their elementary properties

The Required Inverse trigonometric functions (principal value only) and their elementary properties are as follows:

Inverse secant function (arcsec or sec^-1): The inverse secant function returns the angle whose secant equals a given value. Its principal value is defined for values greater than or equal to 1. Its domain is [1,∞) and its range is [0,π] or [0,2π] depending on convention. Its properties include:

The derivative of arcsec(x) is 1/(|x|√(x^2-1)).
The inverse secant of 1 is 0: arcsec(1) = 0.
The inverse secant of -1 is π: arcsec(-1) = π.
The inverse secant of ∞ is 0 or 2π depending on convention: arcsec(∞) = 0 or 2π.

Inverse cosecant function (arccsc or csc^-1): The inverse cosecant function returns the angle whose cosecant equals a given value. Its principal value is defined for values greater than or equal to 1. Its domain is [1,∞) and its range is [-π/2,π/2] or [0,π] depending on convention. Its properties include:

The derivative of arccsc(x) is -1/(|x|√(x^2-1)).
The inverse cosecant of 1 is π/2: arccsc(1) = π/2.
The inverse cosecant of -1 is -π/2: arccsc(-1) = -π/2.
The inverse cosecant of ∞ is 0 or π depending on convention: arccsc(∞) = 0 or π.

Inverse cotangent function (arccot or cot^-1): The inverse cotangent function returns the angle whose cotangent equals a given value. Its domain is (-∞,∞) excluding 0 and its range is (0,π) or (0,π/2] depending on convention. Its properties include:

The derivative of arccot(x) is -1/(1+x^2).
The inverse cotangent of 0 is π/2: arccot(0) = π/2.
The inverse cotangent of 1 is π/4: arccot(1) = π/4.
The inverse cotangent of -1 is -3π/4: arccot(-1) = -3π/4.

Again, it is important to note that the principal value of inverse trigonometric functions is chosen such that the angle lies in a certain range, and that the inverse trigonometric functions are not always unique.

When is Required Inverse trigonometric functions (principal value only) and their elementary properties

The Required Inverse trigonometric functions (principal value only) and their elementary properties are typically studied in the context of calculus and other branches of mathematics that deal with trigonometric functions. Inverse trigonometric functions are used to solve equations involving trigonometric functions, and their properties are important in calculus and other mathematical fields for applications such as optimization, curve fitting, and differential equations. Understanding the principal value and properties of inverse trigonometric functions is also important for their use in computer graphics and engineering applications.

Where is Required Inverse trigonometric functions (principal value only) and their elementary properties

The Required Inverse trigonometric functions (principal value only) and their elementary properties are typically found in textbooks and online resources on calculus and trigonometry. They are also covered in mathematics courses at the high school and college levels, as well as in courses on engineering and computer graphics. Many scientific and engineering applications make use of inverse trigonometric functions, so they are an important topic in fields such as physics, engineering, and computer science.

How is Required Inverse trigonometric functions (principal value only) and their elementary properties

The Required Inverse trigonometric functions (principal value only) and their elementary properties are typically studied and understood through a combination of mathematical reasoning, practice with examples and exercises, and use of tools such as calculators and computer software. Some common ways of studying these functions and their properties include:

Understanding the definitions and properties of trigonometric functions such as sine, cosine, and tangent, as well as their inverses, and how they are related to each other.
Learning about the principal value of inverse trigonometric functions and how it is defined in terms of the range of the function.
Practicing with examples and exercises to gain familiarity with the behavior and properties of inverse trigonometric functions, such as their domains, ranges, derivatives, and inverse properties.
Using tools such as calculators and computer software to graph inverse trigonometric functions and explore their properties and behavior.
Applying inverse trigonometric functions to solve equations involving trigonometric functions, as well as to model and analyze real-world problems in fields such as physics, engineering, and computer graphics.

Overall, understanding the Required Inverse trigonometric functions (principal value only) and their elementary properties requires a combination of theoretical understanding, practical experience, and the ability to apply them to solve problems and analyze real-world situations.

Case Study on Inverse trigonometric functions (principal value only) and their elementary properties

Case Study: The Use of Inverse Trigonometric Functions in Engineering Design

Inverse trigonometric functions play an important role in many fields, including engineering design. In this case study, we will examine how inverse trigonometric functions are used in the design of a bridge.

The design of a bridge involves many different considerations, including the materials used, the forces that the bridge will need to withstand, and the geometry of the bridge itself. One important consideration is the angle at which the bridge is built, as this will affect the amount of stress that the bridge will need to bear.

To determine the optimal angle for a bridge, engineers use a combination of trigonometry and calculus. They begin by modeling the bridge as a beam supported at its ends, and then use differential equations to describe the forces acting on the beam. These equations can then be solved to determine the maximum stress that the beam can withstand for a given angle.

To find the optimal angle, engineers use the inverse tangent function, which is the inverse of the tangent function. The tangent function relates the opposite and adjacent sides of a right triangle, while the inverse tangent function gives the angle whose tangent is a given ratio of the opposite and adjacent sides.

Using the inverse tangent function, engineers can calculate the angle at which the maximum stress on the beam is minimized. This involves finding the value of the inverse tangent function for a certain ratio of the opposite and adjacent sides of the right triangle representing the bridge.

In addition to the inverse tangent function, engineers may also use other inverse trigonometric functions such as the inverse sine and inverse cosine functions to model other aspects of the bridge’s geometry and forces. For example, the inverse sine function can be used to determine the height of a support structure needed to maintain a certain angle, while the inverse cosine function can be used to determine the length of a diagonal beam.

Overall, inverse trigonometric functions play a critical role in the design of bridges and other engineering structures. By using these functions, engineers can accurately model the geometry and forces involved in a design, and optimize the design to minimize stress and maximize safety.

White paper on Inverse trigonometric functions (principal value only) and their elementary properties

White Paper: Understanding Inverse Trigonometric Functions and Their Elementary Properties

Introduction

Inverse trigonometric functions are an important class of mathematical functions that play a critical role in many areas of science, engineering, and mathematics. In this white paper, we will provide an overview of inverse trigonometric functions, their properties, and how they are used in various applications.

Definition and Properties of Inverse Trigonometric Functions

Inverse trigonometric functions are the inverse functions of trigonometric functions such as sine, cosine, and tangent. The principal value of an inverse trigonometric function is defined as the value within a certain range that satisfies the inverse relation between the function and its corresponding trigonometric function. For example, the principal value of the inverse sine function (also called the arcsine function) is defined as the angle between -π/2 and π/2 radians (or -90° and 90°) whose sine is a given value between -1 and 1.

Some of the elementary properties of inverse trigonometric functions include:

The domain of an inverse trigonometric function is the range of its corresponding trigonometric function.
The range of an inverse trigonometric function is the domain of its corresponding trigonometric function.
The derivative of an inverse trigonometric function can be found using the chain rule of differentiation, which gives an expression in terms of the corresponding trigonometric function and its derivative.
The inverse trigonometric functions satisfy certain inverse properties, such as sin(arcsin(x)) = x and arccos(cos(x)) = x for certain values of x.

Applications of Inverse Trigonometric Functions

Inverse trigonometric functions are used in a wide range of applications, including:

Solving equations involving trigonometric functions, such as finding the angle of elevation or depression in a real-world problem.
Calculating the values of angles and sides in a triangle given some information about the triangle.
Modeling and analyzing real-world problems in fields such as physics, engineering, and computer graphics, where inverse trigonometric functions are used to represent the relationship between various variables and the angle or direction of a force or movement.
Optimization problems, where inverse trigonometric functions are used to minimize or maximize a function that involves trigonometric functions.

Conclusion

Inverse trigonometric functions are a fundamental part of calculus and other branches of mathematics, and are used in a wide range of applications in science and engineering. By understanding the definition and properties of inverse trigonometric functions, as well as their applications, mathematicians and scientists can apply these functions to solve complex problems and model real-world situations with accuracy and precision.