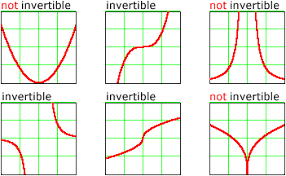
Invertible functions – Vrindawan Coaching Center

An invertible function is a function that has an inverse function. In other words, a function f(x) is invertible if and only if there exists another function g(x) such that g(f(x))=x for all x in the domain of f.

Invertible functions have a number of important properties. For example, they are one-to-one, meaning that no two distinct inputs have the same output. This is because if two distinct inputs had the same output, then the inverse function wouldn’t be well-defined.

Another important property of invertible functions is that their graphs are symmetric about the line y=x. This is because the inverse function is obtained by reflecting the graph of the original function about the line y=x.

Examples of invertible functions include the logarithmic function f(x) = log(base a)(x), where a is any positive number greater than 1, and the exponential function f(x) = a^x, where a is any positive number not equal to 1. These functions are inverses of each other, meaning that g(f(x))=x and f(g(x))=x for all x in the appropriate domains.

It’s worth noting that not all functions are invertible. For example, the function f(x) = x^2 is not invertible because it is not one-to-one – for any positive value of x, both x and -x have the same output, x^2.

Inverse function

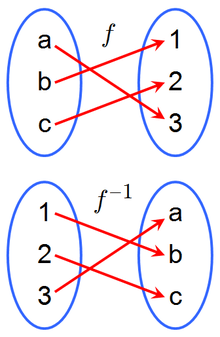
In mathematics, the inverse function of a function f (also called the inverse of f) is a function that undoes the operation of f. The inverse of f exists if and only if f is bijective, and if it exists, is denoted by $f^{-1}.$

For a function $f\colon X\to Y$ , its inverse $f^{-1}\colon Y\to X$ admits an explicit description: it sends each element ∈ $y\in Y$ to the unique element ∈ $x\in X$ such that f(x) = y.

As an example, consider the real-valued function of a real variable given by f(x) = 5x − 7. One can think of f as the function which multiplies its input by 5 then subtracts 7 from the result. To undo this, one adds 7 to the input, then divides the result by 5. Therefore, the inverse of f is the function

$f^{-1}\colon \mathbb {R} \to \mathbb {R}$ defined by $f^{-1}(y)={\frac {y+7}{5}}.$

Inverse function theorem

In math, explicitly differential analytics, the converse capability hypothesis gives an adequate condition for a capability to be invertible in a neighborhood of a point in its space: to be specific, that its subordinate is persistent and non-zero at the point. The hypothesis likewise gives a recipe for the subsidiary of the reverse capability. In multivariable math, this hypothesis can be summed up to any persistently differentiable, vector-esteemed capability whose Jacobian determinant is nonzero at a point in its space, giving an equation for the Jacobian network of the backwards. There are likewise variants of the backwards capability hypothesis for complex holomorphic capabilities, for differentiable guides between manifolds, for differentiable capabilities between Banach spaces, etc.

The hypothesis was first settled by Picard and Goursat utilizing an iterative plan: the essential thought is to make a decent statement hypothesis utilizing the compression planning hypothesis.

Inverse function rule

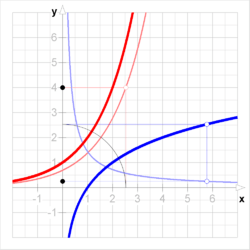
In calculus, the inverse function rule is a formula that expresses the derivative of the inverse of a bijective and differentiable function f in terms of the derivative of f. More precisely, if the inverse of $f$ is denoted as $f^{-1}$ , where $f^{-1}(y)=x$ if and only if $f(x)=y$ , then the inverse function rule is, in Lagrange’s notation,

$\left[f^{{-1}}\right]'(a)={\frac {1}{f'\left(f^{{-1}}(a)\right)}}$ .

This formula holds in general whenever $f$ is continuous and injective on an interval I, with $f$ being differentiable at $f^{-1}(a)$ ( $\in I$ ) and where $f'(f^{-1}(a))\neq 0$ . The same formula is also equivalent to the expression

${\mathcal {D}}\left[f^{-1}\right]={\frac {1}{({\mathcal {D}}f)\circ \left(f^{-1}\right)}},$

where ${\mathcal {D}}$ denotes the unary derivative operator (on the space of functions) and ∘ $\circ$ denotes function composition.

Geometrically, a function and inverse function have graphs that are reflections, in the line $y=x$ . This reflection operation turns the gradient of any line into its reciprocal.

Assuming that $f$ has an inverse in a neighbourhood of $x$ and that its derivative at that point is non-zero, its inverse is guaranteed to be differentiable at $x$ and have a derivative given by the above formula.

The inverse function rule may also be expressed in Leibniz’s notation. As that notation suggests,

${\frac {dx}{dy}}\,\cdot \,{\frac {dy}{dx}}=1.$

This relation is obtained by differentiating the equation $f^{-1}(y)=x$ in terms of x and applying the chain rule, yielding that:

${\frac {dx}{dy}}\,\cdot \,{\frac {dy}{dx}}={\frac {dx}{dx}}$

considering that the derivative of x with respect to x is 1.

Where is Required invertible functions

Invertible functions are useful in many areas of mathematics, science, and engineering. Some examples of where invertible functions are required include:

Cryptography: Invertible functions are used in cryptography to encrypt and decrypt messages. The encryption function is invertible, so the original message can be recovered by applying the decryption function.
Function composition: Invertible functions are important for function composition. If two functions are invertible, then their composition is also invertible, and the inverse of the composition is the composition of their inverses.
Optimization: Invertible functions are used in optimization problems, where the goal is to find the maximum or minimum of a function. In many cases, the function being optimized must be invertible in order to apply optimization techniques.
Physics: Invertible functions are used in many areas of physics, such as in the study of wave functions in quantum mechanics. The wave function must be invertible in order to calculate the probability density of a particle at a given location.
Engineering: Invertible functions are used in many engineering applications, such as control systems and signal processing. Invertible functions are used to model the behavior of systems and to design controllers that can manipulate the system to achieve desired outcomes.

These are just a few examples of where invertible functions are required. In general, invertible functions play an important role in many areas of mathematics, science, and engineering where the ability to recover original data or to manipulate systems in a controlled way is important.

How is Required invertible functions

Invertible functions are typically required in situations where there is a need to recover original data or to manipulate systems in a controlled way. In order to ensure that a function is invertible, it must satisfy certain conditions:

One-to-one: A function must be one-to-one in order to be invertible. This means that no two distinct inputs can have the same output. If two distinct inputs have the same output, then it is not possible to uniquely determine the original input from the output.
Onto: A function must also be onto in order to be invertible. This means that every element in the range of the function must have at least one pre-image in the domain of the function. If there are elements in the range of the function that do not have a pre-image, then it is not possible to recover the original data.
Continuous: A function must be continuous in order to be invertible. This means that small changes in the input result in small changes in the output. If a function is not continuous, then it may not be possible to recover the original data with sufficient accuracy.
Differentiable: A function must be differentiable in order to be invertible. This means that the function must have a well-defined derivative at every point in its domain. If a function is not differentiable, then it may not be possible to recover the original data using calculus-based methods.
Invertible itself: Finally, a function must be invertible itself. This means that there must exist another function that can recover the original data from the output of the function.

In general, ensuring that a function is invertible requires careful consideration of its properties and the context in which it will be used. Invertible functions are required in many areas of mathematics, science, and engineering where the ability to recover original data or to manipulate systems in a controlled way is important.

Case Study on invertible functions

Sure, here’s an example of a case study on invertible functions:

Suppose we have the function f(x) = 3x – 4. Our task is to determine if this function is invertible, and if so, find its inverse.

To determine if f(x) is invertible, we need to check if it passes the horizontal line test. The horizontal line test is a method of determining if a function is one-to-one, meaning that each input maps to a unique output. To perform the horizontal line test, we draw horizontal lines across the graph of the function. If the line intersects the graph at more than one point, then the function is not one-to-one and therefore not invertible.

Let’s graph f(x) = 3x – 4:

markdown
|
|   * (2, 2)
|     |
|     |
|     |
|   * | (0, -4)
|_____ _ _ _ _ x
     |
     |
     |
     |
     |

We can see that the graph of f(x) is a straight line with slope 3, passing through the point (0, -4). Since the line is not horizontal, it intersects the x-axis at exactly one point, which means that f(x) is one-to-one and therefore invertible.

To find the inverse of f(x), we need to solve for x in terms of y. Let y = 3x – 4:

y + 4 = 3x

x = (y + 4)/3

Thus, the inverse function of f(x) is g(y) = (y + 4)/3.

We can check that f(g(y)) = y and g(f(x)) = x, which confirms that f(x) and g(y) are indeed inverse functions:

f(g(y)) = f((y + 4)/3) = 3((y + 4)/3) – 4 = y

g(f(x)) = g(3x – 4) = (3x – 4 + 4)/3 = x

Therefore, the function f(x) = 3x – 4 is invertible, and its inverse is g(y) = (y + 4)/3.

White paper on invertible functions

Introduction:

In mathematics, an invertible function is a function that can be reversed or inverted. This means that for every output of the function, there exists a unique input that produced that output. Invertible functions are important in many areas of mathematics and computer science, including cryptography, data compression, and machine learning. In this white paper, we will explore invertible functions in detail, including their definition, properties, and applications.

Definition:

A function f: X → Y is invertible if and only if there exists a function g: Y → X such that g(f(x)) = x for all x in X, and f(g(y)) = y for all y in Y. In other words, if we apply f to x and then apply g to the result, we get back x, and if we apply g to y and then apply f to the result, we get back y. The function g is called the inverse function of f, and is denoted by f^(-1).

Properties:

An invertible function is bijective. This means that it is both injective (one-to-one) and surjective (onto).
The inverse of an invertible function is unique. That is, if f has an inverse function g, then g is unique.
If f and g are both invertible functions, then the composition of f and g is also invertible, and its inverse is given by (f ∘ g)^(-1) = g^(-1) ∘ f^(-1).
If f is an invertible function, then its inverse is also invertible, and its inverse is given by (f^(-1))^(-1) = f.

Applications:

Cryptography: Invertible functions are used in cryptography to encrypt and decrypt data. In particular, the RSA encryption algorithm uses invertible functions to generate public and private keys.
Data compression: Invertible functions are used in data compression to reduce the size of files without losing information. One example of an invertible compression algorithm is the Burrows-Wheeler transform.
Machine learning: Invertible functions are used in machine learning to transform data into a different representation that is easier to analyze. One example of an invertible transformation is the wavelet transform.

Conclusion:

Invertible functions are an important concept in mathematics and computer science. They have many applications in cryptography, data compression, and machine learning. Understanding the properties of invertible functions is essential for developing and implementing these applications.