Kirchhoff’s laws, also known as Kirchhoff’s circuit laws, are fundamental principles in electrical engineering and physics that describe the behavior of current and voltage in a closed circuit. There are two laws:
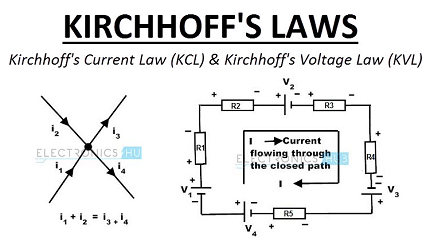
- Kirchhoff’s Current Law (KCL): This law states that the sum of all currents flowing into a node (or junction) in a circuit must be equal to the sum of all currents flowing out of that node. In other words, the total current entering a junction in a circuit must be equal to the total current leaving that junction.
Mathematically, KCL can be expressed as: Σ I = 0 where Σ I is the sum of all currents flowing into and out of a node.
- Kirchhoff’s Voltage Law (KVL): This law states that the sum of all voltage drops around a closed loop in a circuit must be equal to zero. In other words, the total voltage gained in a circuit loop must be equal to the total voltage lost in that same loop.
Mathematically, KVL can be expressed as: Σ V = 0 where Σ V is the sum of all voltage drops around a closed loop in a circuit.
These two laws are fundamental principles in electrical engineering and are used extensively in the analysis and design of electrical circuits.
What is Electricity and Magnetism Kirchhoff’s laws
Electricity and Magnetism are two closely related concepts in physics. Electricity deals with the flow of electric charge through conductors, while magnetism deals with the behavior of magnetic fields and their interactions with moving charges.
Kirchhoff’s laws are applicable to both electricity and magnetism. In electricity, Kirchhoff’s laws are used to analyze and design electrical circuits, while in magnetism, they are used to describe the behavior of magnetic fields and their interactions with currents.
Kirchhoff’s Current Law (KCL) states that the sum of currents entering a node (or junction) in a circuit must be equal to the sum of currents leaving that node. This law is based on the principle of conservation of charge, which states that the total charge in a closed system must remain constant. KCL is used to calculate the current in various branches of a circuit and to analyze the behavior of complex circuits.
Kirchhoff’s Voltage Law (KVL) states that the sum of voltages around a closed loop in a circuit must be equal to zero. This law is based on the principle of conservation of energy, which states that the total energy in a closed system must remain constant. KVL is used to calculate the voltage drops across various elements of a circuit and to analyze the behavior of complex circuits.
In magnetism, Kirchhoff’s laws are used to describe the behavior of magnetic fields and their interactions with currents. For example, Kirchhoff’s Voltage Law can be used to calculate the voltage induced in a coil by a changing magnetic field, while Kirchhoff’s Current Law can be used to calculate the current flowing in a loop of wire in the presence of a magnetic field.
Overall, Kirchhoff’s laws are fundamental principles in the study of electricity and magnetism, and are widely used in both theoretical and practical applications.
When is Electricity and Magnetism Kirchhoff’s laws
Kirchhoff’s laws are applicable whenever there is an electrical circuit or a system with currents and voltages that need to be analyzed. Kirchhoff’s laws are commonly used in the study of electricity and electronics, as well as in related fields such as telecommunications, control systems, and power engineering.
In the context of electricity, Kirchhoff’s laws are used to analyze circuits and to determine the current and voltage in different parts of the circuit. This is important in the design and optimization of circuits, as well as in troubleshooting and repair of faulty circuits. Kirchhoff’s laws are also used in the analysis of circuits containing resistors, capacitors, and inductors, as well as in more complex circuits containing diodes, transistors, and other components.
In the context of magnetism, Kirchhoff’s laws are used to describe the behavior of magnetic fields and their interactions with currents. This is important in the design and analysis of electrical machines such as motors and generators, as well as in the study of electromagnetic waves and other phenomena.
Overall, Kirchhoff’s laws are fundamental principles that are widely used in the study of electricity and magnetism, and are essential for understanding and designing electrical circuits and systems.
Where is Electricity and Magnetism Kirchhoff’s laws
Kirchhoff’s laws are a fundamental principle in the study of electricity and magnetism, and they can be applied to a wide variety of systems and devices that involve electrical currents and magnetic fields. These laws are widely used in the design and analysis of electrical circuits, electronic devices, and electromechanical systems.
Kirchhoff’s laws can be applied to a variety of situations and applications, such as:
- Electrical circuits: Kirchhoff’s laws are used to analyze and design circuits containing resistors, capacitors, and inductors. They can also be used in the analysis of more complex circuits containing diodes, transistors, and other components.
- Motors and generators: Kirchhoff’s laws are used to describe the behavior of magnetic fields and their interactions with currents in electrical machines such as motors and generators. This is important in the design and optimization of these devices.
- Telecommunications: Kirchhoff’s laws are used in the design and analysis of telecommunications systems, including circuits used in telephone networks, data transmission, and wireless communication.
- Power engineering: Kirchhoff’s laws are used in the analysis and design of power systems, including electrical grids, transformers, and power generation and distribution systems.
Overall, Kirchhoff’s laws are a fundamental concept in the study of electricity and magnetism, and they are essential for understanding and designing a wide range of electrical and electronic systems.
How is Electricity and Magnetism Kirchhoff’s laws
Kirchhoff’s laws are based on the fundamental principles of conservation of charge and conservation of energy. These laws describe the behavior of electrical currents and magnetic fields in a wide range of systems and devices.
Kirchhoff’s Current Law (KCL) states that the total current entering a node in a circuit must be equal to the total current leaving the node. This law is based on the principle of conservation of charge, which states that the total charge in a closed system must remain constant. KCL is used to calculate the current in various branches of a circuit and to analyze the behavior of complex circuits.
Kirchhoff’s Voltage Law (KVL) states that the sum of voltages around a closed loop in a circuit must be equal to zero. This law is based on the principle of conservation of energy, which states that the total energy in a closed system must remain constant. KVL is used to calculate the voltage drops across various elements of a circuit and to analyze the behavior of complex circuits.
These laws can be used in combination to analyze and design electrical circuits and systems. For example, KCL and KVL can be used to determine the voltage and current in different parts of a circuit, as well as to determine the power dissipated by different components in the circuit. Kirchhoff’s laws can also be used in the analysis of more complex systems, such as motors and generators, to determine the behavior of magnetic fields and electrical currents.
Overall, Kirchhoff’s laws provide a fundamental framework for understanding and analyzing the behavior of electrical currents and magnetic fields, and are essential for the design and optimization of a wide range of electrical and electronic systems.
Nomenclature of Electricity and Magnetism Kirchhoff’s laws
Kirchhoff’s laws are named after Gustav Kirchhoff, a German physicist who formulated these laws in the mid-19th century. There are two laws that are known as Kirchhoff’s laws: Kirchhoff’s Current Law (KCL) and Kirchhoff’s Voltage Law (KVL).
Kirchhoff’s Current Law (KCL) is also known as Kirchhoff’s first law or the node rule. KCL states that the sum of all currents entering a node or junction in a circuit must be equal to the sum of all currents leaving the node or junction. This law is expressed mathematically as:
Σi_in = Σi_out
Where Σi_in is the sum of all currents entering the node and Σi_out is the sum of all currents leaving the node.
Kirchhoff’s Voltage Law (KVL) is also known as Kirchhoff’s second law or the loop rule. KVL states that the algebraic sum of all voltage drops around any closed loop in a circuit must be zero. This law is expressed mathematically as:
ΣV = 0
Where ΣV is the algebraic sum of all voltage drops around the loop.
Overall, Kirchhoff’s laws provide a systematic and rigorous framework for analyzing electrical circuits and systems, and are essential for understanding and designing a wide range of electrical and electronic devices.
Case Study on Electricity and Magnetism Kirchhoff’s laws
One practical application of Kirchhoff’s laws is in the design and analysis of electrical circuits. In this case study, we will consider a simple circuit and use Kirchhoff’s laws to analyze its behavior.
Consider the circuit shown below, which consists of a voltage source (V), two resistors (R1 and R2), and two wires connecting the components.
+----R1----+
| |
V--+ +--R2--+
| | |
+----------+------+
We want to determine the current flowing through each resistor and the voltage drop across each resistor.
To analyze this circuit using Kirchhoff’s laws, we will apply KCL and KVL.
Applying KCL at the node between R1 and R2, we get:
I1 + I2 = I
Where I is the total current flowing through the circuit, I1 is the current flowing through R1, and I2 is the current flowing through R2.
Applying KVL around the loop containing the voltage source, R1, and R2, we get:
-V + IR1 + IR2 = 0
Where V is the voltage of the source, IR1 is the voltage drop across R1, and IR2 is the voltage drop across R2.
We can rewrite these equations as follows:
I1 + I2 = I
V = IR1 + IR2
We have two equations and two unknowns (I1 and I2), so we can solve for the currents.
Solving for I1 and I2, we get:
I1 = (V/R1) – (IR2/R1)
I2 = (IR2/R2)
Now we can calculate the voltage drops across each resistor:
VR1 = IR1 * R1 = V – IR2 * R2
VR2 = IR2 * R2
With these equations, we can calculate the current flowing through each resistor and the voltage drop across each resistor in the circuit.
Overall, this case study demonstrates how Kirchhoff’s laws can be applied to analyze the behavior of a simple electrical circuit. Kirchhoff’s laws provide a systematic and rigorous framework for analyzing electrical circuits and systems, and are essential for understanding and designing a wide range of electrical and electronic devices.
White paper on Electricity and Magnetism Kirchhoff’s laws
Introduction:
Electricity and Magnetism are two closely related phenomena that play a crucial role in the functioning of modern technology. Electrical circuits are used in a wide range of applications, from power generation and transmission to electronic devices such as computers and smartphones. To understand and analyze electrical circuits, it is essential to use Kirchhoff’s laws, which provide a systematic and rigorous framework for circuit analysis.
Kirchhoff’s Laws:
Kirchhoff’s laws are two fundamental principles that govern the behavior of electrical circuits. These laws were formulated by Gustav Kirchhoff, a German physicist, in the mid-19th century. The two laws are Kirchhoff’s Current Law (KCL) and Kirchhoff’s Voltage Law (KVL).
Kirchhoff’s Current Law (KCL):
KCL states that the sum of all currents entering a node or junction in a circuit must be equal to the sum of all currents leaving the node or junction. This law is based on the principle of conservation of charge, which states that the total amount of charge in a closed system is constant. KCL is also known as the node rule and is expressed mathematically as:
Σi_in = Σi_out
Where Σi_in is the sum of all currents entering the node and Σi_out is the sum of all currents leaving the node.
Kirchhoff’s Voltage Law (KVL):
KVL states that the algebraic sum of all voltage drops around any closed loop in a circuit must be zero. This law is based on the principle of conservation of energy, which states that the total energy in a closed system is constant. KVL is also known as the loop rule and is expressed mathematically as:
ΣV = 0
Where ΣV is the algebraic sum of all voltage drops around the loop.
Applications of Kirchhoff’s Laws:
Kirchhoff’s laws are essential for analyzing electrical circuits and systems. By applying KCL and KVL, we can determine the current flowing through each component in a circuit, the voltage drop across each component, and the overall behavior of the circuit. Kirchhoff’s laws are used in a wide range of applications, from power systems and electronics to telecommunications and control systems.
Conclusion:
In summary, Kirchhoff’s laws are two fundamental principles that govern the behavior of electrical circuits. KCL and KVL provide a systematic and rigorous framework for circuit analysis and are essential for understanding and designing a wide range of electrical and electronic devices. By using Kirchhoff’s laws, engineers and scientists can ensure the proper functioning of electrical circuits and systems and optimize their performance.