“Ideal solutions” typically refer to a concept in chemistry and thermodynamics where two or more substances mix together perfectly and form a homogeneous mixture where the intermolecular interactions between the components are the same as the intramolecular interactions within each component. In other words, the enthalpy of mixing is zero, and there are no attractive or repulsive forces between the molecules of the different components.

In practical terms, ideal solutions are rare, and most mixtures deviate from ideality to some extent due to differences in size, shape, polarity, and other properties of the molecules involved. However, ideal solutions are useful as a theoretical model for studying the behavior of real solutions and for predicting their properties under certain conditions.

In general, ideal solutions are characterized by several key features:

1. Complete mixing: The components mix together completely and form a homogeneous solution without any separation or phase change.
2. No energy change: There is no energy change or heat absorbed or released during the mixing process.
3. No volume change: The volume of the mixture is equal to the sum of the volumes of the components.
4. Raoult’s Law holds: The vapor pressure of each component in the mixture is proportional to its mole fraction in the mixture, as predicted by Raoult’s Law.
5. Ideal mixing entropy: The entropy change upon mixing is purely due to the increase in disorder or randomness and follows an ideal mixing entropy model.

Overall, ideal solutions are a useful theoretical concept that provides insight into the behavior of real solutions, even though they are rarely observed in practice.

What is Required ldeal solutions

“Required ideal solutions” is not a well-defined term in chemistry or thermodynamics. However, if you are referring to the conditions or criteria that are necessary for a mixture to behave ideally, then the following factors can be considered:

1. Similarity in molecular size and shape: The components of an ideal solution should have similar molecular sizes and shapes to ensure that the intermolecular interactions between the components are the same as the intramolecular interactions within each component.
2. Similarity in polarity: The components of an ideal solution should have similar polarities, so the attractive and repulsive forces between the molecules of the different components are balanced and do not deviate from ideality.
3. Low intermolecular forces: The intermolecular forces between the components should be weak and comparable in strength to the thermal energy of the system. This ensures that the molecules mix easily and do not form strong attractions or repulsions that would cause deviations from ideality.
4. Temperature and pressure: The temperature and pressure of the system should be within a certain range, depending on the components of the mixture, to ensure that the mixture is in a stable, homogeneous state and follows Raoult’s Law.
5. Dilute solutions: Ideal behavior is more likely to occur in dilute solutions, where the concentration of each component is relatively low, and the interactions between the molecules are minimized.

It is important to note that ideal solutions are rare and most mixtures deviate from ideality to some extent. Deviations from ideality can occur due to several factors, such as molecular size differences, polarity differences, and intermolecular forces, and can be characterized by activity coefficients that describe the extent of deviation from ideality.

Ideal gas

An ideal gas is a hypothetical gas made out of many haphazardly moving point particles that are not expose to interparticle communications. The ideal gas idea is helpful on the grounds that it submits to the best gas regulation, an improved on condition of state, and is managable to examination under factual mechanics. The prerequisite of zero connection can frequently be loose if, for instance, the communication is completely flexible or viewed as point-like impacts.

Under different states of temperature and tension, many genuine gases act subjectively like an ideal gas where the gas particles (or molecules for monatomic gas) assume the part of the best particles. Many gases, for example, nitrogen, oxygen, hydrogen, honorable gases, a few heavier gases like carbon dioxide and blends like air, can be treated as ideal gases inside sensible resistances over a significant boundary range around standard temperature and tension. By and large, a gas acts more like an ideal gas at higher temperature and lower pressure, as the expected energy because of intermolecular powers turns out to be less critical contrasted and the particles’ dynamic energy, and the size of the atoms turns out to be less huge contrasted with the vacant space between them. One mole of an ideal gas has a volume of 22.710947(13) liters at standard temperature and tension (a temperature of 273.15 K and a flat out strain of precisely 105 Dad) as characterized by IUPAC since 1982.[note 1]

The ideal gas model will in general fall flat at lower temperatures or higher tensions, when intermolecular powers and sub-atomic size becomes significant. It additionally falls flat for most weighty gases, like numerous refrigerants, and for gases areas of strength for with powers, remarkably water fume. At high tensions, the volume of a genuine gas is frequently extensively bigger than that of an optimal gas. At low temperatures, the tension of a genuine gas is frequently extensively not exactly that of an optimal gas. Eventually of low temperature and high strain, genuine gases go through a stage progress, for example, to a fluid or a strong. The model of an optimal gas, nonetheless, doesn’t portray or permit stage advances. These should be displayed by additional intricate conditions of state. The deviation from the ideal gas conduct can be depicted by a dimensionless amount, the compressibility factor, Z.

The ideal gas model has been investigated in both the Newtonian elements (as in “motor hypothesis”) and in quantum mechanics (as a “gas in a container”). The ideal gas model has likewise been utilized to demonstrate the way of behaving of electrons in a metal (in the Drude model and the free electron model), and it is quite possibly of the main model in factual mechanics.

In the event that the tension of an ideal gas is decreased in a choking cycle the temperature of the gas doesn’t change. (On the off chance that the strain of a genuine gas is diminished in a choking cycle, its temperature either decreases or rises, contingent upon whether its Joule-Thomson coefficient is positive or negative.)

Ideal and non-ideal solutions

Ideal Solutions:

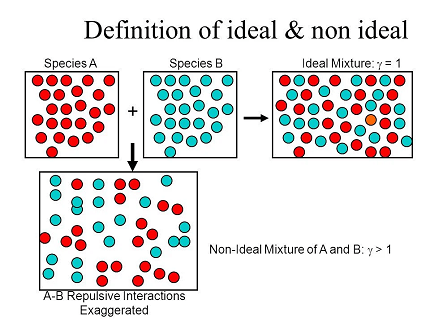
An ideal solution is a solution in which each component i.e. the solute as well as the solvent obeys the Raoult’s law over the entire range of concentration. Practically no solution is ideal over the entire range of concentration. However, when the concentration of solute is very low, the dilute solution behaves ideally. If the two components present in the solution (A and B) are identical in size, structure, and having almost similar intermolecular attractive forces between them (i.e. between A-A, B-B and B-A) and then the solution tends to behave like an ideal solution.

For an ideal solution

i) there is no change in the volume on mixing the two components (solute & solvents). (ΔV_mixing= 0)

ii) there is no exchange of heat when the solute is dissolved in solvent (ΔH_mixing = 0).

iii) escaping tendency of the solute and the solvent present in it should be same as in pure liquids.

Examples  for  ideal  solutions:  benzene & toluene; n-hexane & n-heptane; ethyl bromide &ethyl iodide; chlorobenzene & bromobenzene.

Non-ideal solutions

The solutions which do not obey Raoult’s law over the entire range of concentration, are called non-ideal solutions. For a non-ideal solution, there is a change in the volume and enthalpy upon mixing. i.e. ΔH_mixing ≠ 0 & ΔV_mixing ≠ 0. The deviation of the non-ideal solutions from the Raoult’s law can either be positive or negative.

Non-ideal solutions – positive deviation from Rauolt’s Law:

The nature of the deviation from the Rauolt’s law can be explained in terms of the intermolecular interactions between solute (A) and solvent (B). Consider a case in which the intermolecular attractive forces between A and B are weaker than those between the molecules of A (A-A) and molecules of B (B-B). The molecules present in such a solution have a greater tendency to escape from the solution when compared to the ideal solution formed by A and B, in which the intermolecular attractive forces (A-A, B-B, A-B) are almost similar. Consequently, the vapour pressure of such non-ideal solution increases and it is greater than the sum of the vapour pressure of A and B as predicted by the Raoult’s law. This type of deviation is called positive deviation.

Here, p_A > p°_A x_A and p_B > p°_B x_B

Hence p_total > p°_A x_A + p°_B x_B (9.19)

Let us understand the positive deviation by considering a solution of ethyl alcohol and water. In this solution the hydrogen bonding interaction between ethanol and water is weaker than those hydrogen bonding interactions amongst themselves (ethyl alcohol-ethyl alcohol and water-water interactions). This results in the increased evaporation of both components from the aqueous solution of ethanol. Consequently, the vapour pressure of the solution is greater than the vapour pressure predicted by Raoult’s law. Here, the mixing process is endothermic i.e. ΔH_mixing> 0 and there will be a slight increase in volume (ΔV_mixing> 0).

Examples for non-ideal solutions showing positive deviations: Ethyl alcohol & cyclohexane, Benzene & acetone, Carbon tetrachloride & chloroform, Acetone & ethyl alcohol, Ethyl alcohol & water.

Case Study on Ideal solutions

Here’s an example case study on ideal solutions:

Case Study: Ideal Solutions in Chemical Industry

In the chemical industry, the concept of ideal solutions plays a crucial role in designing and optimizing various processes involving mixtures of substances. One such example is the production of gasoline, where a mixture of hydrocarbons needs to be separated into different fractions based on their boiling points.

The ideal behavior of the gasoline mixture can be described using Raoult’s Law, which states that the vapor pressure of a component in a solution is proportional to its mole fraction. If the components of the gasoline mixture behaved ideally, the distillation process would be much simpler and more efficient.

However, in reality, most hydrocarbon mixtures do not behave ideally due to differences in molecular size, shape, and polarity, as well as the presence of impurities. Deviations from ideality can lead to poor separation efficiency, increased energy consumption, and reduced product quality.

To address these issues, chemical engineers use various techniques to enhance the ideal behavior of hydrocarbon mixtures. One such technique is the use of azeotropic distillation, where an entrainer is added to the mixture to form a new azeotrope that behaves more ideally and allows for better separation of the components.

Another technique is the use of zeolites, which are porous materials that can selectively adsorb certain molecules based on their size and polarity. By using zeolites as adsorbents or catalysts in various processes, engineers can achieve more selective and efficient separation of the components in a mixture.

Overall, the concept of ideal solutions plays a critical role in the chemical industry, and engineers must carefully consider and optimize the conditions that promote ideal behavior to ensure the efficient and effective production of high-quality products.

White paper on Ideal solutions

Here is a white paper on ideal solutions:

Introduction

Ideal solutions are a theoretical concept in chemistry and thermodynamics that describe the behavior of mixtures of substances that mix perfectly to form a homogeneous solution. In an ideal solution, the components of the mixture interact with each other in the same way they do with themselves, and the properties of the mixture are a simple weighted average of the properties of the individual components.

The concept of ideal solutions plays a crucial role in many areas of science and engineering, including chemical process design, material science, and biological systems. This white paper will provide an overview of ideal solutions, including their properties, characteristics, and applications.

Properties of Ideal Solutions

Ideal solutions have several unique properties that distinguish them from real solutions. The most important property of an ideal solution is that its vapor pressure follows Raoult’s Law. Raoult’s Law states that the partial vapor pressure of each component in a solution is proportional to its mole fraction in the mixture.

Another property of ideal solutions is that their enthalpy of mixing is zero. This means that no heat is either absorbed or released when the components of the mixture are mixed together.

Ideal solutions also have an ideal entropy of mixing, which means that the randomness of the mixture is the same as the randomness of the individual components. The ideal entropy of mixing is given by the equation:

ΔS_mix = -R[x_1 ln(x_1) + x_2 ln(x_2)]

where R is the gas constant, and x_1 and x_2 are the mole fractions of the two components in the mixture.

Characteristics of Ideal Solutions

Ideal solutions have several characteristics that make them idealized representations of real solutions. One characteristic is that the components of the mixture have similar molecular sizes and shapes, which ensures that the intermolecular interactions between the components are the same as the intramolecular interactions within each component.

Another characteristic of ideal solutions is that the components have similar polarities, so the attractive and repulsive forces between the molecules of the different components are balanced and do not deviate from ideality.

Ideal solutions also have low intermolecular forces between the components, which ensures that the molecules mix easily and do not form strong attractions or repulsions that would cause deviations from ideality.

Applications of Ideal Solutions

Ideal solutions have several important applications in science and engineering. One application is in the design and optimization of chemical processes involving mixtures of substances. For example, ideal solutions can be used to predict the behavior of mixtures in distillation, extraction, and other separation processes.

Another application of ideal solutions is in material science, where they can be used to design new materials with specific properties. For example, the ideal mixing behavior of some metal alloys can lead to the formation of unique crystal structures and physical properties.

Ideal solutions also have applications in biological systems, where they can be used to model the behavior of complex mixtures such as blood and other bodily fluids.

Conclusion

Ideal solutions are a powerful theoretical concept that has many applications in science and engineering. Their unique properties and characteristics make them idealized representations of real solutions, and they can be used to design and optimize chemical processes, create new materials, and model biological systems. While ideal solutions are rare in practice, understanding their behavior and properties can help scientists and engineers create more efficient and effective solutions to real-world problems.