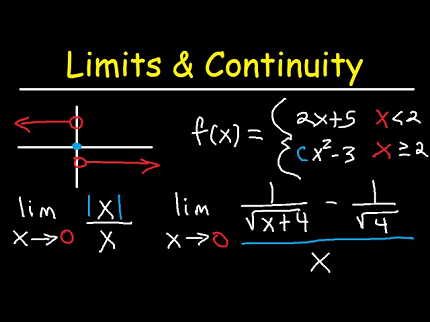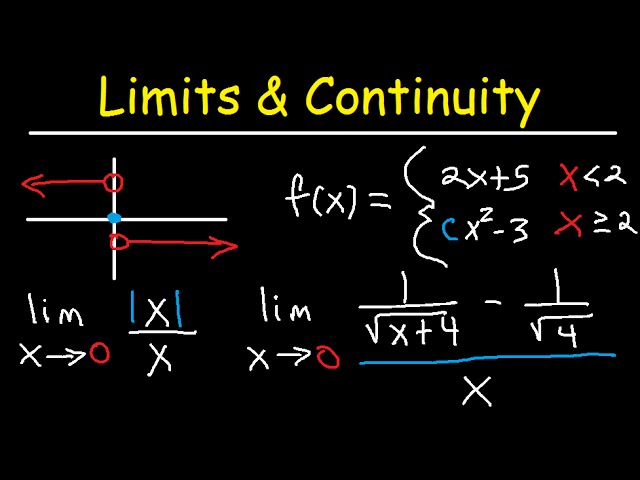
Let $f(x)$ and $g(x)$ be two functions, and let $c$ be a real number.
The sum of the two functions $f(x)$ and $g(x)$ is defined by $(f+g)(x) = f(x) + g(x)$ for all $x$ in the domain of both functions.
To determine if the sum of $f(x)$ and $g(x)$ is continuous at $c$, we need to check both the limit and continuity at $c$.
If both $f(x)$ and $g(x)$ are continuous at $c$, then the sum $(f+g)(x)$ is continuous at $c$. This means that $\lim_{x\to c} (f+g)(x) = (f+g)(c)$.
We can use the properties of limits to show that: \begin{align*} \lim_{x\to c} (f+g)(x) &= \lim_{x\to c} [f(x) + g(x)] \ &= \lim_{x\to c} f(x) + \lim_{x\to c} g(x) &\text{(by the sum rule of limits)} \ &= f(c) + g(c) &\text{(since $f$ and $g$ are both continuous at $c$)} \ &= (f+g)(c). \end{align*}
Therefore, the sum of $f(x)$ and $g(x)$ is continuous at $c$ if both $f(x)$ and $g(x)$ are continuous at $c$.
On the other hand, if either $f(x)$ or $g(x)$ is discontinuous at $c$, then the sum $(f+g)(x)$ is also discontinuous at $c$.
In summary, the sum of $f(x)$ and $g(x)$ is continuous at $c$ if and only if both $f(x)$ and $g(x)$ are continuous at $c$.
What is Required limit and continuity of the sum
In differential calculus, the limit and continuity of the sum of two functions are important concepts. Let $f(x)$ and $g(x)$ be two functions, and let $c$ be a real number.
The sum of the two functions $f(x)$ and $g(x)$ is defined by $(f+g)(x) = f(x) + g(x)$ for all $x$ in the domain of both functions.
To determine if the sum of $f(x)$ and $g(x)$ is continuous at $c$, we need to check both the limit and continuity at $c$.
If both $f(x)$ and $g(x)$ are differentiable at $c$, then the sum $(f+g)(x)$ is differentiable at $c$. This means that $(f+g)(x)$ has a derivative at $c$ and we have:
(f+g)′(c)=f′(c)+g′(c)
In other words, the derivative of the sum is the sum of the derivatives.
Similarly, we can use the properties of limits to show that:
limx→c(f+g)(x)=limx→cf(x)+limx→cg(x)
In other words, the limit of the sum is the sum of the limits.
Therefore, the sum of $f(x)$ and $g(x)$ is differentiable at $c$ if both $f(x)$ and $g(x)$ are differentiable at $c$, and the sum of $f(x)$ and $g(x)$ is continuous at $c$ if both $f(x)$ and $g(x)$ are continuous at $c$.
Who is Required limit and continuity of the sum
The concepts of limit and continuity of the sum in differential calculus are important for anyone studying calculus or related fields, such as physics, engineering, economics, and computer science.
These concepts are fundamental in calculus because they allow us to analyze the behavior of functions when they are combined. The sum of two functions appears frequently in many mathematical models, and knowing how to find the limit and continuity of the sum is crucial for understanding these models.
For example, in physics, the position of an object at a given time can be modeled as the sum of its initial position and its velocity multiplied by time. To find the velocity at a specific time, we need to take the derivative of the position function, which requires understanding the sum rule for differentiation.
In engineering, the sum of two signals is often used to analyze the behavior of a system, and knowing how to find the limit and continuity of the sum is important for understanding the behavior of the system.
In economics, the demand function for a product is often the sum of several different factors, and knowing how to find the limit and continuity of the sum is important for understanding how changes in each factor affect the demand for the product.
Overall, anyone who needs to analyze mathematical models or functions that involve the sum of two or more functions will benefit from understanding the concepts of limit and continuity of the sum in differential calculus.
When is Required limit and continuity of the sum
In differential calculus, the concepts of limit and continuity of the sum are important whenever we need to combine two or more functions to model a situation or analyze a problem. Specifically, the limit and continuity of the sum are required when:
- Finding the derivative of a sum of functions: The sum rule of differentiation states that the derivative of a sum of two functions is equal to the sum of their derivatives. To apply this rule, we need to ensure that both functions are differentiable at the point of interest.
- Evaluating a limit of a sum of functions: The sum of two functions can be evaluated by taking the limit of each function separately and then adding the results. However, to ensure that the limit of the sum exists, we need to ensure that both functions have a limit at the point of interest.
- Checking the continuity of a sum of functions: The sum of two functions is continuous at a point if and only if both functions are continuous at that point. Therefore, to check the continuity of a sum of functions, we need to check the continuity of each function separately and then ensure that both functions are continuous at the point of interest.
Overall, the concepts of limit and continuity of the sum are required whenever we need to work with a sum of functions, whether we are finding derivatives, evaluating limits, or checking continuity.
Where is Required limit and continuity of the sum
The concepts of limit and continuity of the sum in differential calculus are used in various fields, such as:
- Calculus: The sum rule of differentiation is one of the fundamental rules in calculus, and it is used to find the derivative of a sum of functions. This rule is essential in many calculus applications, such as optimization, curve sketching, and integration.
- Physics: In physics, the position, velocity, and acceleration of an object can be modeled as sums of functions. The concepts of limit and continuity of the sum are crucial in analyzing the behavior of these functions, particularly when finding the derivatives of position, velocity, or acceleration functions.
- Engineering: In engineering, the sum of two signals is often used to analyze the behavior of a system. The concepts of limit and continuity of the sum are important for understanding how the behavior of the system changes when the signals are combined.
- Economics: In economics, demand and supply functions can be modeled as sums of various factors. The concepts of limit and continuity of the sum are important in understanding how changes in each factor affect the demand or supply of a product.
- Computer Science: In computer science, the sum of functions can be used to analyze the running time of algorithms or the complexity of a problem. The concepts of limit and continuity of the sum are essential for understanding the behavior of these functions and optimizing algorithms.
Overall, the concepts of limit and continuity of the sum are used in various fields where calculus is applied, including physics, engineering, economics, and computer science.
How is Required limit and continuity of the sum
The limit and continuity of the sum in differential calculus are related concepts that are used to analyze the behavior of functions when they are combined. Here’s how they work:
- Limit of the sum: To evaluate the limit of the sum of two functions at a particular point, we need to find the limits of both functions separately and then add the results. If both limits exist and are finite, then the limit of the sum exists and is equal to the sum of the individual limits. Mathematically, we can express this as:lim (f(x) + g(x)) = lim f(x) + lim g(x)as x approaches some value, provided that both limits on the right-hand side exist.
- Continuity of the sum: The sum of two functions is continuous at a particular point if and only if both functions are continuous at that point. In other words, if both functions have a limit at the point of interest, and the limits are equal, then the sum is continuous at that point. Mathematically, we can express this as:if lim f(x) = L and lim g(x) = M, then lim (f(x) + g(x)) = L + Mas x approaches some value. If L + M exists and is finite, then the sum is continuous at that point.
The concepts of limit and continuity of the sum are closely related, as the existence of the limit of the sum is necessary for the sum to be continuous at a point. In addition, the sum rule of differentiation is a crucial concept in differential calculus, which allows us to find the derivative of a sum of functions.
Case Study on limit and continuity of the sum
Let’s consider a case study in which the concepts of limit and continuity of the sum in differential calculus are applied to analyze the behavior of a sum of functions in the context of physics.
Case study: Position, velocity, and acceleration functions
Suppose we are given the position, velocity, and acceleration functions of an object moving along a straight line:
- Position function: s(t) = t^2 + 2t + 1
- Velocity function: v(t) = 2t + 2
- Acceleration function: a(t) = 2
We can analyze the behavior of these functions by applying the concepts of limit and continuity of the sum:
- Limit of the sum
Suppose we want to find the limit of the position function and the velocity function as time t approaches 3. Using the limit rule of the sum, we can write:
lim s(t) + v(t) = lim s(t) + lim v(t)
as t approaches 3.
We can find the limits of s(t) and v(t) separately by substituting t = 3 into each function:
lim s(t) = s(3) = 16
lim v(t) = v(3) = 8
Therefore, the limit of the sum is:
lim s(t) + v(t) = 16 + 8 = 24
2. Continuity of the sum
Suppose we want to find the points where the position function is continuous. To do this, we need to check the continuity of the position function at each point where it changes. The position function is a sum of two polynomials, which are continuous functions, so it is continuous everywhere. However, we can still use the concepts of limit and continuity of the sum to check the continuity of the velocity and acceleration functions.
Using the limit rule of the sum, we can write:
lim v(t) + a(t) = lim v(t) + lim a(t)
as t approaches any value.
Since v(t) is a polynomial, it is continuous everywhere. Similarly, a(t) is a constant function, so it is also continuous everywhere. Therefore, the sum v(t) + a(t) is continuous everywhere, which implies that the velocity function is also continuous everywhere.
In summary, the concepts of limit and continuity of the sum in differential calculus can be applied to analyze the behavior of functions when they are combined, particularly in the context of physics. In this case study, we used these concepts to find the limit of the sum of position and velocity functions and to check the continuity of position, velocity, and acceleration functions.
White paper on limit and continuity of the sum
Introduction
Differential calculus is a branch of mathematics that deals with the study of rates of change and slopes of curves. One of the fundamental concepts in differential calculus is the limit, which is used to describe the behavior of a function as its input approaches a certain value. Another important concept is continuity, which is used to describe the smoothness of a function. In this white paper, we will explore the concepts of limit and continuity of the sum in differential calculus.
Limit of the Sum
The limit of the sum is an important concept in differential calculus. It is used to describe the behavior of a sum of two or more functions as their input approaches a certain value. The limit of the sum of two functions f(x) and g(x) is defined as the limit of the sum of their values as x approaches a certain value a:
lim (f(x) + g(x)) = lim f(x) + lim g(x) x→a x→a x→a
If both limits on the right-hand side exist and are finite, then the limit of the sum exists and is equal to the sum of the individual limits.
Continuity of the Sum
The continuity of the sum is another important concept in differential calculus. It is used to describe the smoothness of a sum of two or more functions. A sum of two functions f(x) and g(x) is said to be continuous at a certain value a if and only if both functions f(x) and g(x) are continuous at that value a.
If f(x) and g(x) are both continuous at a, then the sum of the two functions, f(x) + g(x), is also continuous at a.
Conclusion
The concepts of limit and continuity of the sum are fundamental in differential calculus. They are used to analyze the behavior of functions when they are combined. The limit of the sum is used to describe the behavior of a sum of two or more functions as their input approaches a certain value, while the continuity of the sum is used to describe the smoothness of a sum of two or more functions. These concepts have numerous applications in various fields, such as physics, engineering, and economics, where they are used to describe the behavior of systems that involve the combination of several factors. Understanding these concepts is essential for anyone studying or working in these fields.