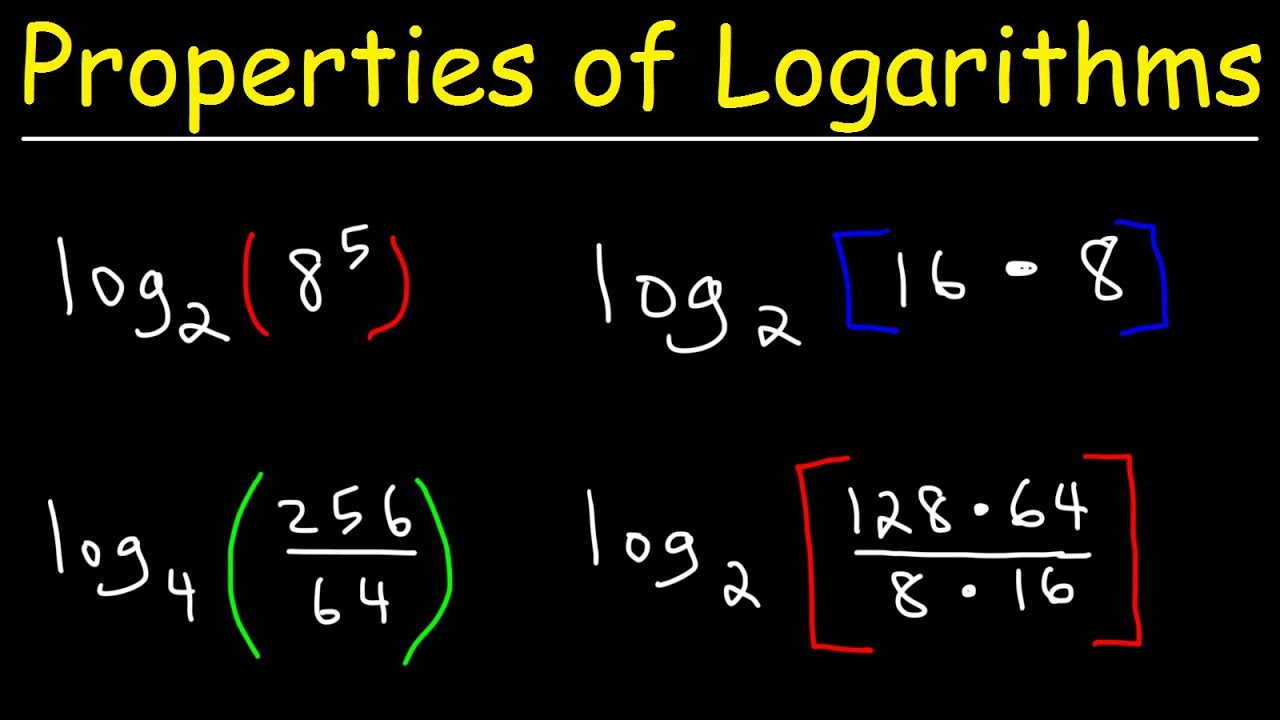
Logarithms are mathematical functions that are used to solve equations involving exponents. They are defined as the inverse of exponential functions. In other words, if we have an exponential function, a^x, the logarithm of that function, written as loga(x), is the exponent to which we raise the base a to get x.
The properties of logarithms are as follows:
- Product Property: loga(x*y) = loga(x) + loga(y) This property states that the logarithm of a product is equal to the sum of the logarithms of the individual factors.
- Quotient Property: loga(x/y) = loga(x) – loga(y) This property states that the logarithm of a quotient is equal to the difference of the logarithms of the individual factors.
- Power Property: loga(x^p) = p*loga(x) This property states that the logarithm of a power is equal to the product of the exponent and the logarithm of the base.
- Change of Base Property: logb(x) = loga(x)/loga(b) This property states that the logarithm of x with base b is equal to the logarithm of x with base a divided by the logarithm of b with base a.
- Logarithmic Identity Property: loga(a) = 1 This property states that the logarithm of the base with itself is always equal to 1.
- Logarithmic Inverse Property: a^loga(x) = x This property states that the exponential function with base a raised to the logarithm of x with base a is always equal to x.
These properties can be used to simplify logarithmic expressions, solve logarithmic equations, and manipulate exponential functions.
What is Required Logarithms and their properties
Algebra logarithms and their properties refer to the mathematical functions that are used to solve equations involving exponents. The following are the basic concepts and properties of algebra logarithms that are required:
- Definition of Logarithms: Understanding what logarithms are and their relationship with exponents.
- Logarithmic Properties: Knowing the different properties of logarithms, such as the product property, quotient property, power property, change of base property, logarithmic identity property, and logarithmic inverse property.
- Solving Logarithmic Equations: Knowing how to solve logarithmic equations using the properties of logarithms, such as simplifying the expressions, expanding or condensing logarithmic expressions, and solving for variables.
- Logarithmic Functions: Understanding the concept of logarithmic functions, including their graphs, domain and range, and inverse functions.
- Applications of Logarithms: Knowing how to apply logarithms in real-world situations, such as in finance, chemistry, biology, and physics.
Overall, a good understanding of algebra logarithms and their properties is essential for solving equations involving exponents, manipulating exponential functions, and analyzing real-world phenomena.
Who is Required Logarithms and their properties
Algebra logarithms and their properties are required for anyone who wants to study and understand higher level mathematics, such as calculus, differential equations, and advanced algebra. Specifically, the following individuals may benefit from having a strong understanding of algebra logarithms and their properties:
- High school and college students studying algebra, precalculus, and calculus.
- Mathematics majors and graduate students who are studying advanced algebra and calculus.
- Engineers, physicists, and scientists who use logarithmic functions in their work.
- Financial analysts and economists who work with interest rates and exponential growth.
- Computer scientists who work with algorithms and data analysis.
In short, anyone who wants to develop a strong foundation in mathematics, or who wants to work in a field that uses logarithmic functions, should have a solid understanding of algebra logarithms and their properties.
When is Required Logarithms and their properties
Algebra logarithms and their properties are required in various situations where exponential functions and equations are encountered. The following are some specific instances when algebra logarithms and their properties are used:
- Solving exponential equations: When solving equations that involve exponential functions, logarithms are used to simplify the equations and solve for the unknown variable.
- Compound interest and population growth: Logarithmic functions are used to model situations involving continuous growth or decay, such as compound interest or population growth.
- Acoustic decibels and pH levels: Logarithmic functions are used to measure and compare quantities that have a wide range of values, such as acoustic decibels or pH levels.
- Signal processing: Logarithms are used in signal processing to convert signals from linear to logarithmic scales, making them easier to process and analyze.
- Data analysis: Logarithmic functions are used in data analysis to normalize data with a wide range of values, such as in financial analysis or statistical analysis.
In summary, algebra logarithms and their properties are required whenever exponential functions and equations are encountered in various fields such as finance, science, engineering, and data analysis.
Where is Required Logarithms and their properties
Algebra logarithms and their properties are required in many fields where exponential functions and equations are encountered. Here are some specific areas where they are used:
- Mathematics: Algebra logarithms and their properties are used in higher-level mathematics such as calculus, complex analysis, and number theory.
- Science: Logarithms are used in various branches of science such as physics, chemistry, biology, and geology. They are used to model phenomena such as radioactive decay, population growth, and chemical reactions.
- Engineering: Logarithmic functions are used in engineering fields such as electrical engineering, civil engineering, and mechanical engineering. They are used to model systems involving exponential growth, decay, or damping.
- Finance: Logarithmic functions are used in finance to model compound interest, growth of investments, and amortization of loans.
- Computer science: Logarithmic functions are used in computer science to analyze algorithms and data structures.
Overall, algebra logarithms and their properties are required in many fields where exponential functions and equations are encountered. They are essential tools for modeling, analyzing, and understanding a wide range of phenomena in various disciplines.
How is Required Logarithms and their properties
Algebra logarithms and their properties are used in a variety of ways depending on the specific context and problem at hand. Here are some common ways they are used:
- Solving equations: Logarithmic properties are used to simplify equations involving exponential functions and solve for unknown variables. This involves using properties such as the product property, quotient property, and power property to manipulate the logarithmic expressions and isolate the unknown variable.
- Graphing functions: Logarithmic functions have unique properties that affect their graphs. For example, logarithmic functions are always increasing, but at a decreasing rate. Understanding these properties allows one to graph logarithmic functions accurately and identify important features such as intercepts, asymptotes, and domains and ranges.
- Modeling phenomena: Logarithmic functions are used to model a variety of phenomena in science, engineering, and finance. By understanding how to model these phenomena using logarithmic functions, we can make predictions about how they will behave in the future.
- Analyzing data: Logarithmic functions are used in data analysis to normalize data with a wide range of values. This allows us to compare and analyze data more easily and accurately.
- Converting between bases: The change of base property is used to convert logarithmic functions from one base to another. This is useful in situations where a different base is more convenient for analysis or computation.
Overall, algebra logarithms and their properties are used in various ways depending on the specific application. Understanding the properties and applications of logarithmic functions is essential for solving problems in many fields of study.
Case Study on Logarithms and their properties
Case Study: Using Algebra Logarithms and their Properties in Financial Analysis
In finance, logarithmic functions are commonly used to model compound interest, which is the interest earned on both the principal amount and any accumulated interest. The formula for calculating compound interest is:
A = P(1 + r/n)^(nt)
where A is the total amount, P is the principal amount, r is the annual interest rate, n is the number of times interest is compounded per year, and t is the number of years.
In some situations, we may need to solve for one of the variables in this equation, such as the interest rate, the principal amount, or the time. This is where algebra logarithms and their properties come into play.
Suppose we want to determine the interest rate required for an investment to double in 5 years, compounded annually. We can set up the equation as follows:
2P = P(1 + r/1)^(1*5)
where 2P is the amount after 5 years and P is the initial principal amount. We can simplify this equation by dividing both sides by P and taking the natural logarithm of both sides:
ln 2 = 5 ln(1 + r)
Using logarithmic properties, we can isolate r on one side of the equation:
ln(1 + r) = ln 2 / 5
We can then exponentiate both sides using the exponential function, e:
1 + r = e^(ln 2 / 5)
Solving for r, we get:
r = e^(ln 2 / 5) – 1
Using a calculator, we can evaluate this expression to get the required interest rate, which is approximately 0.035 or 3.5%.
This example demonstrates how algebra logarithms and their properties can be used to solve financial problems involving compound interest. By manipulating logarithmic expressions and applying properties such as the natural logarithm and exponential functions, we can solve for unknown variables and make informed financial decisions.
White paper on Logarithms and their properties
Introduction
Logarithms are mathematical functions that are widely used in various fields such as science, engineering, finance, and computer science. They are an essential tool for modeling, analyzing, and understanding phenomena involving exponential growth, decay, or damping. In this white paper, we will explore the properties of logarithmic functions and their applications in algebra.
Properties of Logarithmic Functions
- Definition: A logarithm is the inverse function of an exponential function. The logarithm of a number x with respect to a base b is the exponent to which b must be raised to obtain x. This can be written as:
log_b(x) = y
which is equivalent to:
b^y = x
- Logarithmic Laws:
There are several logarithmic laws that are used to manipulate logarithmic expressions. These laws include:
a. Product property: log_b(xy) = log_b(x) + log_b(y)
b. Quotient property: log_b(x/y) = log_b(x) – log_b(y)
c. Power property: log_b(x^y) = y log_b(x)
- Change of Base Property:
Sometimes it is necessary to change the base of a logarithmic expression. This can be done using the change of base property, which states that:
log_b(x) = log_a(x) / log_a(b)
where a and b are any two bases.
Applications of Logarithmic Functions in Algebra
- Solving Equations:
Logarithmic functions are often used to solve equations involving exponential functions. By using the logarithmic properties, we can manipulate the expressions to isolate the unknown variable.
- Graphing Functions:
Logarithmic functions have unique properties that affect their graphs. For example, logarithmic functions are always increasing, but at a decreasing rate. Understanding these properties allows one to graph logarithmic functions accurately and identify important features such as intercepts, asymptotes, and domains and ranges.
- Modeling Phenomena:
Logarithmic functions are used to model a variety of phenomena in science, engineering, and finance. By understanding how to model these phenomena using logarithmic functions, we can make predictions about how they will behave in the future.
- Analyzing Data:
Logarithmic functions are used in data analysis to normalize data with a wide range of values. This allows us to compare and analyze data more easily and accurately.
Conclusion
Algebra logarithms and their properties are essential tools for modeling, analyzing, and understanding a wide range of phenomena in various disciplines. They are required in many fields where exponential functions and equations are encountered. By understanding the properties and applications of logarithmic functions, we can solve problems in finance, science, engineering, and computer science, among other fields. The logarithmic functions play a critical role in mathematics, and they are used in many real-world applications.