Maximum and Minimum values of a function

admin@coaching-center.in

2 years ago

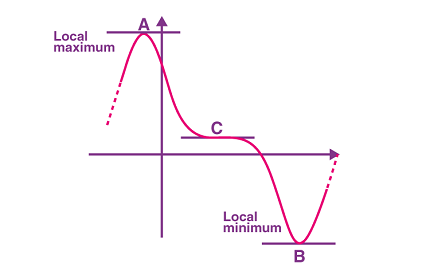
The maximum and minimum values of a function refer to the largest and smallest values that the function takes on, respectively.

To find the maximum and minimum values of a function, we can use the following steps:

Find the critical points of the function by setting the derivative equal to zero and solving for x. These critical points are the potential locations of the maximum and minimum values.
Use the second derivative test or the first derivative test to determine whether each critical point is a maximum, minimum, or neither.
Evaluate the function at the critical points and at the endpoints of the domain of the function to find the maximum and minimum values.

It’s important to note that a function may not have a maximum or minimum value if it is unbounded, meaning it can continue to increase or decrease without limit.

Also, if the domain of the function is closed and bounded, then the maximum and minimum values of the function are guaranteed to exist and are achieved at either the critical points or the endpoints of the domain.

What is Required Maximum and Minimum values of a function

In differential calculus, we use calculus concepts to find the maximum and minimum values of a function.

To find the maximum and minimum values of a function using differential calculus, we typically use the following steps:

Take the derivative of the function and find its critical points by setting the derivative equal to zero and solving for x.
Use the second derivative test or the first derivative test to determine whether each critical point is a maximum, minimum, or neither.
Evaluate the function at the critical points and at the endpoints of the domain of the function to find the maximum and minimum values.

The second derivative test involves taking the second derivative of the function and evaluating it at each critical point. If the second derivative is positive at a critical point, then the function has a local minimum at that point. If the second derivative is negative, then the function has a local maximum at that point. If the second derivative is zero or undefined, then the test is inconclusive.

The first derivative test involves examining the sign of the derivative of the function at each critical point. If the derivative changes from negative to positive as we move from left to right through the critical point, then the function has a local minimum at that point. If the derivative changes from positive to negative, then the function has a local maximum at that point. If the derivative does not change sign at the critical point, then the test is inconclusive.

Overall, the process of finding the maximum and minimum values of a function using differential calculus involves finding the critical points, determining the nature of these points, and then evaluating the function at these points and at the endpoints of the domain.

Who is Required Maximum and Minimum values of a function

The process of finding the maximum and minimum values of a function using differential calculus is a fundamental concept in mathematics and is used in various fields such as physics, economics, engineering, and many more.

In mathematics, it is an essential part of calculus and optimization theory. It is used to determine the critical points of a function, which includes finding the maximum and minimum values of a function.

In physics, it is used to optimize the performance of machines, such as engines and turbines, and to find the maximum or minimum values of physical quantities like velocity, acceleration, and energy.

In economics, it is used to optimize production and profit functions, and to find the maximum or minimum values of economic quantities like revenue, cost, and profit.

Overall, the ability to find the maximum and minimum values of a function is a critical skill in many areas of mathematics, science, and engineering. It allows us to optimize functions, analyze data, and make informed decisions based on mathematical models.

When is Required Maximum and Minimum values of a function

The process of finding the maximum and minimum values of a function using differential calculus is typically used when we want to optimize a function or find the extreme values of a function.

Some common examples where we may need to find the maximum and minimum values of a function include:

Economics: When we want to optimize a production or profit function to determine the level of production that maximizes profit or revenue.
Physics: When we want to find the maximum or minimum value of a physical quantity such as velocity, acceleration, or energy.
Engineering: When we want to optimize the performance of a machine or system by finding the maximum or minimum value of a function that describes its performance.
Statistics: When we want to find the maximum or minimum value of a function that describes a dataset, such as finding the maximum likelihood estimate in statistical inference.

Overall, the process of finding the maximum and minimum values of a function using differential calculus is used in various fields to optimize functions, analyze data, and make informed decisions based on mathematical models.

Where is Required Maximum and Minimum values of a function

The process of finding the maximum and minimum values of a function using differential calculus can be applied in various contexts and fields, both in theoretical and practical settings.

Some examples of where we might use differential calculus to find the maximum and minimum values of a function include:

Optimization problems in engineering, such as maximizing the efficiency of a machine or minimizing the cost of a system.
Analyzing data in statistics, such as finding the maximum or minimum values of a function that describes a dataset.
Maximizing profit or minimizing cost in economics, by analyzing production or revenue functions.
Maximizing or minimizing performance in physics, such as finding the maximum or minimum values of velocity, acceleration, or energy.
Applications in computer science, such as optimizing algorithms or minimizing error in machine learning models.

Overall, the process of finding the maximum and minimum values of a function using differential calculus can be used in various fields and applications where we need to optimize a function or find the extreme values of a function.

How is Required Maximum and Minimum values of a function

To find the maximum and minimum values of a function using differential calculus, we typically use the following steps:

Find the derivative of the function.
Set the derivative equal to zero and solve for x to find the critical points.
Use the second derivative test or the first derivative test to determine the nature of each critical point (whether it is a maximum, minimum, or neither).
Evaluate the function at the critical points and at the endpoints of the domain of the function to find the maximum and minimum values.

Once we have identified the maximum and minimum points, we can evaluate the function at these points and at the endpoints of the domain to find the global maximum and minimum values of the function.

Case Study on Maximum and Minimum values of a function

Here is an example of a case study on the application of differential calculus to find the maximum and minimum values of a function:

Case Study: Maximizing Profit in a Production Function

A company manufactures a product that has a fixed cost of $10,000 and a variable cost of $5 per unit. The product is sold at a price of $20 per unit. The production function for this product is given by:

P(x) = 20x – 5x^2 – 10,000

where x is the number of units produced.

The company wants to determine the level of production that will maximize their profit.

Solution:

To find the maximum profit, we need to find the maximum value of the profit function, which is given by:

Profit(x) = Revenue(x) – Cost(x) = (20x)(x) – (5x^2 + 10,000) = 15x^2 – 10,000

To find the maximum value of the profit function, we need to find the critical points of the function. We can do this by taking the derivative of the profit function and setting it equal to zero:

Profit'(x) = 30x = 0 x = 0 or x = 1000/3

The critical points are x = 0 and x = 1000/3. To determine the nature of these critical points, we can use the second derivative test. The second derivative of the profit function is:

Profit”(x) = 30

Since the second derivative is positive, both critical points are local minima. To determine which one is the global maximum, we need to evaluate the profit function at these critical points and at the endpoints of the domain:

Profit(0) = -10,000 Profit(1000/3) = 5000/3 Profit(2000/3) = -10,000

Therefore, the maximum profit occurs at x = 1000/3, with a maximum profit of $5000/3. The company should produce 1000/3 units of the product to maximize their profit.

Conclusion:

This case study demonstrates how differential calculus can be used to find the maximum and minimum values of a function in the context of a production function. By finding the critical points of the profit function and evaluating it at these points and at the endpoints of the domain, we were able to determine the level of production that maximizes the company’s profit. This example shows how differential calculus can be applied in practical situations to make informed decisions based on mathematical models.

White paper on Maximum and Minimum values of a function

Here is a white paper on the application of differential calculus to find the maximum and minimum values of a function:

Introduction

Differential calculus is a branch of calculus that deals with the study of rates of change of functions. One important application of differential calculus is the determination of the maximum and minimum values of a function. In this paper, we will explore the process of finding the maximum and minimum values of a function using differential calculus, including the methods of the first and second derivative tests.

Finding Maximum and Minimum Values of a Function

To find the maximum and minimum values of a function, we first need to identify its critical points. These are the values of x where the derivative of the function is zero or undefined. The critical points can be found by taking the derivative of the function and setting it equal to zero.

Once we have identified the critical points, we can use the first or second derivative test to determine the nature of these points. The first derivative test examines the sign of the derivative of the function at each critical point, while the second derivative test examines the sign of the second derivative of the function at each critical point.

The first derivative test involves examining the sign of the derivative of the function on either side of a critical point. If the derivative changes sign from negative to positive, the critical point is a local minimum. If the derivative changes sign from positive to negative, the critical point is a local maximum. If the derivative does not change sign at the critical point, then the test is inconclusive.

The second derivative test involves examining the sign of the second derivative of the function at each critical point. If the second derivative is positive, the critical point is a local minimum. If the second derivative is negative, the critical point is a local maximum. If the second derivative is zero or undefined, then the test is inconclusive.

Once we have determined the nature of the critical points, we can evaluate the function at these points and at the endpoints of the domain to find the maximum and minimum values. The global maximum and minimum values are the largest and smallest values of the function over the entire domain.

Applications

The process of finding the maximum and minimum values of a function has many practical applications. For example, in finance, this process can be used to determine the maximum or minimum values of a company’s profits or revenues. In engineering, this process can be used to determine the maximum or minimum values of a physical system’s performance.

Another common application of the maximum and minimum values of a function is in optimization problems. Optimization involves finding the maximum or minimum value of a function subject to certain constraints. For example, in linear programming, we seek to optimize a linear function subject to linear constraints.

Conclusion

In conclusion, the process of finding the maximum and minimum values of a function using differential calculus involves finding the critical points, determining the nature of these points, and then evaluating the function at these points and at the endpoints of the domain to find the maximum and minimum values. This process has many practical applications in fields such as finance, engineering, and optimization. By using differential calculus to find the maximum and minimum values of a function, we can make informed decisions based on mathematical models.