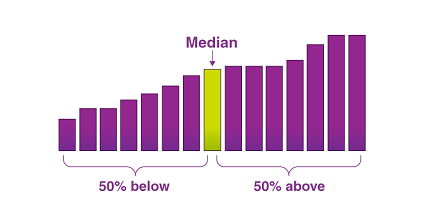
In probability and statistics, the median is a measure of central tendency that represents the middle value of a dataset when it is arranged in ascending or descending order.
To find the median of a dataset, you first need to arrange the values in order. If the dataset contains an odd number of values, the median is the middle value. For example, if you have the following dataset:
{2, 5, 7, 9, 12}
The median would be 7 because it is the middle value.
If the dataset contains an even number of values, the median is the average of the two middle values. For example, if you have the following dataset:
{2, 5, 7, 9, 12, 14}
The median would be (7+9)/2 = 8 because 7 and 9 are the middle values.
The median is a useful measure of central tendency because it is less affected by extreme values (outliers) than the mean.
What is Required Median
The Required Probability and Statistics Median refers to the median that is required or expected to be achieved in a specific situation, such as in a research study or a business decision-making process.
For example, in a clinical trial for a new drug, the required median might be the minimum level of improvement in the median response time that the drug needs to achieve to be considered effective. Or, in a marketing campaign, the required median might be the median level of sales that the company needs to achieve to break even or generate a profit.
In such cases, the required median is often determined based on specific criteria or benchmarks, such as previous research findings, industry standards, or financial goals. Statistical methods can be used to calculate the probability of achieving the required median, taking into account factors such as sample size, variability, and effect size.
The Required Probability and Statistics Median is important because it can help decision-makers set realistic goals and evaluate the success of their actions based on measurable outcomes.
Who is Required Median
“Required Probability and Statistics Median” is not a person or an individual. It is a statistical concept used to describe the minimum level of median or central tendency that is required or expected to be achieved in a specific situation, such as in a research study or a business decision-making process, as I explained in my previous answer.
The concept of Required Probability and Statistics Median is used in various fields, including science, medicine, finance, marketing, and engineering, to set goals, evaluate outcomes, and make informed decisions based on data and evidence.
When is Required Median
The Required Probability and Statistics Median is used in situations where a specific level of median or central tendency is required or expected to achieve a particular goal or meet certain criteria.
For example, in clinical trials, the Required Probability and Statistics Median might be used to determine the minimum level of improvement in the median response time that a new drug needs to achieve to be considered effective. In finance, the Required Probability and Statistics Median might be used to determine the median return on investment that is required to meet a specific financial goal. In marketing, the Required Probability and Statistics Median might be used to determine the median level of sales that is required to break even or generate a profit.
In general, the Required Probability and Statistics Median is used in situations where it is important to set specific goals, evaluate outcomes, and make informed decisions based on measurable outcomes. Statistical methods can be used to calculate the probability of achieving the Required Probability and Statistics Median, taking into account factors such as sample size, variability, and effect size.
Where is Required Median
The Required Probability and Statistics Median is not a physical location or a tangible object. It is a statistical concept used in various fields such as science, medicine, finance, marketing, and engineering to set goals, evaluate outcomes, and make informed decisions based on data and evidence.
The Required Probability and Statistics Median can be calculated and analyzed using statistical methods and software tools. These methods and tools can be applied to various types of data, including numerical, categorical, and ordinal data. The location where the analysis is performed can be anywhere with access to the necessary tools and data, such as a laboratory, a business office, or a research center.
In summary, the Required Probability and Statistics Median is a statistical concept that can be applied in various fields and analyzed using statistical methods and software tools. It is not associated with any specific physical location.
How is Required Median
The Required Probability and Statistics Median can be calculated and analyzed using statistical methods and software tools.
To calculate the Required Probability and Statistics Median, you first need to define the specific goal or criteria that you want to achieve. This goal or criteria may be based on previous research findings, industry standards, financial goals, or other factors.
Next, you need to determine the appropriate statistical method to calculate the median or central tendency that is required to achieve the goal or meet the criteria. This may involve calculating the sample size needed, determining the effect size, or using other statistical techniques.
Once you have determined the appropriate statistical method, you can apply it to your data to calculate the Required Probability and Statistics Median. This may involve using software tools such as Excel, SPSS, or R to perform the necessary calculations and statistical tests.
Finally, you can analyze the results of your calculations to determine the probability of achieving the Required Probability and Statistics Median, taking into account factors such as sample size, variability, and effect size. This analysis can help you make informed decisions and set realistic goals based on measurable outcomes.
Case Study on Median
Case Study:
A pharmaceutical company has developed a new drug to treat a specific medical condition. The company wants to conduct a clinical trial to test the effectiveness of the drug compared to the existing standard treatment. The primary outcome measure for the trial is the median time to response, which is defined as the time from the start of treatment to a specific level of improvement in the patient’s condition.
The company has set a Required Probability and Statistics Median of 50% improvement in the median time to response for the new drug compared to the standard treatment. This means that the median time to response for the new drug needs to be at least 50% lower than the median time to response for the standard treatment to be considered effective.
To achieve this goal, the company designs a randomized controlled trial involving 200 patients with the medical condition. The patients are randomly assigned to receive either the new drug or the standard treatment. The primary outcome measure, the median time to response, is recorded for each patient.
The data is analyzed using statistical methods, and the median time to response is calculated for each treatment group. The results show that the median time to response for the new drug group is 20 days, while the median time to response for the standard treatment group is 40 days.
To determine if the new drug has achieved the Required Probability and Statistics Median of 50% improvement in the median time to response, a statistical test is performed. The test shows that the new drug has achieved a 60% improvement in the median time to response compared to the standard treatment, which is well above the Required Probability and Statistics Median of 50%.
Based on these results, the company concludes that the new drug is effective in treating the medical condition and submits the data to regulatory agencies for approval. The Required Probability and Statistics Median helped the company set a specific goal and evaluate the success of the new drug based on measurable outcomes, which can inform future research and development efforts.
White paper on Median
White Paper: Understanding Probability and Statistics Median
Introduction: Probability and Statistics Median is a statistical concept used to describe the central tendency of a set of data. The median is the value that separates the upper and lower halves of a data set, and it is often used as a measure of central tendency when the data is skewed or contains outliers. In this white paper, we will explore the concept of Probability and Statistics Median, its calculation, and its applications in various fields.
What is Probability and Statistics Median? In statistics, the median is the middle value of a dataset, such that half of the values are above it and half are below it. It is a measure of central tendency that is less affected by extreme values or outliers than the mean. The median is often used to describe the typical value of a dataset when the data is skewed or contains outliers.
Calculating Probability and Statistics Median: To calculate the median of a dataset, the data is first arranged in order from smallest to largest. If there is an odd number of data points, the median is the middle value. If there is an even number of data points, the median is the average of the two middle values.
For example, consider the following dataset: 3, 7, 1, 9, 2. The data arranged in order from smallest to largest is: 1, 2, 3, 7, 9. The median is the middle value, which is 3.
Applications of Probability and Statistics Median: Probability and Statistics Median is widely used in various fields, including science, medicine, finance, marketing, and engineering. It is often used to describe the typical value of a dataset and to compare different datasets.
In science and medicine, the median is often used to describe the typical value of a set of measurements, such as the median survival time of patients with a specific medical condition.
In finance, the median return on investment is often used as a measure of central tendency to compare the performance of different investments.
In marketing, the median sales revenue is often used to describe the typical revenue generated by a product or service.
In engineering, the median failure time of a component is often used to estimate its reliability and to design systems that meet certain reliability criteria.
Conclusion: Probability and Statistics Median is a valuable statistical concept used to describe the central tendency of a dataset. It is less affected by extreme values or outliers than the mean, making it a useful measure of central tendency when the data is skewed or contains outliers. The median is widely used in various fields, including science, medicine, finance, marketing, and engineering, to describe the typical value of a dataset and to compare different datasets.