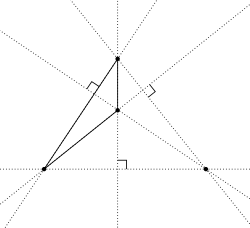
In calculation, an orthocentric framework is a bunch of four focuses on a plane, one of which is the orthocenter of the triangle shaped by the other three. Proportionately, the lines going through disjoint matches among the focuses are opposite, and the four circles going through any three of the four focuses have a similar range.

On the off chance that four focuses structure an orthocentric framework, every one of the four focuses is the orthocenter of the other three. These four potential triangles will all have a similar nine-point circle. Subsequently these four potential triangles should all have circumcircles with the equivalent circumradius.

Finding the Orthocenter

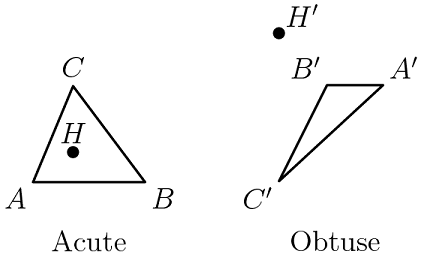
The area of the orthocenter relies upon the sort of triangle. Assuming the triangle is intense, the orthocenter will exist in it. Assuming the triangle is unfeeling, the orthocenter will lie beyond it. At long last, on the off chance that the triangle is correct, the orthocenter will be the vertex at the right point.

Since the three heights generally meet at a solitary point (evidence in a later segment), the orthocenter can be found by deciding the convergence of any two of them. This is particularly valuable while utilizing coordinate math since the estimations are emphatically improved on by the need to track down just two conditions of lines (and their crossing point).

Orthocenter of a Triangle

The orthocenter of a triangle is the point where the perpendicular drawn from the vertices to the opposite sides of the triangle intersect each other.

• For an acute angle triangle, the orthocenter lies inside the triangle.
• For the obtuse angle triangle, the orthocenter lies outside the triangle.
• For a right triangle, the orthocenter lies on the vertex of the right angle.

Take an example of a triangle ABC.

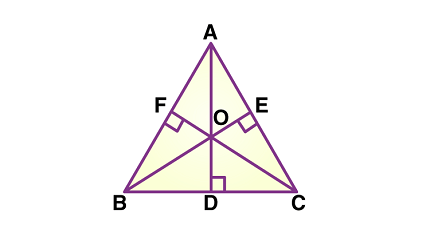
In the above figure, you can see, the perpendiculars AD, BE and CF drawn from vertex A, B and C to the opposite sides BC, AC and AB, respectively, intersect each other at a single point O. This point is the orthocenter of △ABC.

Orthocentric tetrahedron

In calculation, an orthocentric tetrahedron is a tetrahedron where every one of the three sets of inverse edges are opposite. It is otherwise called a symmetrical tetrahedron since symmetrical means opposite. It was first concentrated by Simon Lhuilier in 1782, and got the name orthocentric tetrahedron by G. de Longchamps in 1890.

In an orthocentric tetrahedron the four elevations are simultaneous. This normal point is known as the orthocenter, and it has the property that it is the symmetric place of the focal point of the encompassed circle regarding the centroid. Consequently the orthocenter concurs with the Monge point of the tetrahedron.

Finding the Orthocenter by Graphing

For the following examples, plot the three points, A, B, and C, on the Cartesian plane (an x-y grid) and connect the points with straight lines to form a triangle. Then, do the following:

• Predict where the orthocenter will be – inside the triangle, outside the triangle, or on the triangle. Support your prediction.
• Find the slopes of the sides AB, AC, and BC of the triangle. Use the slopes to draw the three altitudes of the triangle as shown in the lesson.
• Find the point of intersection of the altitudes – the orthocenter. Was your initial prediction correct?

Case Study on Orthocentre

Sure, here’s a brief case study on Orthocentre:

The orthocentre is a point where the three altitudes of a triangle intersect. In other words, it is the point where the perpendiculars drawn from the three vertices of a triangle to the opposite sides meet. The orthocentre has several interesting properties, including its location relative to the sides of the triangle.

Let’s consider a triangle ABC, where A, B, and C are the vertices. The altitudes from vertices A, B, and C are represented by AD, BE, and CF, respectively. These altitudes intersect at a point H, which is the orthocentre of the triangle.

One of the interesting properties of the orthocentre is that it is not necessarily located inside the triangle. In fact, the orthocentre is located inside the triangle only if the triangle is acute-angled. If the triangle is right-angled, the orthocentre coincides with the vertex opposite the hypotenuse. If the triangle is obtuse-angled, the orthocentre is located outside the triangle.

Another interesting property of the orthocentre is that it is the centre of the circumcircle of the triangle formed by the feet of the altitudes. In other words, if we draw the perpendiculars from the orthocentre to the three sides of the triangle, we obtain three new points: P, Q, and R. These points lie on a circle called the nine-point circle. This circle passes through the midpoints of the sides of the triangle, the feet of the altitudes, and the midpoint of the line segment joining the orthocentre to the circumcentre of the triangle.

The orthocentre also has applications in various fields, such as architecture, engineering, and physics. For example, in architecture, the orthocentre can be used to determine the point where the three walls of a room intersect. In engineering, the orthocentre can be used to calculate the stress on a beam that is supported by three points. In physics, the orthocentre can be used to calculate the moment of inertia of a three-dimensional object.

Conclusion

In conclusion, the orthocenter is an important point in analytical geometry that is associated with a triangle. It is the point where the altitudes of the triangle intersect, and its coordinates can be found using various methods, such as solving a system of equations or using vector calculus.

The properties of the orthocenter include the fact that it is the center of the triangle’s nine-point circle and that it lies on the Euler line, which connects the triangle’s centroid, circumcenter, and orthocenter. The orthocenter also has important geometric applications, such as determining the height of a mountain from two different viewpoints or finding the intersection point of three perpendicular lines.

Overall, the orthocenter is a fundamental concept in analytical geometry and plays an important role in many geometric problems and applications.

White paper on Orthocenter

Introduction

Analytical geometry is a branch of mathematics that uses algebraic methods to study geometric shapes and their properties. In this paper, we will focus on one of the key concepts in analytical geometry, the orthocenter of a triangle. The orthocenter is the point of intersection of the three altitudes of a triangle, and it has important applications in geometry and other fields.

Definition of the Orthocenter

The orthocenter of a triangle is defined as the point of intersection of the three altitudes of the triangle. An altitude is a line segment that connects a vertex of the triangle to the opposite side and is perpendicular to that side. The orthocenter is not always located inside the triangle; it can be inside, outside, or on the triangle itself.

Finding the Orthocenter To find the coordinates of the orthocenter, we can use several methods. One way is to use the slope-intercept form of the equations of the three altitudes and solve the resulting system of equations simultaneously. Another method is to use vector calculus and find the intersection point of the three lines formed by the vectors from the vertices to the opposite sides.

Properties of the Orthocenter

The orthocenter has several important properties. It is the center of the triangle’s nine-point circle, which passes through the midpoints of the sides, the feet of the altitudes, and the midpoint of the line segment connecting the orthocenter and the circumcenter. The nine-point circle is also tangent to the incircle and the three excircles of the triangle.

Conclusion

In conclusion, the orthocenter is an important concept in analytical geometry. It is the point where the altitudes of a triangle intersect, and it has several useful properties.

One important property is that the orthocenter is the center of the nine-point circle of a triangle. This circle passes through the midpoints of the sides, the feet of the altitudes, and the midpoint of the line segment connecting the orthocenter and the circumcenter.

Another property of the orthocenter is that it is the intersection of the perpendicular bisectors of the sides of the triangle. This means that the orthocenter is equidistant from the three vertices of the triangle.

Analytically, we can find the coordinates of the orthocenter by solving the system of equations formed by the equations of the altitudes. We can also use vectors to find the position vector of the orthocenter.

In summary, the orthocenter is an important point in analytical geometry that has several useful properties and can be found analytically using various methods.