Significant figures, also known as significant digits, are the digits in a number that are considered to be meaningful and relevant. They are used to indicate the precision of a measurement or calculation, and they help to ensure that results are reported with the appropriate level of accuracy.
The number of significant figures in a number is determined by the number of digits that are known with certainty, plus one digit that is uncertain or estimated. For example, the number 5.6 has two significant figures, because both the 5 and the 6 are known with certainty. The number 5.67 has three significant figures, because the 5 and the 6 are known with certainty, and the 7 is uncertain or estimated.
When performing calculations with numbers that have different numbers of significant figures, the final answer should be reported with the same number of significant figures as the least precise number used in the calculation. This is because the least precise number sets the limit on the precision of the final answer.
It’s important to pay attention to significant figures when performing calculations and reporting results, as failing to do so can lead to inaccuracies and errors.
What is Required General Significant Figures
The general rule for significant figures is to include all digits that are known with certainty, plus one digit that is uncertain or estimated. Here are the specific guidelines for determining significant figures:
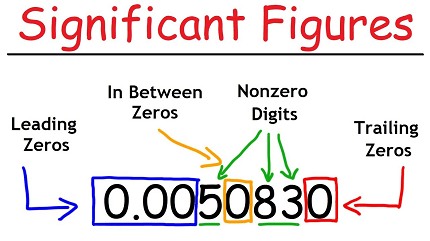
- Non-zero digits are always significant. For example, the number 145 has three significant figures.
- Zeros between non-zero digits are always significant. For example, the number 1005 has four significant figures.
- Leading zeros (zeros to the left of the first non-zero digit) are not significant. For example, the number 0.005 has one significant figure.
- Trailing zeros (zeros to the right of the last non-zero digit) are significant only if the number contains a decimal point. For example, the number 1.00 has three significant figures, but the number 1000 only has one significant figure.
- Exact numbers (numbers that are counted or defined) have an infinite number of significant figures. For example, there are exactly 12 eggs in a dozen, so the number 12 has an infinite number of significant figures.
When performing calculations with numbers that have different numbers of significant figures, the final answer should be rounded to the same number of significant figures as the least precise number used in the calculation. This ensures that the final answer is reported with the appropriate level of accuracy.
When is Required General Significant Figures
Significant figures are required in any situation where measurements or calculations are being made. They are important in science, engineering, and other fields where precise measurements and accurate calculations are necessary.
For example, significant figures are used when measuring the length of an object, the volume of a substance, or the time it takes for a reaction to occur. They are also used when performing calculations involving addition, subtraction, multiplication, and division, as well as more complex mathematical operations.
Significant figures help to ensure that measurements and calculations are reported with the appropriate level of precision, and they are essential for communicating scientific results accurately and effectively.
In summary, significant figures are required whenever measurements or calculations are being made, especially in scientific, engineering, and mathematical fields.
Where is Required General Significant Figures
Significant figures are used in many different fields and applications where measurements and calculations are made, including:
- Science: Significant figures are essential in science for accurately reporting measurements and calculations in fields such as physics, chemistry, and biology.
- Engineering: Significant figures are important in engineering for precise calculations and measurements in fields such as civil engineering, mechanical engineering, and electrical engineering.
- Mathematics: Significant figures are used in mathematics to ensure that calculations are performed with the appropriate level of precision.
- Finance: Significant figures are often used in finance for financial calculations such as interest rates, investment returns, and stock prices.
- Manufacturing: Significant figures are important in manufacturing for precise measurements and calculations in the production of products and materials.
- Quality control: Significant figures are used in quality control to ensure that measurements and calculations are accurate and reliable.
In summary, significant figures are used in many different fields and applications wherever precise measurements and calculations are required.
How is Required General Significant Figures
The process for determining the required number of significant figures involves the following steps:
- Identify the digits that are known with certainty: These are the digits that are read directly from the measuring instrument or are provided by a source that is known to be accurate.
- Identify the uncertain digit: The uncertain digit is the last digit that is estimated or interpolated. This digit should be rounded off to reflect the level of uncertainty in the measurement or calculation.
- Apply the rules for significant figures: Use the guidelines I mentioned earlier to determine the number of significant figures in the measurement or calculation.
- Apply the rules for rounding: Use the number of significant figures to determine how the uncertain digit should be rounded off.
For example, let’s say you are measuring the length of a pencil and the ruler you are using has marks at every millimeter. You measure the length of the pencil to be 15.4 mm. In this case, the digits 1, 5, and 4 are known with certainty, and the digit 4 is uncertain. Applying the rules for significant figures, we see that the number has three significant figures. To round off the uncertain digit, we look at the next digit to the right, which is a 0. Since this digit is less than 5, we round the 4 down to 0, giving a final result of 15.0 mm with three significant figures.
In summary, determining the required number of significant figures involves identifying the digits that are known with certainty, identifying the uncertain digit, applying the rules for significant figures, and then rounding off the uncertain digit according to those rules.
Nomenclature of General Significant Figures
The nomenclature of significant figures refers to the way in which significant figures are expressed in numerical notation. Here are some common terms used in nomenclature:
- Significant digits: Another term for significant figures, which are the digits that are known with certainty plus one digit that is uncertain or estimated.
- Leading zeros: Zeros that appear to the left of the first non-zero digit in a number, which are not significant.
- Trailing zeros: Zeros that appear to the right of the last non-zero digit in a number, which may or may not be significant depending on whether there is a decimal point present.
- Decimal places: The number of digits to the right of the decimal point in a number, which also determines the number of significant figures.
- Rounding: The process of adjusting a number to reflect the appropriate number of significant figures.
For example, if we have a number 1.2345 with five decimal places, but we only need to report it with three significant figures, we would round the number to 1.23. This would result in a number with two decimal places, but still only three significant figures.
In summary, the nomenclature of significant figures refers to the terms and concepts used to describe the way in which significant figures are expressed in numerical notation, including terms such as significant digits, leading and trailing zeros, decimal places, and rounding.
Case Study on General Significant Figures
Let’s consider a case study to see how significant figures are applied in practice.
Case Study: Measuring the Weight of a Substance
Suppose a chemist is trying to determine the weight of a substance using an electronic balance that measures to the nearest 0.01 grams. The chemist places the substance on the balance and records the measurement as 5.431 grams.
To determine the number of significant figures, we need to identify the digits that are known with certainty and the digit that is uncertain. In this case, the digits 5, 4, and 3 are known with certainty, and the digit 1 is uncertain. Therefore, the weight of the substance has four significant figures.
Next, let’s consider how to round the uncertain digit. The rule for rounding is that if the next digit to the right is less than 5, we round down, and if the next digit is 5 or greater, we round up. In this case, the next digit to the right is 0, which is less than 5. Therefore, we round the digit 1 down to 0. The weight of the substance, rounded to four significant figures, is 5.430 grams.
Suppose the chemist needs to perform a calculation using the weight of the substance. For example, suppose the chemist needs to calculate the density of the substance using the formula:
Density = mass/volume
If the volume of the substance is 10.00 mL, we can calculate the density as follows:
Density = 5.430 g/10.00 mL = 0.543 g/mL
To determine the number of significant figures in the density, we need to use the rule for significant figures in division, which is to use the smallest number of significant figures in the numerator or denominator. In this case, the weight of the substance has four significant figures, and the volume has four decimal places, but only two significant figures. Therefore, the density should be reported with two significant figures, which gives a final result of 0.54 g/mL.
In summary, this case study demonstrates how significant figures are used to report measurements with appropriate precision and how the rules for rounding and significant figures are applied in calculations. It also shows how the number of significant figures can affect the accuracy of calculations and the precision of the final result.
White paper on General Significant Figures
Introduction
Significant figures, also known as significant digits, are a way of expressing the accuracy and precision of measurements and calculations. In this white paper, we will discuss the concept of significant figures, their importance in scientific and technical fields, and the rules for using and reporting significant figures.
What are Significant Figures?
Significant figures are the digits in a number that are known with certainty, plus one digit that is uncertain or estimated. For example, if we measure the length of a table as 1.234 meters, the digits 1, 2, 3, and 4 are known with certainty, and the digit 4 is uncertain. Therefore, the length of the table has four significant figures.
Significant figures are used to express the precision of a measurement. A measurement with more significant figures is more precise than a measurement with fewer significant figures. For example, a measurement of 1.234 meters is more precise than a measurement of 1.2 meters because it has more significant figures.
Rules for Using Significant Figures
There are several rules for using significant figures:
- Non-zero digits are always significant. For example, the number 123 has three significant figures.
- Leading zeros are not significant. For example, the number 0.000123 has three significant figures.
- Trailing zeros are significant if there is a decimal point. For example, the number 123.00 has five significant figures.
- Trailing zeros are not significant if there is no decimal point. For example, the number 12300 has three significant figures.
- In calculations involving multiplication or division, the result should have the same number of significant figures as the number with the fewest significant figures. For example, if we multiply 1.23 by 4.567, the result should be reported as 5.62 because 1.23 has only two significant figures.
- In calculations involving addition or subtraction, the result should be rounded to the same decimal place as the number with the fewest decimal places. For example, if we add 1.23 and 4.567, the result should be reported as 5.80 because 1.23 has only two decimal places.
- In scientific notation, all digits are significant. For example, the number 1.23 x 10^4 has three significant figures.
Importance of Significant Figures
Significant figures are important in scientific and technical fields because they ensure that measurements and calculations are reported with appropriate precision. Using the correct number of significant figures can affect the accuracy of calculations and the validity of scientific conclusions. In addition, significant figures help to reduce measurement error by ensuring that the measurement is reported with appropriate precision.
Conclusion
Significant figures are a crucial concept in scientific and technical fields, and they are used to express the precision of measurements and calculations. By following the rules for using significant figures, scientists and technicians can ensure that their results are reported with appropriate precision and accuracy.
