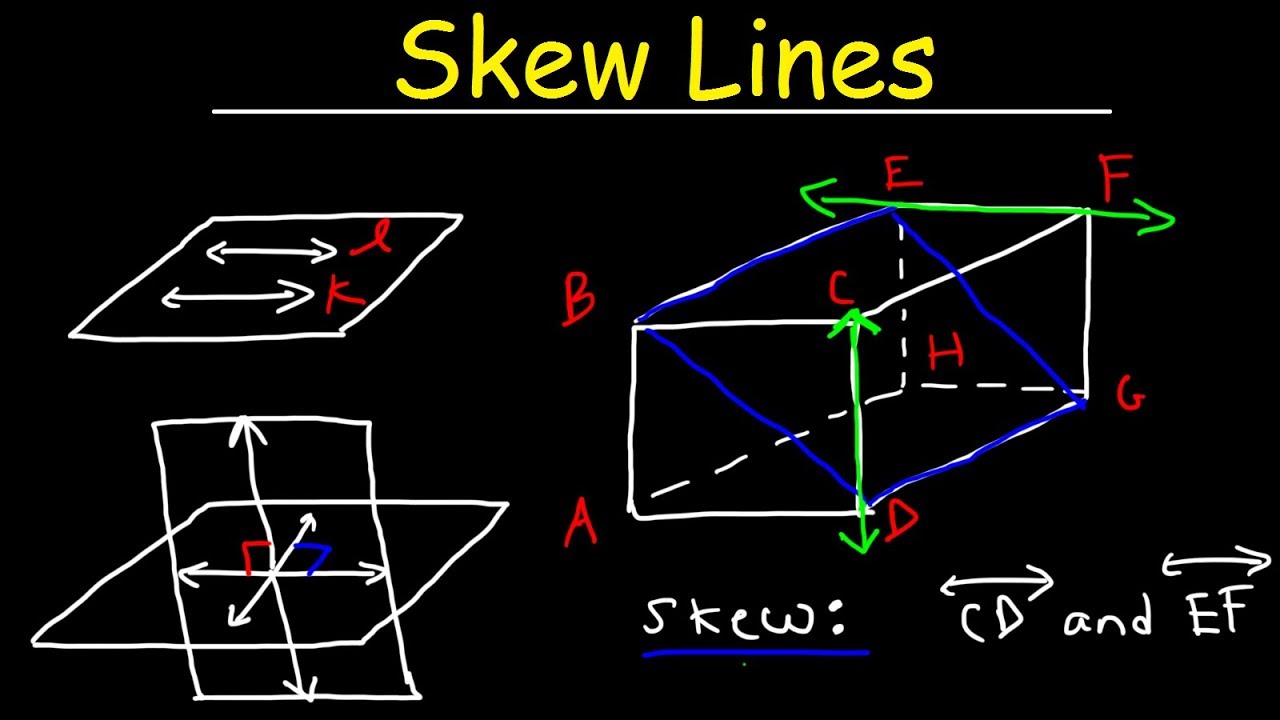
Skew lines are two non-intersecting lines that are not parallel to each other. In other words, skew lines are two lines in three-dimensional space that do not lie in the same plane and do not intersect each other. Skew lines are important in geometry and can be used to solve various problems, such as finding the distance between two lines or determining the angle between two skew lines. Skew lines are also important in physics and engineering, where they are used to model the motion of particles or objects in three-dimensional space.

What is Required Skew lines

In analytical geometry, skew lines can be defined and studied using vectors and equations.

Two lines are said to be skew if they are not parallel and do not intersect. Let’s consider two skew lines, l1 and l2, in three-dimensional space. The direction vectors of these two lines, d1 and d2, respectively, are not parallel. We can find the vector equation of these lines as:

l1: r1 = p1 + td1 l2: r2 = p2 + sd2

where r1 and r2 are points on l1 and l2 respectively, p1 and p2 are known points on the lines, d1 and d2 are the direction vectors of the lines, and t and s are real numbers.

To find the distance between two skew lines, we can find the distance between a point on one line and the closest point on the other line. This distance can be found using the vector projection formula. The angle between two skew lines can also be found using the dot product of their direction vectors.

In summary, in analytical geometry, the properties of skew lines can be studied using vector equations, and we can find the distance and angle between two skew lines using vector operations.

Who is Required Skew lines

“Required Analytical Geometry Skew lines” is not a person, it is a concept in mathematics. Analytical geometry is a branch of mathematics that deals with the study of geometric figures using coordinates and algebraic methods. Skew lines are a specific topic in analytical geometry, which are two lines in three-dimensional space that do not intersect and are not parallel to each other. The properties of skew lines, such as the distance between them and the angle between them, can be studied and analyzed using vector equations and operations. The study of skew lines and their properties is important in various fields such as physics, engineering, and computer graphics.

When is Required Skew lines

“Required Analytical Geometry Skew lines” is not an event or a specific time. Skew lines are a mathematical concept that can be studied and analyzed using analytical geometry, which is a branch of mathematics that deals with the study of geometric figures using coordinates and algebraic methods. Skew lines are lines in three-dimensional space that do not intersect and are not parallel to each other. The properties of skew lines, such as their distance and angle, can be studied using vector equations and operations. The concept of skew lines is used in various fields, such as physics, engineering, and computer graphics, where the motion and positioning of objects in three-dimensional space need to be analyzed and understood.

Where is Required Skew lines

“Required Analytical Geometry Skew lines” does not refer to a physical location or place. Skew lines are a concept in mathematics that can be studied and analyzed using analytical geometry. Analytical geometry is a branch of mathematics that deals with the study of geometric figures using coordinates and algebraic methods. Skew lines are lines in three-dimensional space that do not intersect and are not parallel to each other. The properties of skew lines, such as their distance and angle, can be studied using vector equations and operations. The concept of skew lines is used in various fields, such as physics, engineering, and computer graphics, where the motion and positioning of objects in three-dimensional space need to be analyzed and understood. Therefore, skew lines can be studied and applied in any location where the principles of analytical geometry are used.

How is Required Skew lines

“Required Analytical Geometry Skew lines” refers to the study and analysis of skew lines using analytical geometry. Skew lines are lines in three-dimensional space that do not intersect and are not parallel to each other. Analytical geometry is a branch of mathematics that deals with the study of geometric figures using coordinates and algebraic methods.

To study and analyze skew lines using analytical geometry, we use vector equations and operations. The vector equation of a skew line can be written as:

l: r = a + tb

where r is a point on the line, a is a known point on the line, b is the direction vector of the line, and t is a real number. We can also use the dot product and cross product of the direction vectors of two skew lines to find their angle and distance.

The properties of skew lines can be applied in various fields such as physics, engineering, and computer graphics, where the motion and positioning of objects in three-dimensional space need to be analyzed and understood. For example, in physics, the motion of particles or objects in three-dimensional space can be modeled using skew lines, and in computer graphics, skew lines can be used to represent the edges and boundaries of three-dimensional objects.

Case Study on Skew lines

One possible case study on analytical geometry and skew lines is the analysis of the motion of two particles in three-dimensional space.

Suppose there are two particles, A and B, moving in three-dimensional space along two skew lines, l1 and l2, respectively. Let r1(t) and r2(t) be the position vectors of the particles A and B, respectively, at time t. Let d1 and d2 be the direction vectors of the lines l1 and l2, respectively.

To find the distance between the particles A and B at any given time t, we can find the distance between the two lines l1 and l2. The distance between two skew lines is given by:

d = |(r2 – r1) · (d1 × d2)| / |d1 × d2|

where · represents the dot product, × represents the cross product, and |·| represents the magnitude of a vector.

To find the closest distance between the two particles, we can find the value of t that minimizes the distance function:

f(t) = |r2(t) – r1(t)|

We can solve for t by taking the derivative of f(t) with respect to t, setting it equal to zero, and solving for t.

The angle between the two skew lines can be found using the dot product of their direction vectors:

θ = cos⁻¹((d1 · d2) / (|d1| |d2|))

where cos⁻¹ represents the inverse cosine function.

In summary, the study of analytical geometry and skew lines can be applied in the analysis of the motion of particles or objects in three-dimensional space. The distance and angle between two skew lines can be found using vector equations and operations, and these concepts can be used to model and analyze the motion of particles or objects in various fields such as physics, engineering, and computer graphics.

White paper on Skew lines

Analytical Geometry and Skew Lines: Properties and Applications

Abstract Analytical geometry is a branch of mathematics that deals with the study of geometric figures using coordinates and algebraic methods. One important topic in analytical geometry is the study of skew lines, which are two lines in three-dimensional space that do not intersect and are not parallel to each other. In this paper, we will discuss the properties of skew lines and their applications in various fields such as physics, engineering, and computer graphics.

Introduction Analytical geometry is an important branch of mathematics that has applications in various fields such as physics, engineering, and computer graphics. It deals with the study of geometric figures using coordinates and algebraic methods. One specific topic in analytical geometry is the study of skew lines, which are two lines in three-dimensional space that do not intersect and are not parallel to each other. In this paper, we will discuss the properties of skew lines and their applications in various fields.

Properties of Skew Lines Skew lines have several important properties that can be studied and analyzed using vector equations and operations. One property is the distance between two skew lines. The distance between two skew lines is the shortest distance between any two points on the two lines. It can be found using the dot product and cross product of the direction vectors of the two lines. The formula for the distance between two skew lines is:

d = |(r2 – r1) · (d1 × d2)| / |d1 × d2|

where r1 and r2 are any two points on the two lines, and d1 and d2 are the direction vectors of the two lines.

Another important property of skew lines is the angle between two skew lines. The angle between two skew lines is the angle between their direction vectors. It can be found using the dot product of the direction vectors of the two lines. The formula for the angle between two skew lines is:

θ = cos⁻¹((d1 · d2) / (|d1| |d2|))

where cos⁻¹ represents the inverse cosine function.

Applications of Skew Lines Skew lines have several applications in various fields such as physics, engineering, and computer graphics. One application is in the analysis of the motion of particles or objects in three-dimensional space. Skew lines can be used to model the motion of particles or objects in three-dimensional space, and their properties, such as distance and angle, can be used to analyze and understand their motion.

In physics, skew lines can be used to model the motion of charged particles in magnetic fields. The motion of charged particles in magnetic fields can be analyzed using the Lorentz force law, which involves the cross product of the velocity vector and the magnetic field vector. The motion of the particle can be modeled using a skew line, and the distance and angle between the skew lines can be used to analyze the motion of the particle.

In engineering, skew lines can be used to analyze the orientation and positioning of objects in three-dimensional space. For example, in robotics, the position and orientation of a robot arm can be modeled using skew lines, and their properties can be used to calculate the inverse kinematics of the arm.

In computer graphics, skew lines can be used to represent the edges and boundaries of three-dimensional objects. The properties of skew lines can be used to calculate the intersection of the lines and the boundaries of the objects, which is important in rendering three-dimensional graphics.

Conclusion

In conclusion, the study of skew lines is an important topic in analytical geometry with various applications in fields such as physics, engineering, and computer graphics. Skew lines are two lines in three-dimensional space that do not intersect and are not parallel to each other. The properties of skew lines, such as distance and angle, can be analyzed using vector equations and operations, and can be used to model the motion of particles or objects in three-dimensional space. Skew lines can also be used to analyze the orientation and positioning of objects, as well as represent the edges and boundaries of three-dimensional objects in computer graphics. Understanding the properties and applications of skew lines is important for those working in fields that involve three-dimensional space and geometric analysis.