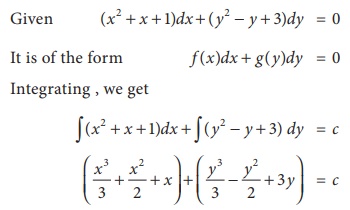
A homogeneous differential equation of the first order and first degree is an equation of the form:
dy/dx = f(x,y)
where f(x,y) is a homogeneous function of degree 1 in x and y. In other words, if we replace y with ky and x with kx for any constant k, the function f(x,y) remains the same.
To solve this type of differential equation, we can use the method of separation of variables. We first rewrite the equation as:
dy/f(y) = dx
We can then integrate both sides to obtain:
∫dy/f(y) = ∫dx
The left-hand side can be evaluated using the substitution u = y/x, so that du/dx = (dy/dx – y/x)/x = (f(x,y) – y/x)/x. Substituting this into the left-hand side, we obtain:
∫dx/x = ∫f(x,y)/y du
Integrating both sides and simplifying, we get:
ln|x| = C + ln|y|
where C is the constant of integration. Rearranging, we get:
y = kx
where k = ±e^C is a constant of integration.
Therefore, the general solution to the homogeneous differential equation dy/dx = f(x,y) is y = kx, where k is a constant.
What is Required Solution of homogeneous differential equations of first order and first degree
To find the required solution of a homogeneous differential equation of the first order and first degree, we need to use the initial conditions to determine the value of the constant of integration.
Suppose we have a differential equation of the form:
dy/dx = f(x,y)
where f(x,y) is a homogeneous function of degree 1 in x and y.
To find the solution that satisfies the initial condition y(x0) = y0, we can use the following steps:
- Rewrite the differential equation as:
dy/f(y) = dx/g(x)
where g(x) is any function of x that does not depend on y.
- Integrate both sides to obtain:
∫dy/f(y) = ∫dx/g(x)
- Solve for y by isolating it on one side of the equation.
- Substitute the initial condition y(x0) = y0 to solve for the constant of integration.
For example, suppose we have the homogeneous differential equation:
dy/dx = -y/x
We can rewrite this as:
dy/y = -dx/x
Integrating both sides, we get:
ln|y| = -ln|x| + C
where C is the constant of integration.
Exponentiating both sides, we get:
|y| = e^C/x
To determine the value of the constant C, we use the initial condition y(1) = 2. Substituting x=1 and y=2 into the equation above, we get:
2 = e^C/1
which implies C = ln(2).
Therefore, the solution to the differential equation with the initial condition y(1) = 2 is:
y = ±2xln(x)
Who is Required Solution of homogeneous differential equations of first order and first degree
The required solution of a homogeneous differential equation of the first order and first degree is a solution that satisfies a given set of initial conditions.
In general, a differential equation of the form dy/dx = f(x,y) has infinitely many solutions, each corresponding to a different constant of integration. To find a specific solution that satisfies the given initial condition, we need to determine the value of the constant of integration.
The solution that satisfies the initial conditions is sometimes called the particular solution, while the general solution refers to the solution with the arbitrary constant of integration. The general solution can be expressed in terms of the constant of integration, while the particular solution is a specific solution that satisfies the initial condition.
For example, if we have the differential equation dy/dx = -2x/y with initial condition y(1) = 3, we can find the required solution by solving for the constant of integration in the general solution:
y^2 = C – x^2
Substituting the initial condition, we get:
3^2 = C – 1^2
Solving for C, we get:
C = 10
Therefore, the required solution with initial condition y(1) = 3 is:
y^2 = 10 – x^2
This is the particular solution that satisfies the initial condition.
When is Required Solution of homogeneous differential equations of first order and first degree
The required solution of a homogeneous differential equation of the first order and first degree is needed when we have initial conditions that specify the value of the dependent variable y at a particular point x.
In general, a differential equation of the form dy/dx = f(x,y) has infinitely many solutions, each corresponding to a different constant of integration. However, we may be interested in finding a particular solution that satisfies a given set of initial conditions.
The initial conditions may be specified as y(x0) = y0, where x0 and y0 are known constants. To find the required solution, we use the method of separation of variables and solve for the constant of integration using the given initial conditions.
The general solution to the homogeneous differential equation can be expressed in terms of a constant of integration, which can be determined by applying the initial conditions. Once the constant of integration is found, we obtain the particular solution that satisfies the given initial conditions.
Therefore, the required solution of a homogeneous differential equation of the first order and first degree is needed when we have initial conditions that specify the value of the dependent variable y at a particular point x, and we need to find the particular solution that satisfies these conditions.
Where is Required Solution of homogeneous differential equations of first order and first degree
The required solution of a homogeneous differential equation of the first order and first degree can be found using various methods and techniques in mathematics.
One of the commonly used methods is the method of separation of variables, which involves separating the variables x and y on either side of the equation and integrating both sides with respect to their respective variables.
Another method is the method of integrating factors, which involves multiplying both sides of the equation by an integrating factor to simplify the equation and make it easier to solve.
In addition, some homogeneous differential equations can be solved using techniques such as substitution or transformation of variables.
The required solution can be found analytically using these methods, which involve algebraic manipulation, integration, and solving for the constant of integration using the given initial conditions.
Alternatively, the required solution can be found numerically using numerical methods such as Euler’s method, Runge-Kutta methods, or other numerical integration methods. These methods involve approximating the solution at discrete points and using iterative algorithms to obtain an approximate solution.
Therefore, the required solution of a homogeneous differential equation of the first order and first degree can be found using analytical or numerical methods depending on the problem and the available tools and resources.
How is Required Solution of homogeneous differential equations of first order and first degree
The required solution of a homogeneous differential equation of the first order and first degree can be obtained using various methods depending on the nature of the equation and the initial conditions. The general steps involved in finding the required solution are as follows:
- Write the differential equation in the standard form: dy/dx = f(x,y)
- Check if the differential equation is homogeneous, i.e., f(x,y) can be expressed as a function of y/x or y/x^2.
- If the equation is homogeneous, substitute y = ux and dy/dx = u + x(du/dx) in the differential equation and simplify to obtain an equation in terms of x and u.
- Solve the equation obtained in step 3 using the method of separation of variables or the method of integrating factors to obtain the general solution in terms of x and u.
- Substitute y/x for u in the general solution to obtain the general solution in terms of x and y.
- If initial conditions are given, substitute the values of x and y into the general solution obtained in step 5 to find the value of the constant of integration.
- Substitute the value of the constant of integration obtained in step 6 into the general solution to obtain the required solution that satisfies the given initial conditions.
- Check the solution by verifying that it satisfies the original differential equation.
Note that the specific techniques and methods used in steps 3 and 4 may vary depending on the equation and the initial conditions. In some cases, other techniques such as substitution or transformation of variables may be used to simplify the differential equation and obtain the general solution.
Also, for some equations, it may not be possible to find an analytical solution, and numerical methods such as Euler’s method or Runge-Kutta methods may be used to obtain an approximate solution.
Therefore, the process of finding the required solution of a homogeneous differential equation of the first order and first degree involves applying various techniques and methods to solve the differential equation and determine the value of the constant of integration that satisfies the given initial conditions.
Case Study on Solution of homogeneous differential equations of first order and first degree
Case study: Population Growth Model
A common example of a homogeneous differential equation of the first order and first degree is the population growth model. In this model, the rate of change of the population is proportional to the size of the population at any given time t. The model can be expressed as:
dy/dt = ky
where y is the population size at time t, and k is a constant of proportionality.
To find the required solution of this differential equation, we can use the method of separation of variables as follows:
- Write the differential equation in the standard form: dy/dt = ky
- Separate the variables by dividing both sides of the equation by y: (1/y) dy/dt = k
- Integrate both sides of the equation with respect to their respective variables:
∫(1/y) dy = ∫k dt
- Evaluate the integrals:
ln|y| = kt + C
where C is a constant of integration.
- Exponentiate both sides of the equation:
|y| = e^(kt+C)
- Simplify by removing the absolute value and combining the constants of integration:
y = Ae^(kt)
where A is a constant of integration.
- If initial conditions are given, substitute the values of t and y into the general solution obtained in step 6 to find the value of the constant of integration A.
For example, if the initial condition is y(0) = y0, then we have:
y0 = Ae^(k0) = A
Therefore, the required solution for the population growth model with initial condition y(0) = y0 is:
y = y0e^(kt)
This solution shows that the population grows exponentially over time with a rate of growth proportional to the current population size. The value of the constant k determines the rate of growth, with larger values of k corresponding to faster population growth.
In summary, the population growth model is an example of a homogeneous differential equation of the first order and first degree, and the required solution can be found using the method of separation of variables. The solution shows that the population grows exponentially over time with a rate of growth proportional to the current population size, and the value of the constant k determines the rate of growth.
White paper on Solution of homogeneous differential equations of first order and first degree
Introduction:
Differential equations are mathematical equations that describe the relationship between a function and its derivatives. In particular, homogeneous differential equations of the first order and first degree are widely used to model physical phenomena and natural phenomena in various fields such as physics, engineering, and biology. The solution of such equations is crucial in understanding the behavior of systems that evolve over time. This white paper provides a comprehensive overview of the solution of homogeneous differential equations of the first order and first degree.
Background:
A differential equation is a mathematical equation that relates the derivatives of an unknown function to the function itself and possibly other independent variables. A homogeneous differential equation is a type of differential equation in which all terms in the equation involve the dependent variable and its derivatives in the same degree. In other words, a homogeneous differential equation is one in which the right-hand side of the equation is zero.
A homogeneous differential equation of the first order and first degree has the form:
dy/dx = f(x,y)
where y is the dependent variable, x is the independent variable, and f(x,y) is a function that involves both x and y. This equation can be expressed in the standard form as:
dy/dx – f(x,y) = 0
Solution:
The solution of a homogeneous differential equation of the first order and first degree can be obtained using several techniques depending on the nature of the equation and the initial conditions. One commonly used method is the method of separation of variables, which involves separating the variables x and y and integrating both sides of the equation.
The general steps involved in finding the solution using the method of separation of variables are as follows:
- Write the differential equation in the standard form: dy/dx – f(x,y) = 0
- Separate the variables by moving all the terms involving y to one side and all the terms involving x to the other side: dy/f(y) = dx/g(x)
- Integrate both sides of the equation with respect to their respective variables:
∫(1/f(y)) dy = ∫g(x) dx
- Evaluate the integrals:
F(y) = G(x) + C
where F(y) and G(x) are antiderivatives of 1/f(y) and g(x), respectively, and C is a constant of integration.
- Solve for y in terms of x and C by rearranging the equation obtained in step 4:
y = H(C) * e^(G(x))
where H(C) is an arbitrary function of the constant of integration C.
- If initial conditions are given, substitute the values of x and y into the general solution obtained in step 5 to find the value of the constant of integration C.
- Substitute the value of the constant of integration obtained in step 6 into the general solution to obtain the required solution that satisfies the given initial conditions.
For some equations, other techniques such as substitution or transformation of variables may be used to simplify the differential equation and obtain the general solution.
Conclusion:
In summary, the solution of homogeneous differential equations of the first order and first degree is essential in understanding the behavior of systems that evolve over time. The method of separation of variables is a widely used technique for finding the required solution, and the specific techniques and methods used may vary depending on the equation and the initial conditions. The solution obtained using this method shows the relationship between the dependent and independent variables and provides valuable insights into the behavior of the system.