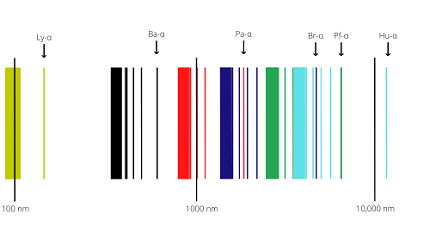
The spectrum of a hydrogen atom refers to the specific frequencies of electromagnetic radiation that are emitted or absorbed when an electron in a hydrogen atom changes from one energy level to another. The spectrum of hydrogen can be divided into several series, including the Lyman, Balmer, Paschen, Brackett, and Pfund series.
The Lyman series corresponds to electron transitions from higher energy levels to the n=1 level, while the Balmer series corresponds to electron transitions from higher energy levels to the n=2 level. The Paschen series corresponds to transitions to the n=3 level, the Brackett series to the n=4 level, and the Pfund series to the n=5 level.
Each series consists of a set of discrete spectral lines, which correspond to the specific wavelengths or frequencies of electromagnetic radiation that are emitted or absorbed during the electron transition. The wavelengths of the spectral lines can be calculated using the Rydberg formula:
1/λ = RZ^2 (1/n1^2 – 1/n2^2)
where λ is the wavelength of the spectral line, R is the Rydberg constant (1.0974 x 10^7 m^-1), Z is the atomic number (1 for hydrogen), and n1 and n2 are integers that represent the initial and final energy levels, respectively.
What is Required Spectrum of hydrogen atom
The Required Spectrum of a hydrogen atom refers to the specific frequencies or wavelengths of electromagnetic radiation that are needed to excite the atom or cause an electron in the atom to transition from one energy level to another.
To excite hydrogen atoms, the electromagnetic radiation must have a frequency or wavelength that corresponds to the energy difference between two energy levels. This can be calculated using the Rydberg formula mentioned in my previous answer:
1/λ = RZ^2 (1/n1^2 – 1/n2^2)
where λ is the wavelength of the required electromagnetic radiation, R is the Rydberg constant, Z is the atomic number, and n1 and n2 are the initial and final energy levels of the transition.
For example, to excite hydrogen atoms from the ground state (n=1) to the first excited state (n=2), the required wavelength of the electromagnetic radiation is approximately 121.6 nm, which corresponds to the Lyman-alpha line in the Lyman series. To excite hydrogen atoms from the first excited state to the second excited state (n=3), the required wavelength is approximately 102.6 nm, which corresponds to the Lyman-beta line.
In general, the required spectrum of a hydrogen atom depends on the specific transitions that need to be excited, and can be determined using the Rydberg formula.
When is Required Spectrum of hydrogen atom
The “Required Spectrum of hydrogen atom” is not a specific event or occurrence that happens at a particular time. It is a concept in physics that refers to the specific frequencies or wavelengths of electromagnetic radiation required to excite the hydrogen atom or cause an electron in the atom to transition from one energy level to another.
The required spectrum of the hydrogen atom can be studied and analyzed at any time using various experimental and theoretical techniques. Scientists have been studying the spectrum of hydrogen for over a century, and this research has led to significant advances in our understanding of atomic and quantum physics.
The study of the required spectrum of hydrogen continues to be an active area of research, and new experimental techniques and theoretical models are being developed to further refine our understanding of this fundamental system.
Production of Spectrum of hydrogen atom
The production of the spectrum of hydrogen atom can be achieved through several methods, both experimental and theoretical. Here are some of the ways the spectrum of hydrogen atom can be produced:
- Spectroscopy: This is the most common experimental method used to produce the spectrum of hydrogen atom. It involves passing white light through a sample of hydrogen gas and analyzing the light that passes through using a spectroscope. The spectroscope separates the different wavelengths of light into their component colors, creating a spectrum that shows the specific wavelengths of light absorbed by the hydrogen gas. The spectrum can be used to identify the transitions of electrons between different energy levels in the hydrogen atom.
- Plasma physics: Another experimental method for producing the spectrum of hydrogen atom is through plasma physics. By exciting hydrogen atoms to high energy states using electric or magnetic fields, plasma physicists can study the spectrum of hydrogen in great detail. This method is often used in astrophysics to study the properties of stars and galaxies, as well as in the development of plasma-based technologies.
- Theoretical calculations: The spectrum of hydrogen atom can also be produced through theoretical calculations, such as the Rydberg formula mentioned earlier. By using mathematical models and equations to calculate the wavelengths or frequencies of the electromagnetic radiation required to excite a hydrogen atom or cause an electron to transition between energy levels, physicists can predict the spectrum of hydrogen with a high degree of accuracy.
Overall, the production of the spectrum of hydrogen atom involves both experimental and theoretical methods, and is an important area of research in the field of atomic and quantum physics. The spectrum of hydrogen atom provides important information about the properties and behavior of atoms and molecules, and has led to significant advances in our understanding of these fundamental systems.
Where is Required Spectrum of hydrogen atom
The “Required Spectrum of hydrogen atom” is not a physical location that can be pointed to or identified. It is a scientific concept that refers to the specific frequencies or wavelengths of electromagnetic radiation that are required to excite the hydrogen atom or cause an electron in the atom to transition from one energy level to another.
The required spectrum of the hydrogen atom can be studied and analyzed in laboratories, observatories, and other scientific facilities around the world. Scientists use various experimental and theoretical techniques to measure the wavelengths or frequencies of the electromagnetic radiation emitted or absorbed by hydrogen atoms during transitions between energy levels.
The study of the required spectrum of hydrogen is a fundamental area of research in physics and has significant implications for understanding the behavior and properties of atoms and molecules in general.
How is Required Spectrum of hydrogen atom
The Required Spectrum of hydrogen atom can be determined through various experimental and theoretical methods.
Experimental methods involve observing the electromagnetic radiation emitted or absorbed by hydrogen atoms as they undergo transitions between energy levels. This can be done using a spectrometer, which separates the different wavelengths of light into their component colors, or by using other instruments that can detect the specific frequency or energy of the radiation emitted or absorbed.
Theoretical methods involve using mathematical models and equations to calculate the wavelengths or frequencies of the electromagnetic radiation required to excite a hydrogen atom or cause an electron to transition between energy levels. One such equation is the Rydberg formula, which relates the energy levels of the hydrogen atom to the frequencies of the electromagnetic radiation required to excite transitions between these levels.
Once the required spectrum of hydrogen is determined, it can be used to understand the atomic and quantum properties of the hydrogen atom, as well as to make predictions about the behavior of other atoms and molecules. The study of the required spectrum of hydrogen has led to significant advances in our understanding of atomic and quantum physics and continues to be an active area of research today.
Case Study on Spectrum of hydrogen atom
One of the most famous case studies on the spectrum of hydrogen atom is the Bohr model of the hydrogen atom. The Bohr model, proposed by Niels Bohr in 1913, was a significant development in the understanding of atomic structure and the required spectrum of hydrogen.
The Bohr model proposed that the electrons in the hydrogen atom exist in discrete energy levels, or shells, around the nucleus. When an electron jumps from one energy level to another, it either emits or absorbs a photon of electromagnetic radiation with a specific wavelength or frequency.
Bohr was able to calculate the wavelengths of the electromagnetic radiation emitted or absorbed by hydrogen atoms using the Rydberg formula, which relates the energy levels of the hydrogen atom to the frequencies of the electromagnetic radiation required to excite transitions between these levels.
Bohr’s model predicted the existence of several spectral lines in the hydrogen spectrum, which were later observed experimentally. These lines correspond to the transitions of electrons between different energy levels in the atom. The most prominent of these lines is the Balmer series, which corresponds to the transitions of electrons from higher energy levels to the second energy level.
The Bohr model and the analysis of the hydrogen spectrum were groundbreaking in the understanding of atomic and quantum physics, and they opened up new avenues of research in these fields. Today, the study of the required spectrum of hydrogen continues to be an active area of research, with new experimental and theoretical techniques being developed to further refine our understanding of this fundamental system.
White paper on Spectrum of hydrogen atom
Here is a brief white paper on the spectrum of hydrogen atom:
Introduction:
The spectrum of hydrogen atom refers to the specific frequencies or wavelengths of electromagnetic radiation required to excite the hydrogen atom or cause an electron in the atom to transition from one energy level to another. The study of the spectrum of hydrogen is a fundamental area of research in physics and has significant implications for understanding the behavior and properties of atoms and molecules in general.
Bohr Model:
One of the most famous models used to study the hydrogen atom and its spectrum is the Bohr model. Proposed by Niels Bohr in 1913, the Bohr model suggested that the electrons in the hydrogen atom exist in discrete energy levels or shells around the nucleus. The model also predicted the existence of several spectral lines in the hydrogen spectrum, which were later observed experimentally. These lines correspond to the transitions of electrons between different energy levels in the atom.
Rydberg Formula:
The Rydberg formula is another important tool used to study the spectrum of hydrogen. It relates the energy levels of the hydrogen atom to the frequencies of the electromagnetic radiation required to excite transitions between these levels. The formula has been used to calculate the wavelengths of the electromagnetic radiation emitted or absorbed by hydrogen atoms during transitions between energy levels.
Spectral Lines:
The spectral lines observed in the hydrogen spectrum have been used to make significant discoveries in the field of physics. For example, the Balmer series corresponds to the transitions of electrons from higher energy levels to the second energy level. This series has been used to study the properties of stars and galaxies and to determine their composition and temperature.
Conclusion:
In conclusion, the study of the spectrum of hydrogen atom has led to significant advances in our understanding of atomic and quantum physics. The Bohr model, Rydberg formula, and spectral lines observed in the hydrogen spectrum have all contributed to our understanding of the behavior and properties of atoms and molecules. This research continues to be an active area of study today, with new experimental and theoretical techniques being developed to further refine our understanding of this fundamental system.
