Square pyramidal – Vrindawan Coaching Center

A square pyramid is a type of three-dimensional geometric shape that consists of a square base and four triangular faces that meet at a common point called the apex or vertex. The base of the pyramid is a square, and the four triangular faces are equilateral triangles.

The formula for the volume of a square pyramid is given by: V = (B * h) / 3 where B is the area of the base (which is a square) and h is the height of the pyramid (the perpendicular distance from the base to the apex).

The formula for the surface area of a square pyramid is given by: A = B + 4 * (0.5 * l * s) where B is the area of the base (which is a square), l is the slant height of the pyramid (the distance from the apex to any corner of the base), and s is the length of the sides of the base (since it is a square, all sides are equal).

What is Required Square pyramidal

A square pyramidal is a type of pyramid with a square base and four triangular faces that meet at a common vertex. To define a square pyramid, the following requirements must be met:

Base: The pyramid must have a square base, which means all four sides of the base are equal in length and all four angles between the sides are right angles (90 degrees).
Triangular faces: The pyramid must have four triangular faces that connect the vertices of the base to the common vertex (apex). Each triangular face must have three sides and three angles, with the base forming one of the sides and the apex forming the common vertex of all four triangles.
Vertex: The four triangular faces must meet at a single point called the apex or vertex, which is the topmost point of the pyramid. The apex must be directly above the center of the base and form right angles with the sides of the base.
Symmetry: The pyramid must exhibit symmetry along its vertical axis, meaning that if it is divided into two halves along a vertical plane passing through the apex and the center of the base, the two halves must be mirror images of each other.

These are the basic requirements for a pyramid to be classified as a square pyramidal. Additional properties and characteristics may vary depending on the specific context or application. So, a square base, triangular faces, a common apex, and symmetry are the main requirements for a pyramid to be considered square pyramidal. Overall, the term “square pyramidal” refers to the geometric shape and structure of a pyramid with a square base. It is important to note that there may be different definitions or requirements for square pyramidal in different fields or contexts, such as in mathematics, geometry, architecture, or chemistry. It is always best to consult relevant sources or experts for specific requirements or definitions in a particular field or application.

When is Required Square pyramidal

In math, a square pyramid is a pyramid having a square base. On the off chance that the zenith is oppositely over the focal point of the square, it is a right square pyramid, and has C4v evenness. Assuming all edge lengths are equivalent, it is a symmetrical square pyramid, the Johnson strong J1.

General square pyramid

A perhaps sideways square pyramid with base length l and opposite level h has volume:

Right square pyramid

In a right square pyramid, every one of the sidelong edges have a similar length, and the sides other than the base are consistent isosceles triangles.

A right square pyramid with base length l and height h has surface area and volume:

$A=l^{2}+l{\sqrt {l^{2}+4h^{2}}}$ ,

$V={\frac {1}{3}}l^{2}h$ .

The lateral edge length is:

${\sqrt {h^{2}+{{l^{2}} \over {2}}}}$ ;

the slant height is:

${\sqrt {h^{2}+{{l^{2}} \over {4}}}}$ .

The dihedral angles are:

between the base and a side:

$\arctan \left({{2\,h} \over {l}}\right)$ ;

between two sides:

$\arccos \left({{-l^{2}} \over {l^{2}+4\,h^{2}}}\right)$ .

Square pyramidal number

In science, a pyramid number, or square pyramidal number, is a characteristic number that counts the quantity of stacked circles in a pyramid with a square base. The investigation of these numbers returns to Archimedes and Fibonacci. They are essential for a more extensive subject of figurate numbers addressing the quantities of focuses framing normal examples inside various shapes.

As well as including circles in a pyramid, these numbers can be depicted mathematically as an amount of the first
n positive square numbers, or as the upsides of a cubic polynomial. They can be utilized to tackle a few other counting issues, remembering counting squares for a square matrix and counting intense triangles framed from the vertices of an odd ordinary polygon. They equivalent the amounts of back to back tetrahedral numbers, and are one-fourth of a bigger tetrahedral number. The amount of two back to back square pyramidal numbers is an octahedral number.

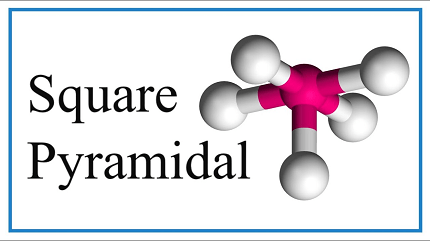
Square pyramidal molecular geometry

In sub-atomic calculation, square pyramidal math depicts the state of specific mixtures with the recipe ML5 where L is a ligand. Assuming the ligand particles were associated, the subsequent shape would be that of a pyramid with a square base. The point bunch evenness included is of type C4v. The math is normal for specific primary gathering intensifies that have a stereochemically-dynamic solitary pair, as portrayed by VSEPR hypothesis. Certain mixtures solidify in both the three-sided bipyramidal and the square pyramidal designs, remarkably [Ni(CN)5]3.

Elongated square pyramid

In calculation, the stretched square pyramid is one of the Johnson solids (J8). As the name proposes, it tends to be developed by prolonging a square pyramid (J1) by joining a 3D shape to its square base. Like any lengthened pyramid, it is topologically (yet not mathematically) self-double.

A Johnson strong is one of 92 stringently curved polyhedra that is made out of customary polygon faces however are not uniform polyhedra (that is, they are not Dispassionate solids, Archimedean solids, crystals, or antiprisms). They were named by Norman Johnson, who previously recorded these polyhedra in 1966.