Aggregate most normally implies the all out of at least two numbers added together; see option.

Aggregate can likewise allude to:

Mathematics

Aggregate (classification hypothesis), the conventional idea of summation in science
Total, the consequence of summation, the expansion of a succession of numbers
3SUM, a term from computational intricacy hypothesis
Band total, an approach to interfacing numerical bunches
Associated total, an approach to sticking manifolds
Digit aggregate, in number hypothesis
Direct total, a blend of logarithmic items
Direct amount of gatherings
Direct amount of modules
Direct amount of changes
Direct amount of topological gatherings
Einstein summation, an approach to contracting tensor files
Void total, an aggregate without any terms
Endless total, the converse of a limited contrast
Kronecker total, an activity thought about a sort of expansion for lattices
Framework expansion, in straight polynomial math
Minkowski expansion, an amount of two subsets of a vector space
Power aggregate symmetric polynomial, in commutative variable based math
Prefix aggregate, in processing
Pushout (classification hypothesis) (likewise called an amalgamated total or a cocartesian square, fibered coproduct, or fibered aggregate), the colimit of a chart comprising of two morphisms f : Z → X and g : Z → Y with a typical domainor pushout, prompting a fibered aggregate in classification hypothesis
QCD aggregate principles, in quantum field hypothesis
Riemann aggregate, in analytics
Rule of aggregate, in combinatorics
Subset aggregate issue, in cryptography
Aggregate rule in separation, in analytics
Aggregate rule in coordination, in math
Aggregate rule in quantum mechanics
Wedge total, a one-point association of topological spaces
Whitney aggregate, of fiber groups
Lose issue in combinatorics

Prefix sum

In computer science, the prefix sum, cumulative sum, inclusive scan, or simply scan of a sequence of numbers x₀, x₁, x₂, … is a second sequence of numbers y₀, y₁, y₂, …, the sums of prefixes (running totals) of the input sequence:

y₀ = x₀

y₁ = x₀ + x₁

y₂ = x₀ + x₁+ x₂

…

For instance, the prefix sums of the natural numbers are the triangular numbers:

input numbers	1	2	3	4	5	6	…
prefix sums	1	3	6	10	15	21	…

Prefix sums are trivial to compute in sequential models of computation, by using the formula y_i = y_{i − 1} + x_i to compute each output value in sequence order. However, despite their ease of computation, prefix sums are a useful primitive in certain algorithms such as counting sort, and they form the basis of the scan higher-order function in functional programming languages. Prefix sums have also been much studied in parallel algorithms, both as a test problem to be solved and as a useful primitive to be used as a subroutine in other parallel algorithms.

Abstractly, a prefix sum requires only a binary associative operator ⊕, making it useful for many applications from calculating well-separated pair decompositions of points to string processing.

Mathematically, the operation of taking prefix sums can be generalized from finite to infinite sequences; in that context, a prefix sum is known as a partial sum of a series. Prefix summation or partial summation form linear operators on the vector spaces of finite or infinite sequences; their inverses are finite difference operators.

Subset sum problem

The subset sum problem (SSP) is a decision problem in computer science. In its most general formulation, there is a multiset  of integers and a target-sum , and the question is to decide whether any subset of the integers sum to precisely .The problem is known to be NP-hard. Moreover, some restricted variants of it are NP-complete too, for example:

• The variant in which all inputs are positive.
• The variant in which inputs may be positive or negative, and . For example, given the set , the answer is yes because the subset  sums to zero.
• The variant in which all inputs are positive, and the target sum is exactly half the sum of all inputs, i.e., . This special case of SSP is known as the partition problem.

SSP can also be regarded as an optimization problem: find a subset whose sum is at most T, and subject to that, as close as possible to T. It is NP-hard, but there are several algorithms that can solve it reasonably quickly in practice.

SSP is a special case of the knapsack problem and of the multiple subset sum problem.

Summation

In math, summation is the expansion of a grouping of any sort of numbers, called addends or summands; the outcome is their aggregate or aggregate. Next to numbers, different sorts of values can be added also: capabilities, vectors, networks, polynomials and, as a general rule, components of a numerical items on which an activity indicated “+” is characterized.

Summations of limitless groupings are called series. They include the idea of breaking point, and are not viewed as in this article.

The summation of an express grouping is indicated as a progression of increases. For instance, summation of [1, 2, 4, 2] is signified 1 + 2 + 4 + 2, and results in 9, that is to say, 1 + 2 + 4 + 2 = 9. Since expansion is affiliated and commutative, there is no need of enclosures, and the outcome is the equivalent regardless of the request for the summands. Summation of a grouping of just a single component brings about this component itself. Summation of an unfilled grouping (a succession without any components), by show, brings about 0.

Frequently, the components of a grouping are characterized, through a standard example, as an element of their position in the succession. For straightforward examples, summation of long groupings might be addressed with most summands supplanted by circles. For instance, summation of the initial 100 regular numbers might be composed as 1 + 2 + 3 + 4 + ⋯ + 99 + 100. In any case, summation is meant by utilizing Σ documentation, where
∑ is an amplified capital Greek letter sigma. For instance, the amount of the principal n regular numbers can be signified as

For long summations, and summations of variable length (characterized with circles or Σ documentation), it is a typical issue to track down shut structure articulations for the outcome. For instance,

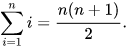
Albeit such equations don’t necessarily exist, numerous summation recipes have been found — with probably the most widely recognized and rudimentary ones being recorded in the rest of this article.

1 + 2 + 3 + 4 + ⋯

The endless series whose terms are the regular numbers 1 + 2 + 3 + 4 + ⋯ is a unique series. The nth halfway amount of the series is the three-sided number

which increments without bound as n goes to limitlessness. Since the succession of fractional aggregates neglects to join to a limited breaking point, the series doesn’t have an aggregate.

Albeit the series appears to be from the outset not to have any significant worth whatsoever, yielding various numerically intriguing results can be controlled. For instance, numerous summation strategies are utilized in science to dole out mathematical qualities even to a different series. Specifically, the techniques for zeta capability regularization and Ramanujan summation dole out the series a worth of −+1/12.,which is communicated by a well known formula

where the left-hand side must be deciphered just like the worth got by utilizing one of the previously mentioned summation techniques and not as the amount of an endless series in its standard significance. These techniques have applications in different fields, for example, complex examination, quantum field hypothesis, and string hypothesis.

In a monograph on home brew hypothesis, College of Alberta mathematician Terry Gannon refers to this situation as “perhaps of the most noteworthy equation in science”.

Ramanujan’s sum

In number hypothesis, Ramanujan’s total, typically meant cq(n), is a component of two positive number factors q and n characterized by the equation

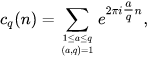
where (a, q) = 1 implies that a main takes on values coprime to q.

Srinivasa Ramanujan referenced the totals in a 1918 paper. notwithstanding the extensions examined in this article, Ramanujan’s aggregates are utilized in the evidence of Vinogradov’s hypothesis that each adequately enormous odd number is the amount of three primes.

Case Study on Sum

Certainly! Here is an example case study on how the sum function can be used in a business context:

Company XYZ is a large retail chain with multiple locations across the country. They are currently analyzing their sales data from the past quarter in order to identify trends and make informed decisions for the future. One important metric they are looking at is their total sales revenue for the quarter.

To calculate this, they use the sum function in Excel to add up the sales data for each individual store and get a grand total. They also use the sum function to calculate the average sales per store by dividing the total sales revenue by the number of stores. This helps them identify which stores are performing well and which ones may need additional support.

In addition to analyzing sales revenue, Company XYZ also uses the sum function to track expenses. They add up all of their expenses for the quarter, including rent, utilities, and employee salaries, in order to determine their net profit.

By using the sum function to analyze their financial data, Company XYZ is able to make informed decisions about where to focus their efforts and resources in order to improve their overall performance.

White paper on Sum

Here is a white paper on the sum function and its applications:

Introduction

The sum function is a commonly used mathematical operation that calculates the total value of a set of numbers. It is a basic operation in arithmetic and is widely used in various fields including finance, statistics, and engineering. In this white paper, we will discuss the properties of the sum function, its applications, and some best practices for using it effectively.

Properties of the Sum Function

The sum function takes a set of numbers as its input and returns their total value. It is denoted by the symbol ∑, which stands for “sum of.” The sum function has the following properties:

1. Commutativity: The order of the numbers in the set does not affect the result of the sum function. In other words, adding the numbers in a different order will give the same result.
2. Associativity: The sum of a set of numbers can be computed by grouping the numbers in any way and then adding them. For example, (a + b) + c = a + (b + c).
3. Distributivity: The sum function is distributive over multiplication. This means that the sum of the product of a number and a set of numbers is equal to the product of the number and the sum of the set of numbers. For example, a(b + c) = ab + ac.

Applications of the Sum Function

The sum function is a mathematical operation that adds together a set of numbers. It has many applications in various fields, including:

1. Mathematics: The sum function is fundamental in many branches of mathematics, including calculus, statistics, and number theory. It is used to calculate the total of a series of numbers, find the mean or average of a set of values, and determine the sum of the terms of a sequence.
2. Finance: In finance, the sum function is used to calculate the total of a series of payments or investments over time. For example, it can be used to calculate the total amount of interest paid on a loan.
3. Computer programming: The sum function is a commonly used function in programming languages such as Python, Java, and C++. It is used to calculate the total of a list or array of numbers, which can be useful in many different applications.
4. Data analysis: The sum function is used in data analysis to calculate the total of a set of data points. This can be used to find the total sales of a company, the total number of website visitors, or the total amount of rainfall in a particular region.
5. Physics: In physics, the sum function is used to calculate the total energy or force of a system. For example, it can be used to calculate the total gravitational force between two objects.

Overall, the sum function is a fundamental tool in many fields and has a wide range of applications.