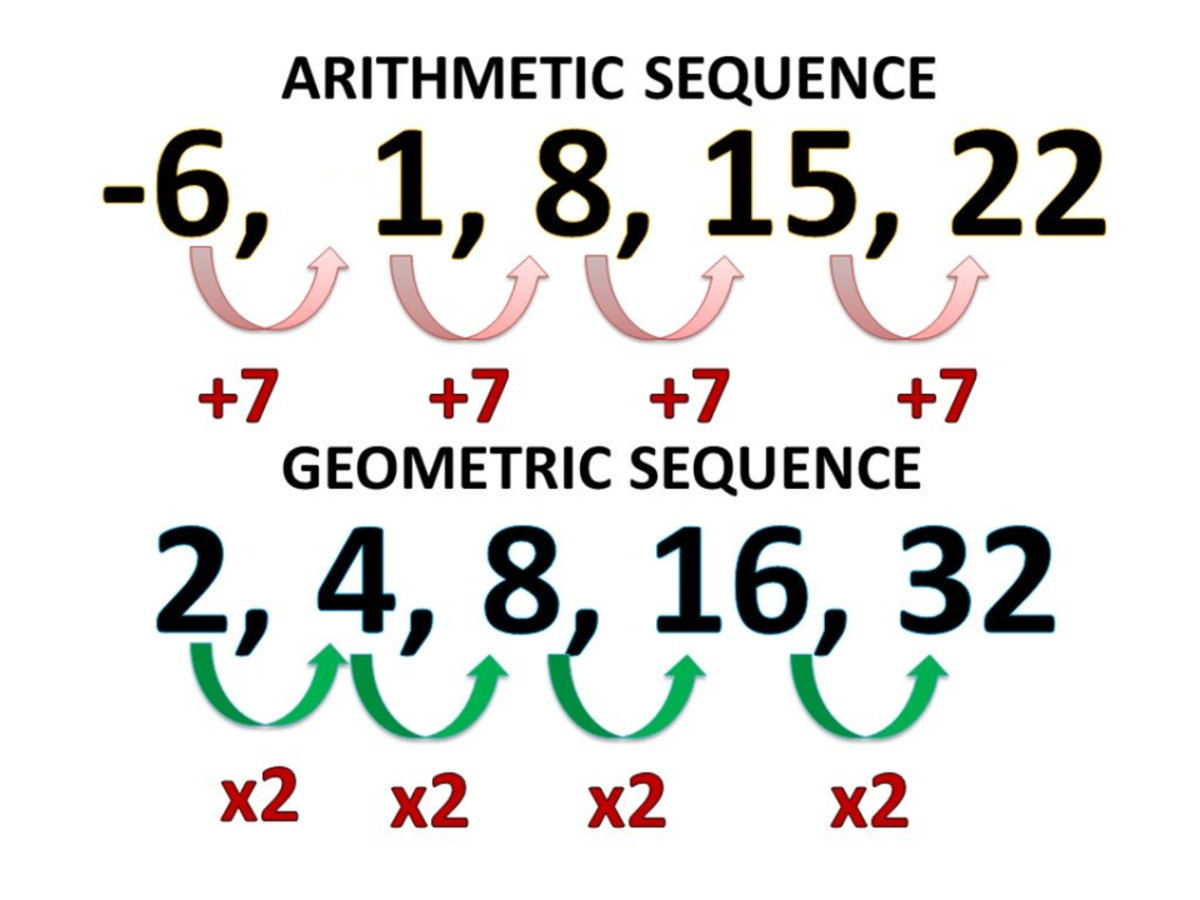
Arithmetic Progression: An arithmetic progression is a sequence of numbers in which each term is obtained by adding a fixed number to the preceding term. The fixed number is called the common difference. For example, the sequence 2, 4, 6, 8, 10 is an arithmetic progression with a common difference of 2.
The sum of the first n terms of an arithmetic progression can be found using the following formula:
S_n = (n/2) * [2a + (n-1)d]
where S_n is the sum of the first n terms, a is the first term, d is the common difference, and n is the number of terms.
Geometric Progression: A geometric progression is a sequence of numbers in which each term is obtained by multiplying the preceding term by a fixed number. The fixed number is called the common ratio. For example, the sequence 2, 4, 8, 16, 32 is a geometric progression with a common ratio of 2.
The sum of the first n terms of a geometric progression can be found using the following formula:
S_n = a(1 – r^n) / (1 – r)
where S_n is the sum of the first n terms, a is the first term, r is the common ratio, and n is the number of terms.
It’s important to note that for a geometric progression, the sum only exists if the common ratio is not equal to 1. If the common ratio is equal to 1, then the sequence is not a geometric progression, but rather a sequence of equal numbers.
It’s also worth noting that there are other types of progressions, such as harmonic progressions and Fibonacci sequences, which have their own formulas for calculating sums.
What is Required Sums of finite arithmetic and geometric progressions
The required algebraic sums of finite arithmetic and geometric progressions are the formulas used to find the sum of a given number of terms in an arithmetic or geometric progression.
For an arithmetic progression, the sum of the first n terms can be found using the formula:
S_n = (n/2) * [2a + (n-1)d]
where S_n is the sum of the first n terms, a is the first term, d is the common difference, and n is the number of terms.
For a geometric progression, the sum of the first n terms can be found using the formula:
S_n = a(1 – r^n) / (1 – r)
where S_n is the sum of the first n terms, a is the first term, r is the common ratio, and n is the number of terms.
These formulas are useful in many applications, such as calculating the total amount of interest earned on an investment that grows at a fixed rate each year, or determining the total distance traveled by a car that increases its speed by a fixed amount each second.
Who is Required Sums of finite arithmetic and geometric progressions
The algebraic sums of finite arithmetic and geometric progressions are required by anyone who needs to find the sum of a given number of terms in an arithmetic or geometric progression. These formulas are commonly used in various fields of mathematics, including algebra, calculus, and statistics.
In particular, these formulas are useful in solving real-world problems that involve arithmetic and geometric progressions. For example, in finance, these formulas can be used to calculate the total amount of interest earned on an investment that grows at a fixed rate each year. In physics, these formulas can be used to determine the total distance traveled by an object that moves with a fixed velocity or acceleration.
Students of mathematics, especially those studying algebra or calculus, also need to be familiar with these formulas, as they are often tested on them in exams and assignments. Additionally, anyone who works with data, such as statisticians or data analysts, may use these formulas to calculate various statistical measures, such as the mean or standard deviation, which can be expressed as sums of arithmetic or geometric progressions.
When is Required Sums of finite arithmetic and geometric progressions
The algebraic sums of finite arithmetic and geometric progressions are required whenever you need to find the sum of a given number of terms in an arithmetic or geometric progression. These formulas can be used in a wide range of situations, including:
- Finance: For example, when calculating the total interest earned on an investment that grows at a fixed rate each year, the formula for the sum of a geometric progression can be used.
- Physics: For example, when calculating the total distance traveled by an object that moves with a fixed velocity or acceleration, the formula for the sum of an arithmetic progression can be used.
- Engineering: For example, when calculating the total cost of a project that increases in cost by a fixed amount each year, the formula for the sum of an arithmetic progression can be used.
- Mathematics: The formulas for the sums of arithmetic and geometric progressions are important tools in algebra, calculus, and other areas of mathematics.
- Statistics: These formulas can be used to calculate various statistical measures, such as the mean or standard deviation, which can be expressed as sums of arithmetic or geometric progressions.
In general, anytime you need to find the sum of a series of numbers that follow a fixed pattern, the formulas for the sums of arithmetic and geometric progressions can be useful.
Where is Required Sums of finite arithmetic and geometric progressions
The algebraic sums of finite arithmetic and geometric progressions can be used in various fields and situations, including:
- Mathematics: These formulas are important tools in algebra, calculus, and other areas of mathematics. They can be used to find the sum of a given number of terms in a sequence that follows a fixed pattern.
- Finance: In finance, the formula for the sum of a geometric progression can be used to calculate the total interest earned on an investment that grows at a fixed rate each year.
- Physics: The formula for the sum of an arithmetic progression can be used in physics to calculate the total distance traveled by an object that moves with a fixed velocity or acceleration.
- Engineering: In engineering, the formula for the sum of an arithmetic progression can be used to calculate the total cost of a project that increases in cost by a fixed amount each year.
- Statistics: These formulas can be used to calculate various statistical measures, such as the mean or standard deviation, which can be expressed as sums of arithmetic or geometric progressions.
In summary, the algebraic sums of finite arithmetic and geometric progressions can be used in a wide range of fields and situations where a sequence of numbers follows a fixed pattern and its sum needs to be calculated.
How is Required Sums of finite arithmetic and geometric progressions
The algebraic sums of finite arithmetic and geometric progressions can be calculated using specific formulas.
For an arithmetic progression, the formula to find the sum of the first n terms is:
S_n = (n/2) * [2a + (n-1)d]
where S_n is the sum of the first n terms, a is the first term, d is the common difference, and n is the number of terms.
To use this formula, you need to know the first term of the arithmetic sequence, the common difference between consecutive terms, and the number of terms you want to sum.
For a geometric progression, the formula to find the sum of the first n terms is:
S_n = a(1 – r^n) / (1 – r)
where S_n is the sum of the first n terms, a is the first term, r is the common ratio, and n is the number of terms.
To use this formula, you need to know the first term of the geometric sequence, the common ratio between consecutive terms, and the number of terms you want to sum.
Once you have determined the values of a, d or r, and n, you can substitute them into the relevant formula and simplify to find the sum of the given sequence.
It is important to note that these formulas only work for finite arithmetic and geometric progressions, where there is a fixed number of terms to sum. For infinite progressions, more complex methods are required to determine the sum.
Case Study on Sums of finite arithmetic and geometric progressions
Case Study: Calculating the Sum of a Series of Payments
Sarah has taken out a loan to pay for her college tuition. The loan requires her to make 10 equal payments at the end of each month, with an annual interest rate of 8%. Sarah wants to know the total amount she will repay over the life of the loan, including interest. To calculate this, we can use the formula for the sum of a geometric progression.
Solution:
We first need to determine the payment amount, which can be calculated using the formula for the present value of an annuity:
PMT = (PV * i) / (1 – (1 + i)^-n)
where PMT is the payment amount, PV is the present value of the loan (i.e., the amount borrowed), i is the monthly interest rate (which is the annual interest rate divided by 12), and n is the number of payments (which is 10 in this case).
Assuming Sarah borrowed $10,000, we have:
i = 8% / 12 = 0.00667 n = 10 PV = $10,000
PMT = ($10,000 * 0.00667) / (1 – (1 + 0.00667)^-10) = $1,124.97
So, Sarah will need to make monthly payments of $1,124.97.
To calculate the total amount Sarah will repay over the life of the loan, we can use the formula for the sum of a geometric progression:
S_n = a(1 – r^n) / (1 – r)
where S_n is the sum of the first n terms, a is the first term (i.e., the payment amount), r is the common ratio (which is 1 in this case, since each payment is the same), and n is the number of terms (which is 10).
Substituting the values, we get:
S_10 = $1,124.97 * (1 – 1^10) / (1 – 1) = $11,249.70
So, Sarah will repay a total of $11,249.70 over the life of the loan, including interest.
White paper on Sums of finite arithmetic and geometric progressions
Introduction: Algebra Sums of finite arithmetic and geometric progressions are important tools in mathematics, finance, engineering, physics, and statistics. They allow us to calculate the sum of a given number of terms in a sequence that follows a fixed pattern. In this white paper, we will explore the concept of algebraic sums of finite arithmetic and geometric progressions, their formulas, and their applications.
Arithmetic Progressions: An arithmetic progression is a sequence of numbers in which each term is obtained by adding a fixed number to the previous term. The fixed number is called the common difference (d). The first term (a) and the common difference (d) completely determine the arithmetic sequence. For example, 1, 3, 5, 7, 9 is an arithmetic sequence where a = 1 and d = 2.
The formula to find the sum of the first n terms of an arithmetic sequence is:
S_n = (n/2) * [2a + (n-1)d]
where S_n is the sum of the first n terms, a is the first term, d is the common difference, and n is the number of terms. This formula can be derived using the method of mathematical induction.
Geometric Progressions: A geometric progression is a sequence of numbers in which each term is obtained by multiplying the previous term by a fixed number. The fixed number is called the common ratio (r). The first term (a) and the common ratio (r) completely determine the geometric sequence. For example, 2, 4, 8, 16, 32 is a geometric sequence where a = 2 and r = 2.
The formula to find the sum of the first n terms of a geometric sequence is:
S_n = a(1 – r^n) / (1 – r)
where S_n is the sum of the first n terms, a is the first term, r is the common ratio, and n is the number of terms. This formula can be derived using the formula for the sum of an infinite geometric series.
Applications: The algebraic sums of finite arithmetic and geometric progressions have numerous applications in various fields:
- Mathematics: These formulas are important tools in algebra, calculus, and other areas of mathematics. They can be used to find the sum of a given number of terms in a sequence that follows a fixed pattern.
- Finance: In finance, the formula for the sum of a geometric progression can be used to calculate the total interest earned on an investment that grows at a fixed rate each year.
- Physics: The formula for the sum of an arithmetic progression can be used in physics to calculate the total distance traveled by an object that moves with a fixed velocity or acceleration.
- Engineering: In engineering, the formula for the sum of an arithmetic progression can be used to calculate the total cost of a project that increases in cost by a fixed amount each year.
- Statistics: These formulas can be used to calculate various statistical measures, such as the mean or standard deviation, which can be expressed as sums of arithmetic or geometric progressions.
Conclusion: The algebraic sums of finite arithmetic and geometric progressions are important mathematical tools that have a wide range of applications. The formulas for calculating these sums are simple and easy to use, and can be applied in various fields. These formulas allow us to calculate the sum of a given number of terms in a sequence that follows a fixed pattern, making them useful in solving various mathematical and real-world problems.