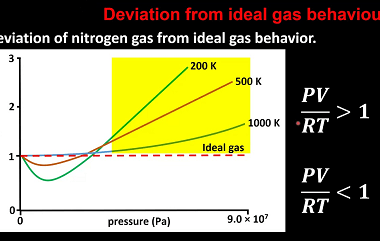
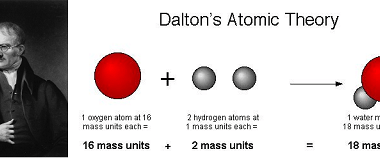
Deviation from ideality
In many fields, including physics, chemistry, and engineering, the concept of an ideal situation or system is often used as a theoretical or idealized benchmark for comparison with real-world situations. However, in practice, it is rare to encounter a situation that perfectly conforms to the ideal model. When a system deviates from the ideal model,…