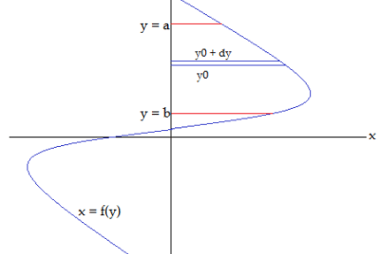
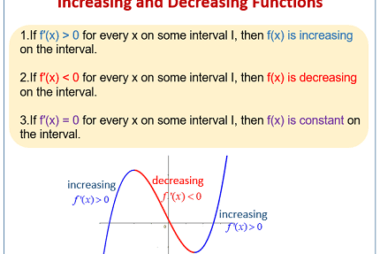
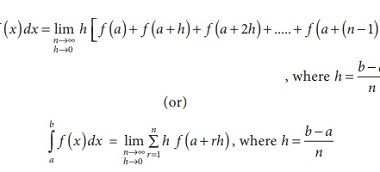Crash Course AIIMS-SYLLABUS Chemistry syllabus Electrolysis
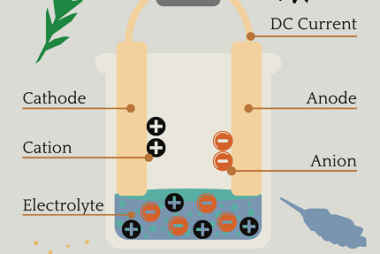
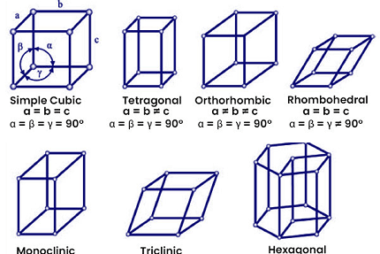
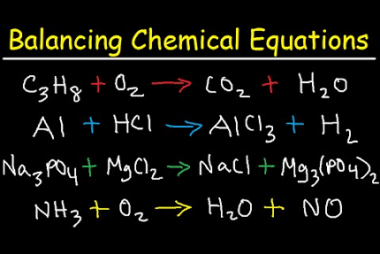
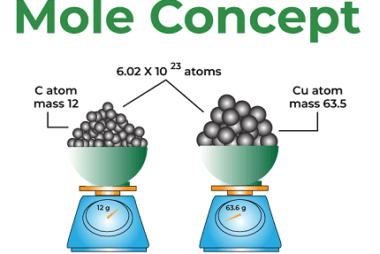
Electrolysis The syllabus for chemistry, specifically the topic of electrolysis, in the AIIMS (All India Institute of Medical Sciences) entrance exam may cover the following concepts: It’s important to note that syllabi can vary from year to year, so it’s recommended to consult the official AIIMS syllabus or the relevant study materials for the most…