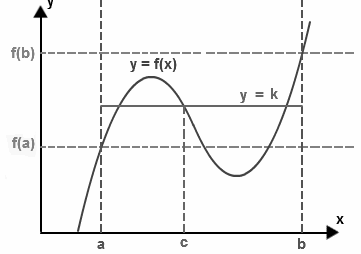
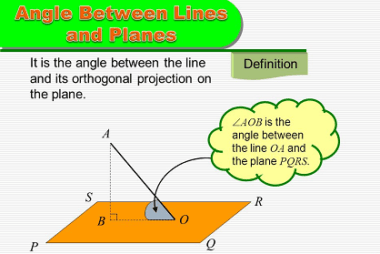
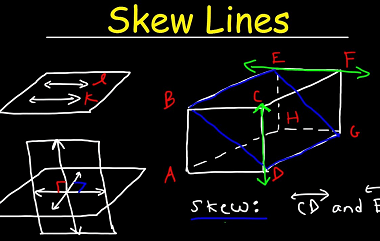
Derivatives of polynomial
The derivative of a polynomial is obtained by differentiating each term of the polynomial with respect to the variable. For example, let’s consider the polynomial: f(x) = 5x^3 + 2x^2 – 7x + 4 To find its derivative, we differentiate each term with respect to x: f'(x) = (d/dx)(5x^3) + (d/dx)(2x^2) – (d/dx)(7x) + (d/dx)(4)…