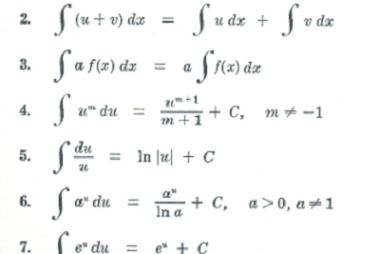Root mean square (RMS) velocity is a measure of the average speed of gas molecules in a sample at a given temperature. It is calculated as the square root of the average of the squares of the individual velocities of the molecules in the gas. Most probable velocity, on the other hand, is the speed…
Definite integrals can be used to determine the area bounded by a simple curve and the x-axis, or by a simple curve and the y-axis. The area can be found by dividing it into small rectangles, finding the area of each rectangle, and then adding up the areas of all the rectangles. This process is…
The fundamental theorem of calculus is a theorem that links the concept of differentiation with that of integration, and it has two parts. Part 1: Let f be a continuous function on the interval [a,b], and let F be a function defined by F(x) = ∫a^x f(t) dt where a ≤ x ≤ b. Then…
Sure, here are some common indefinite integrals of standard functions: Note that there are many more integrals of standard functions, but these are some of the most common ones. Also, the notation $\int f(x) dx$ represents the indefinite integral of the function $f(x)$ with respect to $x$, and $C$ is the constant of integration. What…
The derivative of a function f(x) gives the rate of change of f(x) with respect to x. The derivative of order two, or the second derivative of f(x), represents the rate of change of the first derivative of f(x) with respect to x. Mathematically, the second derivative of f(x) is denoted as f”(x) or d^2/dx^2…
Differential calculus is a branch of calculus that deals with the study of rates of change and slopes of curves. Trigonometry is a branch of mathematics that deals with the study of triangles and the relationships between their sides and angles. The two subjects are related in that trigonometric functions, such as sine, cosine, and…
Rationality refers to the ability to think logically, make sound judgments, and make decisions based on reason rather than emotions or impulses. It involves using critical thinking skills to analyze information, evaluate evidence, and draw conclusions based on facts and evidence. In general, a rational person is someone who can separate their emotions from their…
The derivative of a polynomial is obtained by differentiating each term of the polynomial with respect to the variable. For example, let’s consider the polynomial: f(x) = 5x^3 + 2x^2 – 7x + 4 To find its derivative, we differentiate each term with respect to x: f'(x) = (d/dx)(5x^3) + (d/dx)(2x^2) – (d/dx)(7x) + (d/dx)(4)…
Continuity is a fundamental concept in calculus that describes how a function behaves at every point in its domain. A function is said to be continuous if it has no abrupt jumps, breaks, or holes in its graph. More formally, a function f(x) is continuous at a point x=a if three conditions are met: If…
Coplanar lines are lines that lie on the same plane. In other words, any two points on each of the lines can be connected with a straight line that lies entirely in the same plane. For example, if two lines intersect, they are coplanar because the plane containing one line also contains the other line.…
