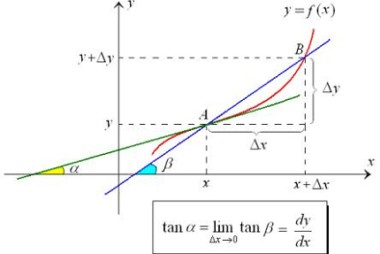
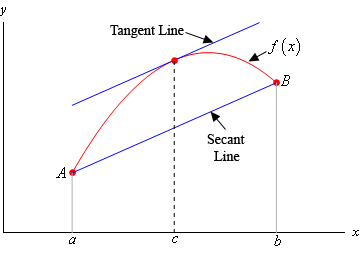
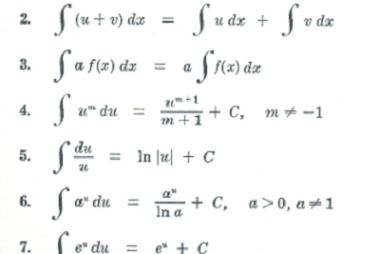When is Required – Page 50 – Vrindawan Coaching Center

Separation of variables method

Separation of variables is a method used to solve certain types of differential equations. The method involves assuming that the solution to the differential equation can be expressed as a product of two functions, each of which depends on only one of the variables in the equation. For example, consider the partial differential equation: ∂u/∂t…

April 1, 2023admin@coaching-center.inJEE Mathematics Integral Calculus, separation of variables methodBackground, Case Study on, How is Required, ordinary differential equation, Production of, Separation of variables method, When is Required, Where is Required

Formation of ordinary differential equations

Ordinary differential equations (ODEs) describe the relationships between a function and its derivatives with respect to a single independent variable. There are several ways to form ODEs, but some of the most common are: In general, the formation of ODEs requires an understanding of the underlying physical or mathematical principles that govern the system being…

April 1, 2023admin@coaching-center.inFormation of ordinary differential equations, JEE Mathematics Integral CalculusFormation of ordinary differential equations, How is Required, Mathematical Formulation of ODEs, ODE, Problem statement, When is Required, Where is Required, Who is Required

Application of definite integrals to the determination of areas bounded by simple curves

Definite integrals can be used to determine the area bounded by a simple curve and the x-axis, or by a simple curve and the y-axis. The area can be found by dividing it into small rectangles, finding the area of each rectangle, and then adding up the areas of all the rectangles. This process is…

April 1, 2023admin@coaching-center.inapplication of definite integrals to the determination of areas bounded by simple curves, JEE Mathematics Integral CalculusApplication of definite integrals to the determination of areas bounded by simple curves, Case Study on, Conclusion, Determine the limits of integration, What is Required, When is Required, White Paper on, Who is Required

Fundamental theorem of integral calculus

The fundamental theorem of calculus is a theorem that links the concept of differentiation with that of integration, and it has two parts. Part 1: Let f be a continuous function on the interval [a,b], and let F be a function defined by F(x) = ∫a^x f(t) dt where a ≤ x ≤ b. Then…

April 1, 2023admin@coaching-center.infundamental theorem of integral calculus, JEE Mathematics Integral CalculusCase Study on, Fundamental theorem of integral calculus, How is Required, Required Fundamental Theorem of Calculus, What is Required, When is Required, Where is Required, Who is Required

Definite integral and their properties

A definite integral is a mathematical concept that represents the area under a curve between two specified points on the x-axis. It is denoted by the symbol ∫, and is defined as: ∫[a,b] f(x) dx = F(b) – F(a) where f(x) is a function, F(x) is its antiderivative or indefinite integral, and a and b…

April 1, 2023admin@coaching-center.indefinite integral and their properties, JEE Mathematics Integral CalculusCase Study on, Definite integral and their properties, Definition, How is Required, Structures of, total accumulation, When is Required, Where is Required

Indefinite integrals of standard functions

Sure, here are some common indefinite integrals of standard functions: Note that there are many more integrals of standard functions, but these are some of the most common ones. Also, the notation $\int f(x) dx$ represents the indefinite integral of the function $f(x)$ with respect to $x$, and $C$ is the constant of integration. What…

April 1, 2023admin@coaching-center.inindefinite integrals of standard functions, JEE Mathematics Integral CalculusCalculating the, How is Required, Indefinite integrals of standard functions, What is Required, When is Required, Where is Required, White Paper, Who is Required

Integration as the inverse process of differentiation

Integration is the inverse process of differentiation. Differentiation is a process by which we find the rate of change of a function with respect to one of its variables. The inverse process of differentiation is integration, which is used to find the function that gives rise to a given rate of change. If we have…

April 1, 2023admin@coaching-center.inIntegration as the inverse process of differentiation, JEE Mathematics Integral Calculusamong others, Applications, Calculating the area under a curve, How is Required, Integration as the inverse process of differentiation, Integration Techniques, typically required, When is Required

Geometric interpretation of derivatives

The derivative of a function can be interpreted geometrically in several ways. One common interpretation is that the derivative represents the slope of the tangent line to the graph of the function at a given point. More specifically, if we consider a function f(x) and a point (a, f(a)) on its graph, the slope of…

April 1, 2023admin@coaching-center.ingeometric interpretation of derivatives, JEE Mathematics Differential Calculusdirection of motion, Geometric interpretation of derivatives, How is Required, Position Function and Instantaneous Velocity, When is Required, Where is Required, White Paper on, Who is Required

Derivatives up to order two of implicit functions

When dealing with implicit functions, we often have equations of the form: F(x, y) = 0 where y is an implicit function of x. That is, we can’t solve for y explicitly in terms of x. However, we can still differentiate the equation with respect to x to find the derivative of y with respect…

April 1, 2023admin@coaching-center.inderivatives up to order two of implicit functions, JEE Mathematics Differential CalculusCase Study on, Chain rule, Conclusion, Derivatives up to order two of implicit functions, How is Required, When is Required, Where is Required, Who is Required

Rolle’s theorem and Lagrange’s mean value theorem

Rolle’s Theorem and Lagrange’s Mean Value Theorem are two important results in calculus that relate to the behavior of functions on a given interval. Rolle’s Theorem states that if a function f(x) is continuous on the closed interval [a, b], differentiable on the open interval (a, b), and f(a) = f(b), then there exists at…

April 1, 2023admin@coaching-center.inJEE Mathematics Differential Calculus, Rolle’s theorem and Lagrange’s mean value theoremCase Study on, conditions must be satisfied, How is Required, important results in calculus, Joseph-Louis Lagrange, Rolle’s theorem and Lagrange’s mean value theorem, When is Required, White Paper on

Vrindawan Coaching Center

Padhega India Toh Badhega India

Tag: When is Required