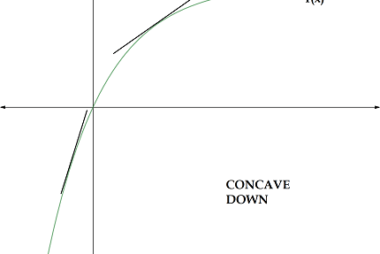
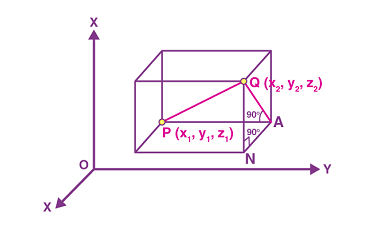
When is Required – Page 51 – Vrindawan Coaching Center

Derivatives of order two

The derivative of a function f(x) gives the rate of change of f(x) with respect to x. The derivative of order two, or the second derivative of f(x), represents the rate of change of the first derivative of f(x) with respect to x. Mathematically, the second derivative of f(x) is denoted as f”(x) or d^2/dx^2…

April 1, 2023admin@coaching-center.inderivatives of order two, JEE Mathematics Differential CalculusCase Study on, Derivatives of order two, How is Required, many others, What is Required, When is Required, Where is Required, White Paper on

Differential Calculus Trigonometric

Differential calculus is a branch of calculus that deals with the study of rates of change and slopes of curves. Trigonometry is a branch of mathematics that deals with the study of triangles and the relationships between their sides and angles. The two subjects are related in that trigonometric functions, such as sine, cosine, and…

April 1, 2023admin@coaching-center.inJEE Mathematics Differential Calculus, trigonometricCase Study on, Differential Calculus Trigonometric, How is Required, What is Required, When is Required, Where is Required, White Paper on, Who is Required

Chain rule

The chain rule is a fundamental rule in calculus that allows you to differentiate a function that is composed of two or more functions. More specifically, if you have a function f(x) that is composed of two functions g(x) and h(x), such that f(x) = g(h(x)), then the chain rule states that: f'(x) = g'(h(x))…

March 31, 2023admin@coaching-center.inchain rule, JEE Mathematics Differential CalculusChain rule, integration, Introduction, One practical application, optimization, problems in calculus, respect to x, When is Required

Derivative of the sum

Let f(x) and g(x) be two functions that are differentiable at x. The derivative of their sum, h(x) = f(x) + g(x), is given by: h'(x) = f'(x) + g'(x) In other words, to find the derivative of the sum of two functions, you simply take the derivatives of each function individually and add them…

March 31, 2023admin@coaching-center.inderivative of the sum, JEE Mathematics Differential CalculusDerivative of the sum, finite number of functions, four simpler functions, sum of two functions, Types of, When is Required, Where is Required, White Paper on

Coplanar lines

Coplanar lines are lines that lie on the same plane. In other words, any two points on each of the lines can be connected with a straight line that lies entirely in the same plane. For example, if two lines intersect, they are coplanar because the plane containing one line also contains the other line.…

March 31, 2023admin@coaching-center.incoplanar lines, JEE Mathematics Analytical GeometryCase Study on, Coplanar lines, How is Required, What is Required, When is Required, Where is Required, White Paper on, Who is Required

Skew lines

Skew lines are two non-intersecting lines that are not parallel to each other. In other words, skew lines are two lines in three-dimensional space that do not lie in the same plane and do not intersect each other. Skew lines are important in geometry and can be used to solve various problems, such as finding…

March 31, 2023admin@coaching-center.inJEE Mathematics Analytical Geometry, skew linesgeometry and skew, How is Required, p1 and p2, Properties and Applications, Skew lines, When is Required, Where is Required, Who is Required

Three dimensions: Distance between two points

The distance between two points in three-dimensional space can be found using the following formula: d = √((x2 – x1)^2 + (y2 – y1)^2 + (z2 – z1)^2) where (x1, y1, z1) and (x2, y2, z2) are the coordinates of the two points, and d is the distance between them. To use the formula, you…

March 30, 2023admin@coaching-center.inJEE Mathematics Analytical Geometry, Three dimensions: Distance between two pointsCase Study on, How is Required, Three dimensions: Distance between two points, What is Required, When is Required, Where is Required, White Paper on, Who is Required

Equation of a circle through the points of intersection of two circles and Those of a circle and A straight line

To find the equation of a circle passing through the points of intersection of two circles, we can follow these steps: Let’s say the two circles have equations: (x – a)^2 + (y – b)^2 = r^2 (x – c)^2 + (y – d)^2 = s^2 where (a,b) and (c,d) are the centers of the…

March 30, 2023admin@coaching-center.in1 Commentequation of a circle through the points of intersection of two circles and those of a circle and a straight line, JEE Mathematics Analytical GeometryCase Study on, Equation of a circle through the points of intersection of two circles and Those of a circle and A straight line, How is Required, What is Required, When is Required, Where is Required, White Paper on, Who is Required

Intersection of a circle with a straight line or a circle

The intersection of a circle and a straight line or a circle can take different forms depending on the relative positions and sizes of the objects involved. Intersection of a circle and a straight line: If a circle and a straight line lie in the same plane, they can intersect in three different ways: Intersection…

March 30, 2023admin@coaching-center.inintersection of a circle with a straight line or a circle, JEE Mathematics Analytical Geometryalgebra and geometry, b) and radius r, center (a, Intersection of a Circle and a Line in Robotics, Intersection of a circle with a straight line or a circle, Intersection of Two Circles, often studied in high school, real-world problems, When is Required

Equation of the bisector of the angle between two lines

Suppose we have two lines in a Cartesian coordinate system, given by the equations: a1x + b1y + c1 = 0a2x + b2y + c2 = 0 The angle between these two lines can be found using the formula: tan(theta) = |(m2 – m1)/(1 + m1*m2)| where m1 and m2 are the slopes of the…

March 29, 2023admin@coaching-center.inequation of the bisector of the angle between two lines, JEE Mathematics Analytical GeometryDetermining Rotation Direction of a 3D Object, Equation of the bisector of the angle between two lines, How is Required, Suppose we have two lines in the form of, When is Required, Where is Required, White Paper on, Who is Required

Vrindawan Coaching Center

Padhega India Toh Badhega India

Tag: When is Required