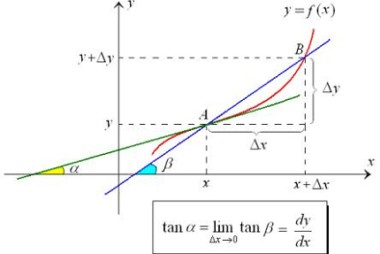
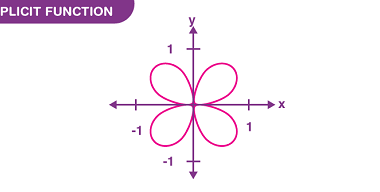
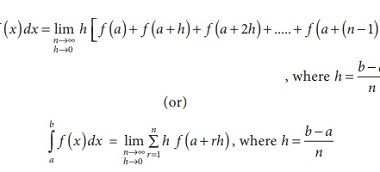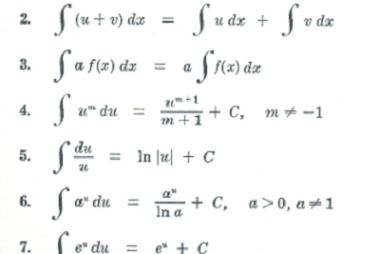Formation of ordinary differential equations
Ordinary differential equations (ODEs) describe the relationships between a function and its derivatives with respect to a single independent variable. There are several ways to form ODEs, but some of the most common are: In general, the formation of ODEs requires an understanding of the underlying physical or mathematical principles that govern the system being…