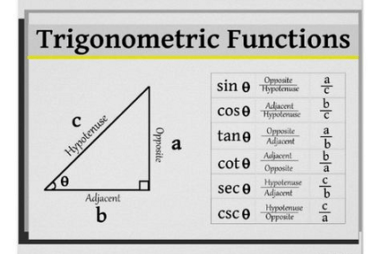
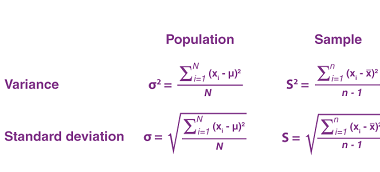Distance between two points
In analytical geometry, the distance between two points in a plane is given by the distance formula: d = sqrt((x2 – x1)^2 + (y2 – y1)^2) where (x1, y1) and (x2, y2) are the coordinates of the two points and d is the distance between them. To use the formula, simply substitute the values of…