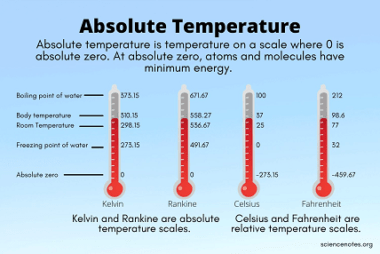
Absolute scale of temperature
The absolute scale of temperature is a temperature scale that starts at absolute zero, the theoretical lowest possible temperature where all matter would have zero thermal energy. The most commonly used absolute temperature scale is the Kelvin (K) scale, which is defined such that 0 K is equal to -273.15°C, the temperature at which all…