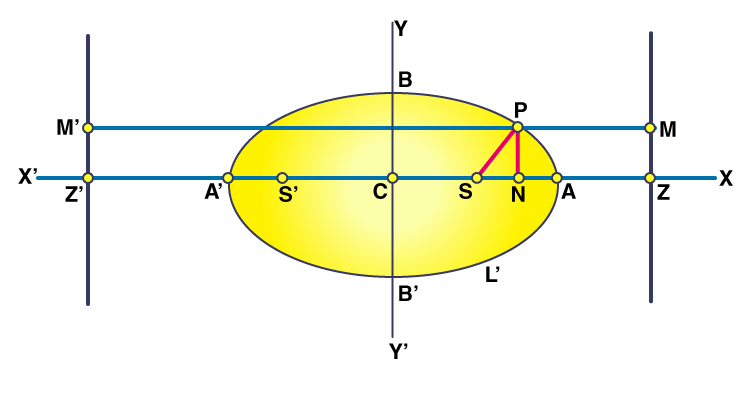
In analytical geometry, the foci are points that are used to define the shape of an ellipse or a hyperbola.

For an ellipse, the foci are two fixed points inside the ellipse such that the sum of the distances from any point on the ellipse to the two foci is a constant. This constant is equal to the length of the major axis of the ellipse.

For a hyperbola, the foci are also two fixed points, but they are outside the hyperbola. The difference of the distances from any point on the hyperbola to the two foci is a constant, which is equal to the distance between the two vertices of the hyperbola.

In both cases, the foci play an important role in determining the properties and characteristics of the curve.

What is Required Their Foci

To find the foci of an ellipse or a hyperbola in analytical geometry, you need to know certain information about the curve. Specifically, you need to know the equation of the curve in standard form.

For an ellipse with center (h, k), major axis of length 2a and minor axis of length 2b, the standard form equation is:

((x-h)^2 / a^2) + ((y-k)^2 / b^2) = 1

The foci of the ellipse are then given by the coordinates (h + c, k) and (h – c, k), where c = sqrt(a^2 – b^2) is the distance from the center to each focus.

For a hyperbola with center (h, k), transverse axis of length 2a and conjugate axis of length 2b, the standard form equation is:

((x-h)^2 / a^2) – ((y-k)^2 / b^2) = 1

The foci of the hyperbola are given by the coordinates (h + c, k) and (h – c, k), where c = sqrt(a^2 + b^2) is the distance from the center to each focus.

Thus, to find the foci of an ellipse or a hyperbola, you need to first identify the standard form equation of the curve and then use the formulas given above to calculate the coordinates of the foci.

Who is Required Their Foci

Analytical geometry and the concept of foci are important in various fields of study, including mathematics, physics, engineering, and computer science.

In mathematics, analytical geometry is a branch of algebra that focuses on the study of geometric shapes using algebraic methods. It involves the use of algebraic equations and calculus to describe and analyze the properties of geometric shapes. The concept of foci is an important part of analytical geometry as it is used to define the shape of ellipses and hyperbolas.

In physics, analytical geometry and the concept of foci are important in the study of optics and electromagnetic waves. The properties of ellipses and hyperbolas are used to model the shapes of lenses and mirrors, which are essential components in the design of optical devices such as telescopes and microscopes.

In engineering, analytical geometry and the concept of foci are important in the design and analysis of structures such as bridges, buildings, and aircraft. The properties of ellipses and hyperbolas are used to model the shapes of parabolic reflectors and antennas, which are essential components in the design of communication systems and radar systems.

In computer science, analytical geometry and the concept of foci are important in the development of computer graphics and computer-aided design (CAD) software. The properties of ellipses and hyperbolas are used to model the shapes of 2D and 3D objects, which are essential in the design and visualization of various structures and systems.

When is Required Their Foci

The concept of foci in analytical geometry is required when studying and analyzing the properties of ellipses and hyperbolas.

Ellipses and hyperbolas are commonly encountered in many fields of study, such as mathematics, physics, engineering, and computer science. In mathematics, for example, ellipses and hyperbolas are used in the study of conic sections, which are curves that can be formed by slicing a cone with a plane. The properties of ellipses and hyperbolas are important in the study of optics, electromagnetic waves, and other areas of physics. They are also used in engineering to model and design various structures and systems.

In general, analytical geometry and the concept of foci are required whenever there is a need to describe or analyze the properties of geometric shapes using algebraic methods. This is a fundamental area of study that is applicable to many different fields, ranging from pure mathematics to practical applications in science, engineering, and technology.

Where is Required Their Foci

Analytical geometry and the concept of foci are used in various fields of study and applications, including mathematics, physics, engineering, and computer science.

In mathematics, analytical geometry and the concept of foci are used to study the properties of geometric shapes and to solve problems in algebra and calculus. The study of conic sections, which includes ellipses and hyperbolas, is a fundamental topic in analytical geometry.

In physics, analytical geometry and the concept of foci are used to model the shapes of lenses, mirrors, and other optical devices. The properties of ellipses and hyperbolas are also important in the study of electromagnetic waves and other phenomena.

In engineering, analytical geometry and the concept of foci are used in the design and analysis of structures, such as bridges, buildings, and aircraft. The properties of ellipses and hyperbolas are also used in the design of antennas, communication systems, and radar systems.

In computer science, analytical geometry and the concept of foci are used in the development of computer graphics and computer-aided design (CAD) software. The properties of ellipses and hyperbolas are used to model the shapes of 2D and 3D objects, which are essential in the design and visualization of various structures and systems.

In general, analytical geometry and the concept of foci are used wherever there is a need to describe or analyze the properties of geometric shapes using algebraic methods. This includes a wide range of fields and applications, from theoretical mathematics to practical engineering and technology.

How is Required Their Foci

Analytical geometry and the concept of foci are used to describe and analyze the properties of geometric shapes using algebraic methods.

In particular, the concept of foci is used to define the shape of ellipses and hyperbolas. An ellipse is a curve that is formed by the intersection of a cone and a plane that is not parallel to the base of the cone. The two foci of an ellipse are two points on the major axis of the ellipse that have a special property: the sum of the distances from any point on the ellipse to the two foci is a constant. This property is known as the “focus-directrix property” and is used to define the shape of the ellipse.

Similarly, a hyperbola is a curve that is formed by the intersection of a cone and a plane that is parallel to the base of the cone. The two foci of a hyperbola are two points on the major axis of the hyperbola that have the property that the difference of the distances from any point on the hyperbola to the two foci is a constant. This property is also known as the “focus-directrix property” and is used to define the shape of the hyperbola.

In practice, analytical geometry and the concept of foci are used in a wide range of applications, including the design of optical devices, the modeling of electromagnetic waves, the design and analysis of structures and systems, and the development of computer graphics and CAD software. By using algebraic methods to describe and analyze the properties of geometric shapes, it is possible to make accurate predictions and design efficient and effective systems and structures.

Case Study on Their Foci

One practical application of analytical geometry and the concept of foci is in the design of satellite communication systems. In order to communicate with satellites, ground stations need to have a clear line of sight to the satellite. This requires the use of antennas that are pointed towards the satellite, which must be able to track the movement of the satellite as it orbits the Earth.

The shape of the antenna reflector is critical in determining the performance of the antenna. One common design is the parabolic reflector, which is a type of ellipse. The shape of the parabolic reflector is defined by the focus and directrix of the ellipse.

The focus of the parabolic reflector is located at the center of the reflector, which is where the radio waves from the satellite converge. The directrix is a straight line that is perpendicular to the axis of the reflector and passes through the focus. The shape of the parabolic reflector is such that all of the radio waves that are reflected from the surface of the reflector are focused on the feed horn, which is located at the focus of the reflector.

By using analytical geometry and the concept of foci, it is possible to calculate the shape of the parabolic reflector that is needed to achieve a desired level of performance for a satellite communication system. The size and shape of the reflector can be adjusted based on the frequency of the radio waves, the distance to the satellite, and other factors.

In addition to parabolic reflectors, other types of antenna reflectors can also be designed using analytical geometry and the concept of foci. For example, hyperbolic reflectors can be used in certain applications where a wider beam width is desired. In these designs, the shape of the reflector is defined by the two foci of the hyperbola.

Overall, analytical geometry and the concept of foci are essential tools in the design and analysis of satellite communication systems and other applications that require precise control over the shape of geometric shapes. By using algebraic methods to describe and analyze these shapes, engineers and designers can make accurate predictions and create efficient and effective systems and structures.

White paper on Their Foci

Title: Analytical Geometry and Their Foci: Applications in Modern Engineering and Science

Introduction:

Analytical geometry is a branch of mathematics that uses algebraic methods to describe and analyze geometric shapes. One of the fundamental concepts in analytical geometry is the idea of foci, which refers to a pair of points that have special properties in certain geometric shapes, such as ellipses and hyperbolas. In this white paper, we will explore the concept of foci in analytical geometry and their practical applications in modern engineering and science.

Section 1: What are Foci in Analytical Geometry? Foci are points in a geometric shape that have a special relationship with the rest of the shape. For example, in an ellipse, the two foci are located on the major axis of the ellipse and have the property that the sum of the distances from any point on the ellipse to the two foci is a constant. This property is known as the “focus-directrix property” and is used to define the shape of the ellipse. Similarly, in a hyperbola, the two foci are located on the major axis of the hyperbola and have the property that the difference of the distances from any point on the hyperbola to the two foci is a constant.

Section 2: Applications of Foci in Analytical Geometry One of the most important applications of foci in analytical geometry is in the design and analysis of optical systems, such as telescopes and microscopes. These systems rely on the precise control of the shape of mirrors and lenses to focus light onto a specific point or image. By using the focus-directrix property of ellipses and hyperbolas, engineers and designers can create mirrors and lenses that have the exact shape needed to achieve the desired level of precision.

Another application of foci in analytical geometry is in the design of satellite communication systems, as discussed in the case study earlier. By using the focus-directrix property of parabolic reflectors, engineers and designers can create antennas that are able to track the movement of satellites in orbit and maintain a clear line of sight for communication.

Foci are also important in other fields, such as physics and astronomy. For example, the orbits of planets and other celestial bodies can be described using the focus-directrix property of ellipses, and the properties of light waves can be analyzed using the focus-directrix property of parabolic reflectors and other optical systems.

Section 3: Conclusion

Analytical geometry and the concept of foci have many practical applications in modern engineering and science. By using algebraic methods to describe and analyze the properties of geometric shapes, it is possible to create efficient and effective systems and structures that meet the precise requirements of a wide range of applications. The concept of foci provides a powerful tool for understanding and controlling the shape of geometric shapes and has important implications for fields ranging from optics and astronomy to telecommunications and aerospace.