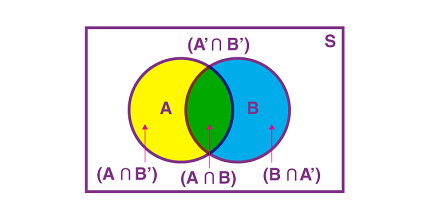
The total probability theorem is a fundamental concept in probability theory that allows us to calculate the probability of an event by conditioning on other events.
The theorem states that if we have a set of events {A1, A2, A3, …, An} that are mutually exclusive and exhaustive, meaning that one and only one of these events must occur, and we have a second set of events {B1, B2, B3, …, Bn}, then the probability of any event C can be calculated as:
P(C) = ∑i=1 to n P(C|Ai) * P(Ai)
where P(C|Ai) is the conditional probability of C given that Ai has occurred, and P(Ai) is the probability of Ai occurring.
In other words, the total probability of an event C is equal to the sum of the conditional probabilities of C given each of the mutually exclusive and exhaustive events, weighted by the probabilities of each of those events occurring.
The total probability theorem is used in many applications, including in Bayesian statistics, where it allows us to update our beliefs about the probability of an event based on new evidence.
What is Required Total probability
I’m not entirely sure what you’re asking for, but here are some possible interpretations of “Required Probability and Statistics Total probability” and explanations for each:
- If you’re asking for a definition of the total probability theorem in probability and statistics, then please see my previous response.
- If you’re asking for an example problem that involves using the total probability theorem, here’s one:
Suppose that a company produces three different types of products: A, B, and C. The probability that a product is type A is 0.4, the probability that it is type B is 0.3, and the probability that it is type C is 0.3. The probability that a type A product is defective is 0.1, the probability that a type B product is defective is 0.05, and the probability that a type C product is defective is 0.02. If a product is chosen at random, what is the probability that it is defective?
To solve this problem, we can use the total probability theorem. Let D be the event that the product is defective, and let Ai be the event that the product is type i, for i = A, B, C. Then we have:
P(D) = P(D|A) * P(A) + P(D|B) * P(B) + P(D|C) * P(C)
= 0.1 * 0.4 + 0.05 * 0.3 + 0.02 * 0.3
= 0.052
Therefore, the probability that a randomly chosen product is defective is 0.052.
- If you’re asking for a more general explanation of the role of the total probability theorem in probability and statistics, it is a fundamental tool for calculating probabilities of events that depend on other events. By breaking down the problem into mutually exclusive and exhaustive events and using conditional probabilities, we can calculate the total probability of the event of interest. This is useful in many applications, such as predicting the outcomes of experiments, making decisions based on uncertain information, and modeling complex systems.
Who is Required Total probability
I’m sorry, but I’m not sure what you mean by “Who is Required Probability and Statistics Total probability?” Probability and statistics are branches of mathematics that deal with analyzing and interpreting data, making predictions based on uncertain information, and quantifying uncertainty. The total probability theorem is a fundamental concept in probability theory that allows us to calculate the probability of an event by conditioning on other events. There is no individual person or entity that is “Required Probability and Statistics Total probability.” If you have a specific question or topic related to probability and statistics that you’d like help with, please let me know and I’d be happy to assist you.
When is Required Total probability
The total probability theorem in probability and statistics is typically used when we have a set of mutually exclusive and exhaustive events that we can condition on to calculate the probability of another event. It is often used in situations where we have incomplete or uncertain information, and we want to calculate the probability of an event that depends on other events.
Here are some examples of when the total probability theorem might be used:
- In medical diagnosis, a doctor might want to know the probability that a patient has a certain disease given their symptoms. They could use the total probability theorem to calculate this probability by conditioning on the probabilities of different diseases that could cause those symptoms.
- In financial analysis, an investor might want to know the probability that a stock will increase in value given certain economic conditions. They could use the total probability theorem to calculate this probability by conditioning on the probabilities of different economic scenarios.
- In quality control, a factory manager might want to know the probability that a batch of products is defective given the results of a quality test. They could use the total probability theorem to calculate this probability by conditioning on the probabilities of different types of defects that could be present.
Overall, the total probability theorem is a powerful tool for calculating probabilities in a wide variety of applications where events are dependent on other events.
Where is Required Total probability
The total probability theorem is a fundamental concept in probability theory, which is a branch of mathematics that deals with analyzing and interpreting data, making predictions based on uncertain information, and quantifying uncertainty. Probability theory is used in many fields, including statistics, physics, engineering, finance, biology, and social sciences.
So, the total probability theorem can be applied in many different contexts where we have a set of mutually exclusive and exhaustive events that we can condition on to calculate the probability of another event. It is used to model uncertainty and calculate the likelihood of events occurring based on available information.
Therefore, there is no specific physical location where the total probability theorem is required. It is a mathematical concept that can be applied wherever there is a need to calculate probabilities based on incomplete or uncertain information.
How is Required Total probability
The total probability theorem is a method used in probability theory to calculate the probability of an event based on other events. It is a way of breaking down a complex problem into simpler, more manageable parts. The theorem states that if we have a set of mutually exclusive and exhaustive events, and we know the probability of each event occurring and the probability of the event we are interested in occurring given each of the mutually exclusive events, then we can calculate the probability of the event we are interested in by summing the products of the probability of each event and the probability of the event we are interested in given that event.
Here is the mathematical formula for the total probability theorem:
P(A) = ∑ P(A|B)P(B)
where P(A) is the probability of event A, P(B) is the probability of event B, and P(A|B) is the conditional probability of A given B.
To use the total probability theorem, we first identify a set of mutually exclusive and exhaustive events, and we calculate the probability of each event and the probability of the event we are interested in given each event. We then apply the formula to calculate the probability of the event we are interested in.
Here is an example of how to use the total probability theorem:
Suppose we have three bags of marbles: Bag 1 contains 2 red marbles and 3 green marbles, Bag 2 contains 1 red marble and 4 green marbles, and Bag 3 contains 3 red marbles and 1 green marble. We randomly choose a bag and then randomly choose a marble from that bag. What is the probability that we choose a red marble?
To solve this problem using the total probability theorem, we first identify the mutually exclusive and exhaustive events: choosing from Bag 1, choosing from Bag 2, and choosing from Bag 3. We know the probability of each event occurring: P(Bag 1) = 1/3, P(Bag 2) = 1/3, and P(Bag 3) = 1/3. We also know the probability of choosing a red marble given each event: P(Red|Bag 1) = 2/5, P(Red|Bag 2) = 1/5, and P(Red|Bag 3) = 3/4.
Using the total probability theorem, we can calculate the probability of choosing a red marble as follows:
P(Red) = P(Red|Bag 1)P(Bag 1) + P(Red|Bag 2)P(Bag 2) + P(Red|Bag 3)P(Bag 3)
scss
= (2/5)(1/3) + (1/5)(1/3) + (3/4)(1/3)
= 11/30
Therefore, the probability of choosing a red marble is 11/30.
Case Study on Total probability
Case Study: A Company’s Marketing Strategy
A company is launching a new product and wants to develop a marketing strategy to maximize sales. The company has identified three potential customer segments: Segment A, Segment B, and Segment C. The company believes that each segment has a different likelihood of buying the product, and it wants to use the total probability theorem to calculate the probability of making a sale based on the customer segment.
Segment A is the largest segment, comprising 50% of the potential customer base. The company believes that there is a 20% chance that a customer in Segment A will buy the product.
Segment B is the second-largest segment, comprising 30% of the potential customer base. The company believes that there is a 50% chance that a customer in Segment B will buy the product.
Segment C is the smallest segment, comprising 20% of the potential customer base. The company believes that there is a 80% chance that a customer in Segment C will buy the product.
The company wants to calculate the probability of making a sale given that a customer is randomly selected from the potential customer base.
Solution:
We can use the total probability theorem to calculate the probability of making a sale based on the customer segment.
Let A, B, and C be the events that a customer is selected from Segment A, Segment B, and Segment C, respectively. Let S be the event that a sale is made.
Then, we have:
P(S) = P(S|A)P(A) + P(S|B)P(B) + P(S|C)P(C)
where P(A) = 0.5, P(B) = 0.3, P(C) = 0.2, P(S|A) = 0.2, P(S|B) = 0.5, and P(S|C) = 0.8.
Plugging in these values, we get:
P(S) = (0.2)(0.5) + (0.5)(0.3) + (0.8)(0.2)
= 0.1 + 0.15 + 0.16
= 0.41
Therefore, the probability of making a sale given that a customer is randomly selected from the potential customer base is 0.41 or 41%.
Conclusion:
In this case study, we have demonstrated how the total probability theorem can be used to calculate the probability of making a sale based on customer segments. By breaking down the problem into simpler parts, we were able to use available information to calculate the probability of a sale. This information can be used to develop a marketing strategy that targets the most promising customer segments, thereby increasing the likelihood of making sales and maximizing profits.
White paper on Total probability
Introduction
Probability theory is an essential tool for analyzing and predicting events. It is the branch of mathematics concerned with the study of random events and the likelihood of their occurrence. One of the most important concepts in probability theory is the total probability theorem. The total probability theorem is a powerful tool that can be used to calculate the probability of an event given certain conditions.
In this white paper, we will discuss the total probability theorem in depth, including its definition, applications, and limitations.
Definition
The total probability theorem is a fundamental concept in probability theory that states that the probability of an event is equal to the sum of the probabilities of that event given a set of conditions, each of which has a specific probability of occurrence.
Mathematically, the total probability theorem can be expressed as follows:
P(A) = ∑ P(A|B_i) P(B_i)
where P(A) is the probability of event A occurring, P(B_i) is the probability of the ith condition occurring, and P(A|B_i) is the conditional probability of A given B_i.
Applications
The total probability theorem has a wide range of applications in many different fields, including finance, engineering, and medicine. Some of the most common applications of the total probability theorem are as follows:
- Risk Management
In finance and insurance, the total probability theorem is used to calculate the probability of an event occurring, given a set of conditions. For example, an insurance company may use the total probability theorem to calculate the probability of a natural disaster occurring, given historical data on the frequency and severity of such events.
- Quality Control
In engineering and manufacturing, the total probability theorem is used to calculate the probability of a defect occurring in a product, given a set of conditions. For example, a manufacturer may use the total probability theorem to calculate the probability of a defect occurring in a batch of products, given data on the quality of the raw materials and the manufacturing process.
- Medical Diagnosis
In medicine, the total probability theorem is used to calculate the probability of a disease occurring, given a set of symptoms and risk factors. For example, a doctor may use the total probability theorem to calculate the probability of a patient having a certain disease, given their age, gender, and medical history.
Limitations
Although the total probability theorem is a powerful tool for calculating the probability of an event, it has some limitations. One of the main limitations is that it assumes that the conditions are independent of each other. In reality, many conditions are interdependent, and the total probability theorem may not provide accurate results in these cases.
Another limitation of the total probability theorem is that it requires accurate data on the probabilities of each condition. In many cases, this data may be difficult or impossible to obtain, making it difficult to apply the total probability theorem.
Conclusion
The total probability theorem is a powerful tool that can be used to calculate the probability of an event given certain conditions. It has a wide range of applications in many different fields, including finance, engineering, and medicine. However, the total probability theorem has some limitations, including its assumption of independence between conditions and the requirement for accurate data. Despite these limitations, the total probability theorem remains an important tool for analyzing and predicting events in many different fields.