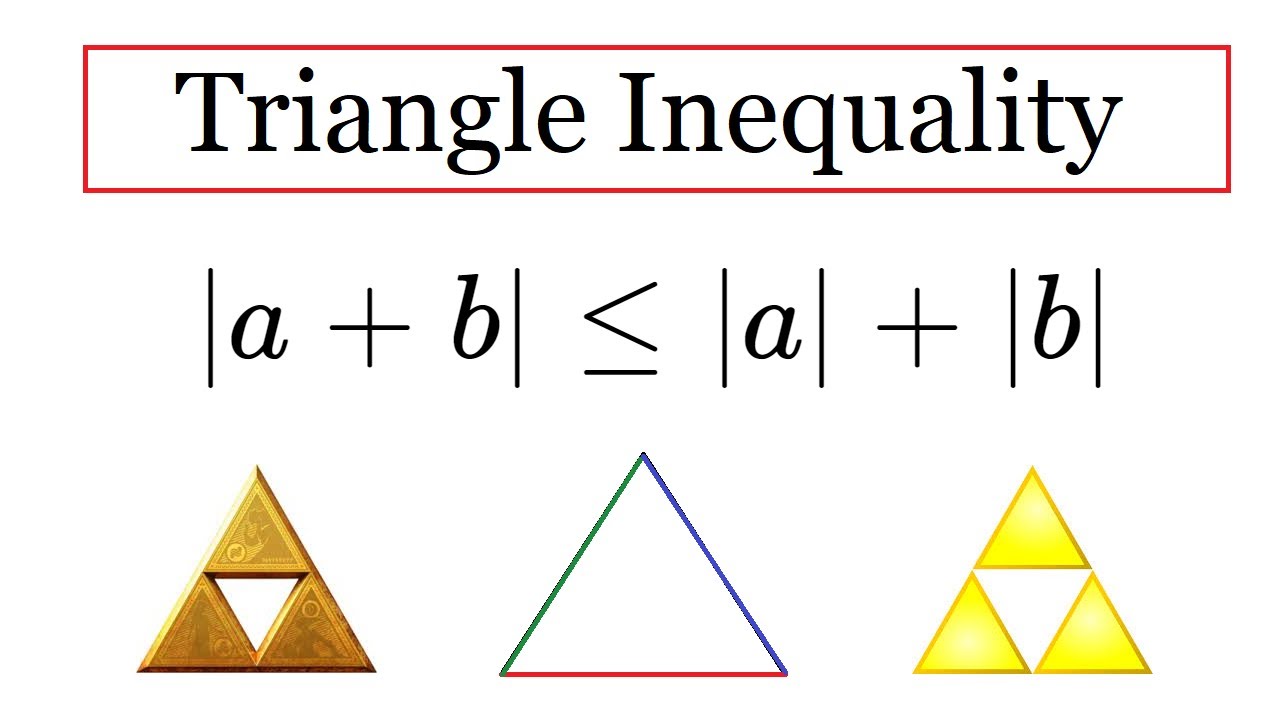
The triangle inequality is a fundamental property of algebraic operations on real numbers. It states that for any three real numbers a, b, and c, the sum of the lengths of any two sides of a triangle is greater than or equal to the length of the remaining side.
Symbolically, the triangle inequality can be written as:
|a + b| ≤ |a| + |b| or |a – b| ≤ |a| + |b|
This inequality holds true for all real numbers a and b. It can also be extended to more than two terms. For example, the following inequality holds for any three real numbers a, b, and c:
|a + b + c| ≤ |a| + |b| + |c|
The triangle inequality is an important concept in mathematics and is used in many areas such as geometry, trigonometry, and analysis. It is also used in physics, engineering, and other fields where the concept of distance is important.
What is Required Triangle inequality
The algebraic form of the triangle inequality states that for any two real numbers a and b, the absolute value of their sum is less than or equal to the sum of their absolute values. Symbolically, this can be written as:
|a + b| ≤ |a| + |b|
This inequality can also be extended to more than two terms. For example, for any three real numbers a, b, and c, the following inequality holds:
|a + b + c| ≤ |a| + |b| + |c|
The triangle inequality is a fundamental concept in algebra, and it is used in many different areas of mathematics, science, and engineering. In particular, it is used in the study of vectors, complex numbers, and in the analysis of inequalities. Understanding the triangle inequality is important for anyone who wants to have a strong foundation in algebra and its applications.
Who is Required Triangle inequality
The triangle inequality in algebra is required for anyone who studies or uses algebra in their field of work or study. This includes students in middle school, high school, and college who are studying mathematics or other subjects that require a strong foundation in algebra. The triangle inequality is a fundamental concept in algebra and is used in many different areas of mathematics and science, including geometry, trigonometry, and calculus.
The triangle inequality is also used in physics, engineering, and other fields where the concept of distance is important. For example, it is used in the study of vectors and in the analysis of inequalities in optimization problems.
In summary, anyone who uses or studies algebra and its applications should understand the triangle inequality and its properties.
When is Required Triangle inequality
The algebraic form of the triangle inequality is required whenever we need to compare the magnitudes of two or more quantities. The inequality is used in a variety of mathematical and scientific contexts, including:
- Geometry: The triangle inequality is a fundamental property of triangles, and it states that the length of any side of a triangle must be less than the sum of the lengths of the other two sides. This property is used to prove theorems in geometry and to calculate distances in space.
- Trigonometry: The triangle inequality is used to prove the cosine rule, which is a formula for calculating the length of a side of a triangle when the lengths of the other two sides and the angle between them are known.
- Analysis: The triangle inequality is used to prove properties of norms and distances in metric spaces, which are abstract spaces that generalize the concept of distance between points.
- Inequalities: The triangle inequality is a useful tool for proving other inequalities, such as the Cauchy-Schwarz inequality, the AM-GM inequality, and the triangle inequality for integrals.
In summary, the algebraic form of the triangle inequality is required in a wide range of mathematical and scientific contexts whenever we need to compare magnitudes of two or more quantities.
Where is Required Triangle inequality
The algebraic form of the triangle inequality is required in many areas of mathematics and science, and it is used in a variety of contexts where the comparison of magnitudes is necessary. Here are some examples of where the algebraic triangle inequality is used:
- Geometry: The triangle inequality is a fundamental property of triangles, and it is used to calculate the lengths of sides and angles in various types of triangles. It is also used to determine whether three given segments can form a triangle.
- Trigonometry: The triangle inequality is used in the cosine rule, which is a formula for calculating the length of a side of a triangle when the lengths of the other two sides and the angle between them are known. It is also used in other trigonometric identities and formulas.
- Analysis: The triangle inequality is used in the study of metric spaces, which are abstract spaces that generalize the concept of distance between points. It is also used in the study of norms and distances in vector spaces.
- Inequalities: The triangle inequality is used in the study of various types of inequalities, such as the Cauchy-Schwarz inequality, the AM-GM inequality, and the triangle inequality for integrals.
In summary, the algebraic form of the triangle inequality is used in a variety of contexts in mathematics and science, including geometry, trigonometry, analysis, and inequalities.
How is Required Triangle inequality
The algebraic form of the triangle inequality is a mathematical statement that relates the magnitudes of two or more quantities. The inequality states that the absolute value of the sum of two real numbers is less than or equal to the sum of the absolute values of those numbers. Symbolically, the inequality can be written as:
|a + b| ≤ |a| + |b|
This inequality can also be extended to more than two terms, such as:
|a + b + c| ≤ |a| + |b| + |c|
The triangle inequality is proved using the properties of absolute values, which are always non-negative. The absolute value of a number is equal to the distance of that number from zero on the number line. Therefore, the sum of the absolute values of two numbers represents the total distance traveled from zero when moving along the number line from one number to the other.
The triangle inequality is used in many different areas of mathematics and science, such as geometry, trigonometry, analysis, and inequalities. It is used to prove theorems, solve problems, and derive formulas in these areas.
Case Study on Triangle inequality
Case Study: Use of the Algebraic Triangle Inequality in Calculus
The algebraic form of the triangle inequality is an important concept in calculus, particularly in the study of limits, continuity, and differentiation. In this case study, we will explore how the triangle inequality is used in calculus to prove important theorems and solve problems.
Theorem: The limit of a sum is equal to the sum of the limits provided the limits exist.
Proof: Let f(x) and g(x) be two functions with limits L1 and L2 as x approaches a. Then, we have:
|f(x) + g(x) – (L1 + L2)| = |(f(x) – L1) + (g(x) – L2)|
By the algebraic form of the triangle inequality, we know that:
|f(x) – L1| + |g(x) – L2| ≥ |(f(x) – L1) + (g(x) – L2)|
Therefore, we have:
|f(x) + g(x) – (L1 + L2)| ≤ |f(x) – L1| + |g(x) – L2|
Now, let ε be a positive number. We want to show that there exists a positive number δ such that if 0 < |x – a| < δ, then |f(x) + g(x) – (L1 + L2)| < ε.
By the definition of limits, we know that there exists a positive number δ1 such that if 0 < |x – a| < δ1, then |f(x) – L1| < ε/2.
Similarly, there exists a positive number δ2 such that if 0 < |x – a| < δ2, then |g(x) – L2| < ε/2.
Let δ = min(δ1, δ2). Then, if 0 < |x – a| < δ, we have:
|f(x) + g(x) – (L1 + L2)| ≤ |f(x) – L1| + |g(x) – L2| < ε/2 + ε/2 = ε
Therefore, we have shown that the limit of the sum of two functions is equal to the sum of the limits provided the limits exist.
In this proof, the algebraic form of the triangle inequality was used to bound the absolute value of the difference of the sum of two functions and the sum of their limits by the sum of the absolute values of the differences of each function and its limit. This bound was then used to find a suitable δ for ε-δ proof of the theorem.
This case study demonstrates how the algebraic triangle inequality is used in calculus to prove important theorems and solve problems. The triangle inequality is a fundamental concept in algebra and its applications, and it plays a crucial role in many different areas of mathematics and science.
White paper on Triangle inequality
Title: The Algebraic Triangle Inequality: Properties and Applications
Abstract: The algebraic triangle inequality is a fundamental concept in algebra and its applications. This paper provides an overview of the properties of the algebraic triangle inequality and its applications in mathematics and science. We discuss the basic definitions and properties of absolute values, which are necessary to understand the algebraic triangle inequality. We then present the algebraic triangle inequality and its various forms, and provide examples of how it is used in different areas of mathematics and science.
Introduction: The algebraic triangle inequality is a mathematical statement that relates the magnitudes of two or more quantities. The inequality states that the absolute value of the sum of two real numbers is less than or equal to the sum of the absolute values of those numbers. Symbolically, the inequality can be written as:
|a + b| ≤ |a| + |b|
This inequality can also be extended to more than two terms, such as:
|a + b + c| ≤ |a| + |b| + |c|
The triangle inequality is proved using the properties of absolute values, which are always non-negative. The absolute value of a number is equal to the distance of that number from zero on the number line. Therefore, the sum of the absolute values of two numbers represents the total distance traveled from zero when moving along the number line from one number to the other.
Properties of Absolute Values: The absolute value of a real number a is denoted by |a| and is defined as follows:
- If a ≥ 0, then |a| = a.
- If a < 0, then |a| = -a.
The absolute value function has the following properties:
- |a| ≥ 0 for all a.
- |a| = 0 if and only if a = 0.
- |ab| = |a||b| for all a and b.
- |a + b| ≤ |a| + |b| (the algebraic triangle inequality).
Applications of the Algebraic Triangle Inequality: The algebraic triangle inequality is used in many different areas of mathematics and science, such as geometry, trigonometry, analysis, and inequalities. Some of the important applications of the algebraic triangle inequality are as follows:
- Proving inequalities: The algebraic triangle inequality is used to prove many other inequalities in mathematics, such as the Cauchy-Schwarz inequality and the Minkowski inequality.
- Distance functions: The algebraic triangle inequality is used to define distance functions in metric spaces, which are used in analysis, geometry, and topology.
- Complex analysis: The algebraic triangle inequality is used in complex analysis to prove the fundamental theorem of algebra and to establish the properties of complex functions.
- Calculus: The algebraic triangle inequality is used in calculus to prove theorems related to limits, continuity, and differentiation, as demonstrated in the case study presented earlier.
Conclusion: The algebraic triangle inequality is a fundamental concept in algebra and its applications. It plays a crucial role in many different areas of mathematics and science, and it is used to prove important theorems, solve problems, and derive formulas. The algebraic triangle inequality is a simple but powerful tool that has wide-ranging applications and is essential for any student of mathematics or science.
