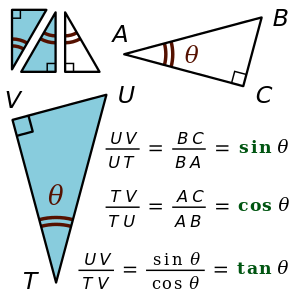
Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles. It is a fundamental tool in many areas of science and engineering, including physics, astronomy, and navigation.

The three primary trigonometric functions are sine, cosine, and tangent. These functions are defined based on the ratios of the lengths of the sides of a right triangle. In a right triangle, the side opposite the right angle is called the hypotenuse, and the other two sides are called the adjacent and opposite sides.

The sine function is defined as the ratio of the length of the opposite side to the length of the hypotenuse, while the cosine function is defined as the ratio of the length of the adjacent side to the length of the hypotenuse. The tangent function is defined as the ratio of the length of the opposite side to the length of the adjacent side.

Other trigonometric functions include cosecant (the reciprocal of sine), secant (the reciprocal of cosine), and cotangent (the reciprocal of tangent).

Trigonometry is used in a wide range of applications, such as calculating distances and angles in surveying, modeling wave behavior in physics, and analyzing the movement of celestial bodies in astronomy.

Trigonometric functions

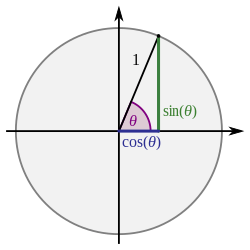
In science, the geometrical capabilities (likewise called roundabout capabilities, point capabilities or goniometric functions) are genuine capabilities which relate a point of a right-calculated triangle to proportions of two side lengths. They are broadly utilized in all sciences that are connected with math, like route, strong mechanics, heavenly mechanics, geodesy, and numerous others. They are among the easiest occasional capabilities, and as such are likewise broadly utilized for concentrating on intermittent peculiarities through Fourier examination.

The geometrical capabilities most generally utilized in current arithmetic are the sine, the cosine, and the digression. Their reciprocals are individually the cosecant, the secant, and the cotangent, which are less utilized. Every one of these six geometrical capabilities has a relating converse capability, and a simple among the exaggerated capabilities.

The most seasoned meanings of geometrical capabilities, connected with right-point triangles, characterize them just for intense points. To broaden the sine and cosine capabilities to capabilities whose space is the entire genuine line, mathematical definitions utilizing the standard unit circle (i.e., a circle with sweep 1 unit) are frequently utilized; then, at that point, the area of different capabilities is the genuine line for certain confined focuses eliminated. Current definitions express mathematical capabilities as limitless series or as arrangements of differential conditions. This permits expanding the area of sine and cosine capabilities to the entire complex plane, and the space of the other geometrical capabilities to the complicated plane for certain separated focuses eliminated.

List of trigonometric identities

In geometry, geometrical characters are equities that include mathematical capabilities and are valid for each worth of the happening factors for which the two sides of the equity are characterized. Mathematically, these are characters including specific elements of at least one points. They are unmistakable from triangle personalities, which are characters possibly including points yet additionally including side lengths or different lengths of a triangle.

These personalities are helpful while articulations including geometrical capabilities should be streamlined. A significant application is the mix of non-geometrical capabilities: a typical method includes first utilizing the replacement rule with a mathematical capability, and afterward improving on the subsequent necessary with a mathematical character.

Overview and definitions

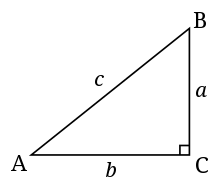
Trigonometry uses a large number of specific words to describe parts of a triangle. Some of the definitions in trigonometry are:

• Right-angled triangle – A right-angled triangle is a triangle that has an angle equal to 90 degrees. (A triangle cannot have more than one right angle) The standard trigonometric ratios can only be used on right-angled triangles.
• Hypotenuse – The hypotenuse of a triangle is the longest side, and the side that is opposite the right angle. For example, for the triangle on the right, the hypotenuse is side c.
• Opposite of an angle – The opposite side of an angle is the side that does not intersect with the vertex of the angle. For example, side a is the opposite of angle A in the triangle to the right.
• Adjacent of an angle – The adjacent side of an angle is the side that intersects the vertex of the angle but is not the hypotenuse. For example, side b is adjacent to angle A in the triangle to the right.

Trigonometric ratios

There are three main trigonometric ratios for right triangles, and three reciprocals of those ratios, making up a total of 6 ratios. They are:

• Sine (sin) – The sine of an angle is equal to the .
• Cosine (cos) – The cosine of an angle is equal to the .
• Tangent (tan) – The tangent of an angle is equal to the .

The reciprocals of these ratios are:

Cosecant (cosec) – The cosecant of an angle is equal to the  or .

Secant (sec) – The secant of an angle is equal to the  or .

Cotangent (cot) – The cotangent of an angle is equal to the  or .

Students often use a mnemonic to remember this relationship. The sine, cosine, and tangent ratios in a right triangle can be remembered by representing them as strings of letters, such as SOH-CAH-TOA:

Sine = Opposite ÷ Hypotenuse

Cosine = Adjacent ÷ Hypotenuse

Tangent = Opposite ÷ Adjacent

Proofs of trigonometric identities

There are a few identical ways for characterizing geometrical capabilities, and the evidence of the mathematical personalities between them rely upon the picked definition. The most established and some way or another the most rudimentary definition depends on the calculation of right triangles. The confirmations given in this article utilize this definition, and subsequently apply to non-negative points not more prominent than a right point. For more prominent and negative points, see Mathematical capabilities.

Different definitions, and subsequently different evidences depend on the Taylor series of sine and cosine, or on the differential condition f”+f=0 to which they are arrangements.

Spherical trigonometry

Circular geometry is the part of round math that arrangements with the metrical connections between the sides and points of circular triangles, generally communicated utilizing geometrical capabilities. On the circle, geodesics are extraordinary circles. Circular geometry is critical for estimations in cosmology, geodesy, and route.

The beginnings of round geometry in Greek science and the significant improvements in Islamic math are talked about completely in History of geometry and Math in archaic Islam. The subject happened as expected in Early Current times with significant improvements by John Napier, Delambre and others, and accomplished a basically complete structure toward the finish of the nineteenth 100 years with the distribution of Todhunter’s course reading Round geometry for the utilization of universities and Schools. From that point forward, huge advancements have been the use of vector techniques, quaternion strategies, and the utilization of mathematical techniques.

White paper on trigonometric

I can provide you with a brief introduction to trigonometry, but I’m not sure what you mean by a “white paper on trigonometric.” A white paper is a report or guide that explains a complex topic in a clear and concise manner, but it is usually focused on a specific industry, technology, or product. If you can provide me with more information on what you are looking for, I can try my best to help you.

Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles. It is a fundamental tool in many areas of science and engineering, including physics, astronomy, and navigation. The three primary trigonometric functions are sine, cosine, and tangent, which are defined based on the ratios of the lengths of the sides of a right triangle.

Trigonometry is used in a wide range of applications, such as calculating distances and angles in surveying, modeling wave behavior in physics, and analyzing the movement of celestial bodies in astronomy. It is also used in engineering to calculate the forces and stresses in structures and machinery.

The study of trigonometry involves understanding the properties and relationships of triangles, as well as learning to apply trigonometric functions and identities to solve problems. This includes topics such as angles, radians, the unit circle, trigonometric ratios, inverse trigonometric functions, and trigonometric equations and identities.

Overall, trigonometry is a powerful tool that plays a critical role in many scientific and engineering fields, and it is essential for anyone pursuing a career in these areas to have a solid understanding of its concepts and applications.