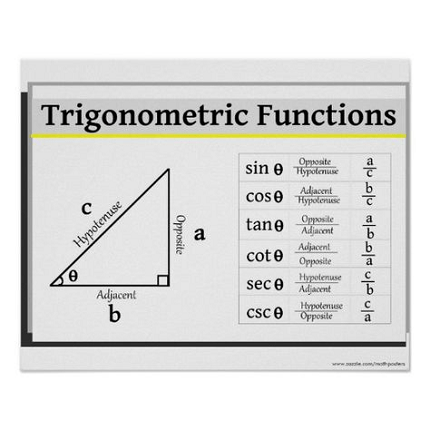
Trigonometric functions are mathematical functions that relate the angles of a right triangle to the lengths of its sides. The most commonly used trigonometric functions are sine (sin), cosine (cos), and tangent (tan). These functions can be defined in terms of the sides of a right triangle as follows:
- Sine (sin): The sine of an angle is the ratio of the length of the side opposite the angle to the length of the hypotenuse. It is denoted by sin θ, where θ is the angle. Thus, sin θ = opposite/hypotenuse.
- Cosine (cos): The cosine of an angle is the ratio of the length of the adjacent side to the length of the hypotenuse. It is denoted by cos θ, where θ is the angle. Thus, cos θ = adjacent/hypotenuse.
- Tangent (tan): The tangent of an angle is the ratio of the length of the side opposite the angle to the length of the adjacent side. It is denoted by tan θ, where θ is the angle. Thus, tan θ = opposite/adjacent.
In addition to these three functions, there are also three reciprocal trigonometric functions: cosecant (csc), secant (sec), and cotangent (cot). These functions are the reciprocals of the sine, cosine, and tangent functions, respectively:
- Cosecant (csc): The cosecant of an angle is the reciprocal of the sine of the angle. It is denoted by csc θ, where θ is the angle. Thus, csc θ = 1/sin θ.
- Secant (sec): The secant of an angle is the reciprocal of the cosine of the angle. It is denoted by sec θ, where θ is the angle. Thus, sec θ = 1/cos θ.
- Cotangent (cot): The cotangent of an angle is the reciprocal of the tangent of the angle. It is denoted by cot θ, where θ is the angle. Thus, cot θ = 1/tan θ.
What is Required Trigonometric functions
The Required Trigonometric functions depend on the problem or situation at hand. Generally, the most commonly used trigonometric functions in mathematics and science are sine (sin), cosine (cos), and tangent (tan). These functions are used to solve problems involving right triangles, such as finding the length of a side or the measure of an angle.
In addition to these three functions, the reciprocal trigonometric functions – cosecant (csc), secant (sec), and cotangent (cot) – can also be useful in solving certain problems.
Other trigonometric functions include the inverse trigonometric functions, which are used to find the angle given the ratio of the sides. These functions include inverse sine (sin⁻¹), inverse cosine (cos⁻¹), and inverse tangent (tan⁻¹).
Trigonometric functions also have applications in physics, engineering, and other fields, such as the study of waves and oscillations, and in the analysis of periodic phenomena such as sound waves and electromagnetic waves.
Who is Required Trigonometric functions
Trigonometric functions are required in various fields such as mathematics, physics, engineering, and many other scientific fields. They are also used in real-world applications such as navigation, architecture, surveying, and more.
In mathematics, trigonometric functions are used to solve problems involving triangles, waves, and periodic functions. They are also used in calculus, differential equations, and other advanced mathematical topics.
In physics, trigonometric functions are used to study waves, oscillations, and vibrations, and to analyze the behavior of physical systems that exhibit periodic behavior, such as pendulums and springs.
In engineering, trigonometric functions are used in various applications, such as the design of structures and machines, control systems, and electrical circuits.
Overall, trigonometric functions are an important tool in many fields and are essential for solving a wide range of problems in mathematics and science.
When is Required Trigonometric functions
Trigonometric functions are used whenever there is a need to relate angles to the sides of a right triangle, or when dealing with periodic functions and waves. Here are some examples of when trigonometric functions are required:
- Geometry: Trigonometric functions are used to solve problems involving angles and sides of a triangle. For example, finding the length of a side of a triangle given an angle and another side length, or finding the angle between two sides of a triangle given their lengths.
- Navigation: Trigonometric functions are used in navigation to determine the direction and distance between two points. For example, using the sine and cosine functions to determine the latitude and longitude of a location.
- Physics: Trigonometric functions are used in physics to analyze the behavior of waves and oscillations. For example, the sine and cosine functions are used to describe the displacement of a wave at a particular point in space and time.
- Engineering: Trigonometric functions are used in engineering to design and analyze structures, machines, and control systems. For example, the tangent function is used in electrical engineering to calculate the phase angle of an AC circuit.
- Sound and Music: Trigonometric functions are used in the study of sound and music to describe the waveform of a sound wave. For example, the sine function is used to describe the shape of a simple harmonic wave.
Overall, trigonometric functions are required whenever there is a need to relate angles to the sides of a triangle or when dealing with periodic functions and waves.
Where is Required Trigonometric functions
Trigonometric functions are used in various fields and applications, including:
- Mathematics: Trigonometric functions are a fundamental part of trigonometry, which is a branch of mathematics that deals with the relationships between the angles and sides of triangles. They are used in a wide range of mathematical topics, including calculus, differential equations, and complex analysis.
- Physics: Trigonometric functions are used in physics to study waves, oscillations, and vibrations, and to analyze the behavior of physical systems that exhibit periodic behavior, such as pendulums and springs.
- Engineering: Trigonometric functions are used in engineering to design and analyze structures, machines, and control systems. They are also used in electrical engineering to analyze AC circuits and in civil engineering to calculate angles and distances in surveying.
- Navigation: Trigonometric functions are used in navigation to determine the direction and distance between two points. They are also used in satellite navigation systems to determine the position of a receiver.
- Architecture: Trigonometric functions are used in architecture to calculate angles and distances when designing buildings and structures.
- Art and Design: Trigonometric functions are used in art and design to create curves and shapes. They are also used in computer graphics to create 3D models and animations.
Overall, trigonometric functions are used in a wide range of fields and applications, wherever there is a need to relate angles to the sides of a triangle or when dealing with periodic functions and waves.
How is Required Trigonometric functions
Trigonometric functions are mathematical functions that relate angles to the sides of a right triangle. The three primary trigonometric functions are sine, cosine, and tangent, which are commonly denoted as sin, cos, and tan, respectively.
The sine function (sin) relates the ratio of the length of the side opposite to an angle and the length of the hypotenuse of a right triangle. The cosine function (cos) relates the ratio of the length of the adjacent side and the hypotenuse of a right triangle. The tangent function (tan) relates the ratio of the length of the opposite side and the adjacent side of a right triangle.
Other trigonometric functions, such as the cosecant (csc), secant (sec), and cotangent (cot), are reciprocals of the sine, cosine, and tangent functions, respectively.
Trigonometric functions can be defined using the unit circle, which is a circle of radius 1 centered at the origin of a coordinate plane. The coordinates of a point on the unit circle can be used to calculate the values of sine and cosine functions, and the tangent function can be defined as the ratio of the sine and cosine functions.
Trigonometric functions have many properties, including periodicity, symmetry, and relationships between them, such as the Pythagorean identity and the sum and difference formulas.
Overall, trigonometric functions are used to solve problems involving angles and sides of a right triangle, and they have many applications in mathematics, science, and engineering.
Case Study on Trigonometric functions
Case Study: Using Trigonometric Functions in Architecture
Trigonometric functions are widely used in architecture to calculate angles and distances when designing buildings and structures. In this case study, we will explore how trigonometric functions were used to design a modern building.
The Challenge: An architecture firm was tasked with designing a building with a sloping roof. The roof was to be angled at 30 degrees, and the height of the roof at the peak was to be 10 meters. The building was also to have a glass wall facing south, and the angle of the glass wall was to be 60 degrees with respect to the horizontal.
Solution: To design the building, the architecture firm needed to use trigonometric functions to calculate various angles and distances.
Firstly, the firm used the sine function to calculate the height of the building at the point where the roof met the wall. They knew that the angle of the roof was 30 degrees, and the height at the peak was 10 meters. By using the formula sin(30) = opposite/hypotenuse, they calculated that the height at the point where the roof met the wall was 5 meters.
Secondly, the architecture firm used the tangent function to calculate the length of the roof. They knew that the angle of the roof was 30 degrees, and they needed to calculate the length of the roof from the peak to the point where it met the wall. By using the formula tan(30) = opposite/adjacent, they calculated that the length of the roof was approximately 8.66 meters.
Finally, the firm used the cosine function to calculate the height of the glass wall. They knew that the angle of the glass wall was 60 degrees with respect to the horizontal, and they needed to calculate the height of the glass wall. By using the formula cos(60) = adjacent/hypotenuse, they calculated that the height of the glass wall was approximately 5 meters.
By using trigonometric functions, the architecture firm was able to accurately design a building with a sloping roof and a glass wall facing south.
Conclusion: Trigonometric functions are essential tools in architecture, allowing architects to accurately calculate angles and distances in the design of buildings and structures. In this case study, the architecture firm used trigonometric functions to calculate the height and length of a sloping roof and the height of a glass wall, demonstrating the practical application of these functions in real-world situations.
White paper on Trigonometric functions
Introduction:
Trigonometric functions are mathematical functions that relate angles to the sides of a right triangle. These functions have numerous applications in mathematics, science, and engineering, making them an essential tool for many fields.
In this white paper, we will explore the properties and applications of trigonometric functions, including the primary trigonometric functions, their inverses, and other related functions. We will also discuss their applications in various fields, including astronomy, physics, engineering, and architecture.
Primary Trigonometric Functions:
The primary trigonometric functions are the sine, cosine, and tangent functions, which are commonly denoted as sin, cos, and tan, respectively. These functions are defined as ratios of the sides of a right triangle.
The sine function (sin) relates the ratio of the length of the side opposite to an angle and the length of the hypotenuse of a right triangle. The cosine function (cos) relates the ratio of the length of the adjacent side and the hypotenuse of a right triangle. The tangent function (tan) relates the ratio of the length of the opposite side and the adjacent side of a right triangle.
Other Trigonometric Functions:
In addition to the primary trigonometric functions, there are several other related functions, including the cosecant (csc), secant (sec), and cotangent (cot), which are reciprocals of the sine, cosine, and tangent functions, respectively.
Inverse Trigonometric Functions:
The inverse trigonometric functions are used to find the angle of a right triangle given the ratio of its sides. The inverse trigonometric functions include arcsin, arccos, and arctan, which are denoted as sin⁻¹, cos⁻¹, and tan⁻¹, respectively.
Applications of Trigonometric Functions:
Trigonometric functions have many applications in various fields. In astronomy, trigonometric functions are used to calculate the positions of celestial objects and to determine distances between celestial bodies. In physics, trigonometric functions are used to describe wave motion and oscillations.
In engineering, trigonometric functions are used to design and analyze structures, such as bridges, buildings, and towers. In architecture, trigonometric functions are used to calculate angles and distances when designing buildings and structures.
Conclusion:
Trigonometric functions are fundamental mathematical functions that have numerous applications in various fields, including mathematics, science, and engineering. The primary trigonometric functions, their inverses, and related functions are essential tools for solving problems involving angles and distances. By understanding the properties and applications of trigonometric functions, we can better appreciate their significance in the world around us.