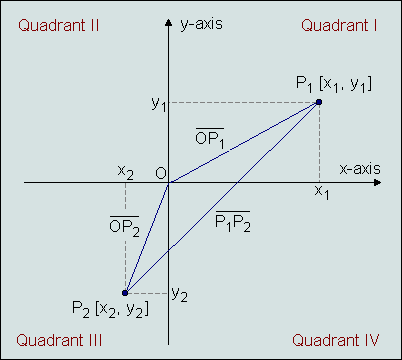
Analytical geometry in two dimensions is the branch of mathematics that deals with the study of geometric shapes using algebraic methods. The Cartesian coordinate system is the most common system used in analytical geometry, and it allows us to represent points, lines, curves, and other geometric figures using numerical values.
In the Cartesian coordinate system, two perpendicular number lines intersect at a point called the origin. The horizontal line is called the x-axis, and the vertical line is called the y-axis. Each point in the plane can be represented by a pair of numbers (x, y), where x is the horizontal coordinate and y is the vertical coordinate.
The distance between two points (x1, y1) and (x2, y2) in the Cartesian coordinate system can be found using the distance formula:
d = sqrt((x2 – x1)^2 + (y2 – y1)^2)
A line in the Cartesian coordinate system can be represented using its slope-intercept form:
y = mx + b
where m is the slope of the line, and b is the y-intercept (the point where the line intersects the y-axis). The slope of a line is given by the formula:
m = (y2 – y1) / (x2 – x1)
where (x1, y1) and (x2, y2) are any two points on the line.
To find the equation of a line passing through two given points, we can first find the slope of the line using the formula above and then use the point-slope form of the equation:
y – y1 = m(x – x1)
where (x1, y1) is one of the given points.
The midpoint of a line segment with endpoints (x1, y1) and (x2, y2) can be found using the midpoint formula:
((x1 + x2) / 2, (y1 + y2) / 2)
Finally, we can also use the Cartesian coordinate system to represent and analyze conic sections, such as circles, ellipses, parabolas, and hyperbolas, using algebraic equations.
What is Required Two dimensions: Cartesian coordinates
To understand and work with analytical geometry in two dimensions using Cartesian coordinates, you will need to have a good understanding of algebraic equations, especially linear and quadratic equations. You will also need to be familiar with the properties of points, lines, and curves in the Cartesian coordinate system.
Some specific concepts and skills you will need to know include:
- The Cartesian coordinate system and how to plot points in it.
- The distance formula and how to use it to find the distance between two points.
- The slope of a line and how to find it, as well as the different forms of a linear equation (slope-intercept form, point-slope form, and standard form).
- How to find the equation of a line given two points, or given its slope and y-intercept.
- How to find the midpoint of a line segment.
- The properties of circles, including their equation and how to find their center and radius.
- The equation and properties of other conic sections, such as ellipses, parabolas, and hyperbolas.
- How to use algebraic methods to analyze and manipulate geometric figures in the Cartesian plane.
- Basic trigonometry, including the relationships between sine, cosine, and tangent, and how to use them to find angles and distances in the Cartesian plane.
Having a solid foundation in these concepts and skills will allow you to work with and solve problems involving geometric figures in the Cartesian plane, and will also help you understand more advanced topics in geometry and mathematics.
Who is Required Two dimensions: Cartesian coordinates
The knowledge of analytical geometry in two dimensions using Cartesian coordinates is essential for anyone studying or working in fields such as mathematics, physics, engineering, computer science, and other related disciplines.
In mathematics, analytical geometry provides a foundation for the study of more advanced topics, such as calculus and linear algebra. It is also used extensively in physics, where it is applied to the analysis of motion, force, and energy in two-dimensional systems.
In engineering and computer science, analytical geometry is used in the design and analysis of structures, circuits, and systems, as well as in computer graphics and image processing.
Other fields where analytical geometry in two dimensions is important include architecture, geography, and surveying, where it is used to represent and analyze physical spaces and their features.
In summary, anyone who works with or studies geometric shapes, physical systems, or mathematical models will benefit from a solid understanding of analytical geometry in two dimensions using Cartesian coordinates.
When is Required Two dimensions: Cartesian coordinates
The knowledge of analytical geometry in two dimensions using Cartesian coordinates is required in various situations, including:
- Solving mathematical problems involving geometric shapes, such as finding the equation of a line, the distance between two points, or the coordinates of a midpoint.
- Analyzing physical systems in two dimensions, such as the motion of a projectile, the forces acting on a structure, or the behavior of a circuit.
- Designing and analyzing computer graphics and image processing algorithms, which often involve geometric transformations and manipulations in two dimensions.
- Working with geographic information systems (GIS) and spatial analysis, which rely on the representation and analysis of geographic data using Cartesian coordinates.
- Performing surveying and mapping tasks, where accurate measurements and calculations of distances and angles in two-dimensional space are essential.
- Conducting research in various scientific fields, such as physics, engineering, computer science, and mathematics, where analytical geometry is a foundational concept.
Overall, analytical geometry in two dimensions using Cartesian coordinates is required whenever the representation, analysis, or manipulation of geometric shapes, physical systems, or mathematical models in two-dimensional space is needed.
Where is Required Two dimensions: Cartesian coordinates
The knowledge of analytical geometry in two dimensions using Cartesian coordinates is used in various fields and applications, including:
- Mathematics: Analytical geometry is a foundational concept in mathematics, and it is used to solve problems in algebra, calculus, and other advanced mathematical topics.
- Physics: Analytical geometry is used to represent and analyze physical systems, such as the motion of objects in two dimensions, forces acting on a structure, or the behavior of a circuit.
- Engineering: Engineers use analytical geometry to design and analyze structures, circuits, and systems in two dimensions.
- Computer science: Analytical geometry is used in computer graphics, image processing, and other areas where the manipulation of geometric objects is required.
- Architecture: Architects use analytical geometry to design and analyze buildings, including floor plans and elevations.
- Geography and GIS: Analytical geometry is used in geographic information systems (GIS) and spatial analysis to represent and analyze geographic data.
- Surveying and mapping: Surveyors and cartographers use analytical geometry to measure and calculate distances, angles, and areas in two-dimensional space.
Overall, analytical geometry in two dimensions using Cartesian coordinates is used in various fields and applications where the representation, analysis, or manipulation of geometric shapes, physical systems, or mathematical models in two-dimensional space is needed.
How is Required Two dimensions: Cartesian coordinates
Analytical geometry in two dimensions using Cartesian coordinates is approached by using algebraic techniques to represent geometric figures in a two-dimensional plane. This involves assigning coordinates to points on the plane, and using algebraic equations to describe lines, curves, and other shapes.
The Cartesian coordinate system is used to assign coordinates to points on the plane. In this system, two perpendicular lines called the x-axis and y-axis intersect at the origin (0,0), and each point on the plane is assigned a unique pair of numbers (x,y), where x is the horizontal coordinate and y is the vertical coordinate.
Once points are assigned coordinates, algebraic equations can be used to represent lines, curves, and other shapes on the plane. For example, the equation of a straight line in the plane can be represented in various forms, including slope-intercept form (y = mx + b), point-slope form ((y – y1) = m(x – x1)), and standard form (Ax + By = C), where m is the slope of the line, b is the y-intercept, (x1, y1) is a point on the line, and A, B, and C are constants.
Other geometric shapes, such as circles, ellipses, parabolas, and hyperbolas, can also be represented using algebraic equations, often in the form of quadratic equations.
To work with analytical geometry in two dimensions using Cartesian coordinates, it is necessary to have a good understanding of algebraic equations, as well as the properties of points, lines, curves, and other shapes in the plane. With this knowledge, it is possible to analyze and manipulate geometric figures in a wide range of applications, from mathematics and physics to engineering and computer science.
Case Study on Two dimensions: Cartesian coordinates
One example of a case study that involves the use of analytical geometry in two dimensions using Cartesian coordinates is the design of a roller coaster track.
The design of a roller coaster track requires careful consideration of the physics involved, as well as the safety of the riders. One important aspect of the design is the shape of the track, which can be represented using analytical geometry in two dimensions using Cartesian coordinates.
To design a roller coaster track, the first step is to determine the shape of the initial drop. This is typically a steep descent that sets the momentum for the rest of the ride. The shape of the drop can be represented using a curve, such as a parabola, that has a specific slope and curvature.
Next, the track must be designed to provide a series of thrilling twists and turns, while ensuring that the riders remain safe and secure. This requires careful consideration of the track’s banking, or the angle at which it tilts in relation to the ground.
The banking of the track is critical for maintaining the safety of the riders and ensuring that they do not experience excessive g-forces during the ride. Analytical geometry can be used to calculate the optimal banking angle for each section of the track, based on factors such as the radius of curvature, the speed of the ride, and the desired g-forces experienced by the riders.
Finally, the design of the roller coaster track must be optimized for aesthetics and visual appeal. This can be achieved by incorporating loops, corkscrews, and other elements that add excitement and thrill to the ride.
Overall, the design of a roller coaster track is a complex process that requires a deep understanding of physics, engineering, and geometry. Analytical geometry in two dimensions using Cartesian coordinates plays a critical role in this process, as it provides a powerful tool for representing, analyzing, and manipulating the shapes and curves of the track.
White paper on Two dimensions: Cartesian coordinates
Introduction
Analytical geometry in two dimensions using Cartesian coordinates is a branch of mathematics that allows us to describe and analyze geometric figures using algebraic equations. This white paper will provide an overview of analytical geometry in two dimensions using Cartesian coordinates, including the history of the subject, its applications, and its key concepts.
History
The roots of analytical geometry can be traced back to the ancient Greeks, who were interested in studying geometric shapes and figures. However, the modern form of analytical geometry was developed in the 17th century by the French mathematician René Descartes. Descartes realized that geometric shapes could be represented using algebraic equations, and he introduced the concept of the Cartesian coordinate system, which allowed points on a plane to be represented using numerical coordinates.
Key Concepts
The Cartesian coordinate system is a fundamental concept in analytical geometry in two dimensions using Cartesian coordinates. It consists of two perpendicular axes, the x-axis and y-axis, which intersect at the origin. Each point on the plane is assigned a unique pair of numbers (x, y), where x represents the horizontal distance from the y-axis and y represents the vertical distance from the x-axis.
Using the Cartesian coordinate system, it is possible to represent lines, curves, and other geometric figures using algebraic equations. For example, a straight line in the plane can be represented using the equation y = mx + b, where m is the slope of the line and b is the y-intercept. Similarly, a circle can be represented using the equation (x – a)² + (y – b)² = r², where (a, b) represents the center of the circle and r represents the radius.
Applications
Analytical geometry in two dimensions using Cartesian coordinates has a wide range of applications in various fields, including mathematics, physics, engineering, computer science, architecture, geography, and surveying. In mathematics, analytical geometry is used to solve problems in algebra, calculus, and other advanced mathematical topics. In physics, it is used to represent and analyze physical systems, such as the motion of objects in two dimensions or the behavior of a circuit. In engineering, it is used to design and analyze structures, circuits, and systems in two dimensions. In computer science, it is used in computer graphics, image processing, and other areas where the manipulation of geometric objects is required. In architecture, analytical geometry is used to design and analyze buildings, including floor plans and elevations. In geography and GIS, analytical geometry is used in geographic information systems and spatial analysis to represent and analyze geographic data. In surveying and mapping, analytical geometry is used to measure and calculate distances, angles, and areas in two-dimensional space.
Conclusion
Analytical geometry in two dimensions using Cartesian coordinates is a powerful tool for representing, analyzing, and manipulating geometric figures using algebraic equations. Its applications span a wide range of fields, from mathematics and physics to engineering and computer science. The Cartesian coordinate system and its key concepts, such as lines, curves, and other shapes, provide a fundamental framework for understanding and solving problems in analytical geometry.