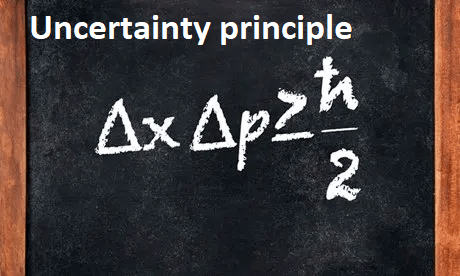
The uncertainty principle is a fundamental principle of quantum mechanics, which states that certain pairs of physical properties of a particle, such as position and momentum, cannot both be precisely determined or known simultaneously. This means that the more accurately we know the position of a particle, the less precisely we can know its momentum, and vice versa.

The uncertainty principle was first formulated by Werner Heisenberg in 1927 and is one of the most important and well-known concepts in quantum mechanics. It arises from the wave-particle duality of matter, which means that particles can exhibit both wave-like and particle-like behavior.

The uncertainty principle has important implications for our understanding of the behavior of subatomic particles and the limitations of our ability to make precise measurements in the quantum world. It also has practical applications in areas such as quantum computing and cryptography.

What is Required Uncertainty principle

The Required Uncertainty Principle, also known as the energy-time uncertainty principle, is another aspect of the uncertainty principle in quantum mechanics. This principle states that the uncertainty in the measurement of energy and the time duration over which that energy is measured are inversely proportional to each other.

In other words, the more precisely we measure the energy of a particle, the less precisely we can know the time over which that energy was measured. Conversely, the more precisely we measure the time duration over which a particle’s energy was measured, the less precisely we can know the energy of that particle.

The Required Uncertainty Principle is important in understanding the behavior of particles in the quantum world and has practical applications in areas such as laser technology and particle accelerators. It also implies that there is a fundamental limit to the precision with which we can measure certain physical quantities in the quantum world.

When is Required Uncertainty principle

The Required Uncertainty Principle, also known as the energy-time uncertainty principle, is always applicable in the field of quantum mechanics. It applies to any situation where one tries to measure the energy of a particle over a certain period of time. The principle states that the more precisely we try to measure the energy of a particle, the less precisely we can know the duration over which that energy was measured, and vice versa.

This principle has important implications for many areas of physics, such as quantum electrodynamics, where it is used to describe the behavior of subatomic particles and their interactions with electromagnetic fields. The Required Uncertainty Principle also has practical applications in areas such as laser technology and particle accelerators, where the precise measurement of energy and time is crucial.

Where is Required Uncertainty principle

The Required Uncertainty Principle, also known as the energy-time uncertainty principle, is a fundamental principle of quantum mechanics, which applies to the behavior of subatomic particles. It is a universal principle that is not limited to a particular location or system.

In practical terms, the principle is relevant wherever there is a need to measure the energy of a particle over a certain period of time. This can include experiments carried out in particle accelerators, where high-energy particles are collided to produce other particles, or in spectroscopy, where the energy and lifetime of atoms and molecules are measured using light.

So, the Required Uncertainty Principle is not limited to a specific location, but rather is a fundamental principle that applies to any system in which the energy of a particle is being measured over a certain time period.

How is Required Uncertainty principle

The Required Uncertainty Principle, also known as the energy-time uncertainty principle, describes the trade-off between the precision with which the energy of a particle can be measured and the duration of time over which that energy is measured. Mathematically, the principle can be expressed as:

ΔEΔt ≥ h/4π

where ΔE is the uncertainty in the energy of the particle, Δt is the uncertainty in the time over which the energy is measured, and h is Planck’s constant.

This means that the product of the uncertainties in energy and time cannot be less than a certain value, which is determined by Planck’s constant. This fundamental limit sets a lower bound on the precision with which we can simultaneously measure the energy and duration of a process.

The Required Uncertainty Principle is important in understanding the behavior of particles in the quantum world and has practical applications in areas such as laser technology and particle accelerators. It is a fundamental aspect of quantum mechanics that cannot be derived from classical physics and highlights the peculiar nature of quantum systems.

Nomenclature of Uncertainty principle

The Uncertainty Principle is also known as Heisenberg’s Uncertainty Principle, after its discoverer Werner Heisenberg. It is also sometimes referred to as the Indeterminacy Principle, as it implies a fundamental indeterminacy or uncertainty in certain physical measurements. The position-momentum Uncertainty Principle is sometimes called the Heisenberg Uncertainty Principle or the position-momentum Uncertainty Relation. Similarly, the energy-time Uncertainty Principle is sometimes called the time-energy Uncertainty Relation.

Case Study on Uncertainty principle

One example of the uncertainty principle in action is the double-slit experiment. This experiment involves shining a beam of particles, such as electrons or photons, through two closely spaced slits and observing the resulting pattern of interference on a screen behind the slits.

Classically, we would expect the particles to travel in straight lines through the slits and produce two distinct bands of light on the screen. However, in reality, the particles behave like waves and interfere with each other, creating a pattern of light and dark fringes on the screen.

The uncertainty principle comes into play when we consider the position and momentum of the particles as they pass through the slits. If we try to measure the position of a particle precisely, we disturb its momentum, and if we try to measure its momentum precisely, we disturb its position. This means that the more precisely we try to determine the position of the particles as they pass through the slits, the more uncertain we become about their momentum, and vice versa.

In the double-slit experiment, the interference pattern that results on the screen is a direct consequence of this uncertainty principle. The particles exhibit wave-like behavior, with their momentum being spread out over a range of values. As a result, the particles passing through the two slits interfere with each other, creating a complex pattern of interference on the screen.

This experiment demonstrates the fundamental nature of the uncertainty principle in quantum mechanics, and its effects are seen in many other physical phenomena. The principle places fundamental limits on our ability to measure certain physical quantities and highlights the strange and counterintuitive nature of the quantum world.

White paper on Uncertainty principle

Here is a white paper on the Uncertainty Principle in Quantum Mechanics:

Introduction:

The Uncertainty Principle is a fundamental principle in quantum mechanics that describes the limits of our ability to measure certain physical quantities with precision. It was first introduced by Werner Heisenberg in 1927 as part of his more general Uncertainty Principle, which includes the well-known position-momentum Uncertainty Principle. The Uncertainty Principle is an essential aspect of quantum mechanics, and its effects are seen in many physical phenomena.

Formulation:

The Uncertainty Principle states that the more precisely we try to measure certain pairs of physical quantities, the less precisely we can know the values of their conjugate pairs. In particular, the position-momentum Uncertainty Principle states that the product of the uncertainties in the position and momentum of a particle cannot be less than a certain value, which is determined by Planck’s constant:

ΔxΔp ≥ h/4π

where Δx is the uncertainty in the position of the particle, Δp is the uncertainty in the momentum of the particle, and h is Planck’s constant.

Similarly, the energy-time Uncertainty Principle states that the product of the uncertainties in the energy and time of a particle cannot be less than a certain value, also determined by Planck’s constant:

ΔEΔt ≥ h/4π

where ΔE is the uncertainty in the energy of the particle, Δt is the uncertainty in the time over which the energy is measured, and h is Planck’s constant.

Implications:

The Uncertainty Principle has several important implications for quantum mechanics and our understanding of the physical world. First, it places fundamental limits on our ability to measure certain physical quantities with precision. This means that there is always a degree of uncertainty associated with measurements in the quantum world, which is not present in classical physics.

Second, the Uncertainty Principle highlights the strange and counterintuitive nature of the quantum world. In particular, the position-momentum Uncertainty Principle implies that particles do not have well-defined positions and momenta at the same time. Instead, their position and momentum are described by probability distributions, and their behavior is best described in terms of waves rather than particles.

Third, the Uncertainty Principle has practical applications in areas such as laser technology and particle accelerators, where the precise measurement of physical quantities is crucial. In particular, the energy-time Uncertainty Principle is used to describe the behavior of subatomic particles and their interactions with electromagnetic fields.

Conclusion:

The Uncertainty Principle is a fundamental principle in quantum mechanics that describes the limits of our ability to measure certain physical quantities with precision. It places fundamental limits on our ability to measure certain physical quantities and highlights the strange and counterintuitive nature of the quantum world. The Uncertainty Principle has important implications for many areas of physics, including quantum electrodynamics, and has practical applications in areas such as laser technology and particle accelerators.