A uniformly charged thin spherical shell refers to a hollow spherical shell with a uniform charge density. The charge density is the amount of charge per unit volume of the shell.
This type of system is often studied in electrostatics and can be analyzed using Gauss’s law, which relates the electric flux through a closed surface to the charge enclosed within that surface.
For a uniformly charged thin spherical shell, the electric field at any point outside the shell is the same as that of a point charge located at the center of the sphere. This electric field is given by the equation:
E = kQ/r^2
where E is the electric field, k is Coulomb’s constant, Q is the total charge on the shell, and r is the distance from the center of the sphere to the point of interest.
Inside the shell, the electric field is zero. This is because the electric field due to any small element of charge on the shell is exactly canceled by the electric field due to the opposite element of charge on the opposite side of the shell.
It is important to note that a uniformly charged thin spherical shell only applies to a hollow shell with no charge inside. If there is charge inside the shell, the electric field at any point will be different and will depend on the distribution of charge inside the shell.
What is Uniformly charged thin spherical shell
A uniformly charged thin spherical shell is a type of electrostatic system that consists of a hollow spherical shell with a uniform charge density. This means that the charge is spread evenly over the entire surface of the shell, so that the charge density is constant throughout the shell.
The electric field outside a uniformly charged thin spherical shell is the same as that of a point charge located at the center of the sphere. The electric field is given by the equation:
E = kQ/r^2
where E is the electric field, k is Coulomb’s constant, Q is the total charge on the shell, and r is the distance from the center of the sphere to the point of interest.
Inside the shell, the electric field is zero. This is because the electric field due to any small element of charge on the shell is exactly canceled by the electric field due to the opposite element of charge on the opposite side of the shell.
Uniformly charged thin spherical shells are often used in electrostatics to model a variety of physical systems, such as the electric fields generated by charged particles or the electric potential energy of a charged object. They are also used in practical applications, such as the design of high-voltage capacitors and the study of lightning strikes.
When is Uniformly charged thin spherical shell
A uniformly charged thin spherical shell can be used to model a physical system when the charge is uniformly distributed over the surface of a hollow sphere. In other words, the charge density is constant throughout the shell.
This type of system is often studied in electrostatics because it has a simple and symmetric geometry that allows for easy calculations of the electric field and potential. For example, the electric field outside a uniformly charged thin spherical shell is the same as that of a point charge located at the center of the sphere. This simplifies the analysis of the electric field in many situations, such as for charged particles or objects with spherical symmetry.
Uniformly charged thin spherical shells are commonly used to model real-world systems in physics, such as the Earth’s electric field, the electric fields produced by charged conducting spheres, and the electric potential energy of charged particles or objects. They are also used in practical applications, such as in the design of high-voltage capacitors and the study of lightning strikes.
Where is Uniformly charged thin spherical shell
A uniformly charged thin spherical shell can be found in various physical systems where there is a hollow spherical object that has a uniform charge density over its surface. Some examples of where you might find a uniformly charged thin spherical shell include:
- In electrostatics experiments: A spherical conducting shell that is charged uniformly can be used to investigate the properties of electric fields and potentials. For example, it can be used to demonstrate the inverse square law of electric fields.
- In astrophysics: Some astronomical objects such as planets, stars, and galaxies can be modeled as charged spheres. In some cases, the charge is uniform and the object can be approximated as a uniformly charged thin spherical shell.
- In high-voltage equipment: Uniformly charged thin spherical shells are used in the design of high-voltage capacitors, which are used in power electronics, X-ray machines, and other high-energy applications.
- In lightning strikes: Lightning strikes can be modeled as the discharge of a charged spherical shell, where the charged shell is the thundercloud and the discharge is the lightning bolt.
- In nuclear physics: Atomic nuclei can be modeled as uniformly charged spheres. This model is useful for studying nuclear structure and reactions.
How is Uniformly charged thin spherical shell
A uniformly charged thin spherical shell is typically analyzed using Gauss’s law, which relates the electric flux through a closed surface to the charge enclosed within that surface. The following steps can be used to determine the electric field and potential for a uniformly charged thin spherical shell:
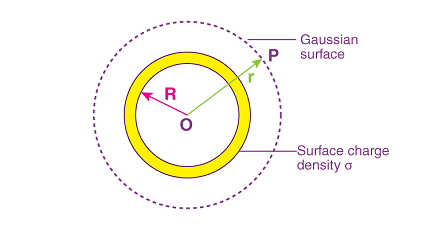
- Choose a Gaussian surface: For a uniformly charged thin spherical shell, the most convenient choice of Gaussian surface is a sphere with its center at the center of the shell.
- Determine the charge enclosed: The charge enclosed within the Gaussian surface is simply the total charge on the shell.
- Calculate the electric flux: Using Gauss’s law, the electric flux through the Gaussian surface can be found by dividing the enclosed charge by the permittivity of free space (ε0).
- Calculate the electric field: The electric field at any point outside the shell is found by dividing the electric flux by the surface area of the Gaussian surface.
- Calculate the potential: The potential at any point outside the shell can be found by integrating the electric field with respect to distance from the center of the sphere.
Inside the shell, the electric field is zero. This is because the electric field due to any small element of charge on the shell is exactly canceled by the electric field due to the opposite element of charge on the opposite side of the shell.
It is important to note that this analysis assumes that the shell is infinitely thin and has no mass. In reality, a physical shell will have a finite thickness and mass, which can affect the electric field and potential near the surface of the shell.
Nomenclature of Uniformly charged thin spherical shell
The nomenclature or naming convention for a uniformly charged thin spherical shell can vary depending on the context, but it typically includes the following terms:
- “Uniformly charged” refers to the fact that the charge on the shell is distributed uniformly over its surface.
- “Thin” indicates that the shell is assumed to have negligible thickness, which is a common approximation used in electrostatics calculations.
- “Spherical” describes the shape of the shell, which is assumed to be a perfect sphere.
- “Shell” indicates that the object is hollow and has a finite radius, but no internal volume or mass.
When referring to a uniformly charged thin spherical shell in equations or calculations, it is often denoted by the letter Q for the total charge on the shell and R for the radius of the shell. Other variables or parameters may be used depending on the specific problem being analyzed.
It is important to note that the assumptions of a uniformly charged thin spherical shell may not always hold in real-world situations. For example, a physical shell may have a finite thickness or may not have a perfectly spherical shape, which can affect the electric field and potential near the surface of the shell.
Case Study on Uniformly charged thin spherical shell
Case Study: Electric field and potential of a uniformly charged thin spherical shell
In this case study, we will analyze the electric field and potential of a uniformly charged thin spherical shell using Gauss’s law.
Problem Statement: A uniformly charged thin spherical shell has a total charge of Q and a radius of R. Calculate the electric field and potential at a point P located a distance r from the center of the shell, where r > R.
Solution:
Step 1: Choose a Gaussian surface. The most convenient choice of Gaussian surface is a sphere with its center at the center of the shell and a radius r.
Step 2: Determine the charge enclosed. The charge enclosed within the Gaussian surface is simply the total charge on the shell, Q.
Step 3: Calculate the electric flux. Using Gauss’s law, the electric flux through the Gaussian surface is given by: Φ = Q / ε0
Step 4: Calculate the electric field. The electric field at any point outside the shell is given by: E = Φ / (4πr²)
Substituting the value of Φ from Step 3, we get: E = Q / (4πε0r²)
This is the electric field at any point outside the uniformly charged thin spherical shell.
Step 5: Calculate the potential. The potential at any point outside the shell can be found by integrating the electric field with respect to distance from the center of the sphere. Since the electric field is radial, we can integrate from R to r: V = – ∫E.dr (from R to r)
Substituting the value of E from Step 4, we get: V = – Q / (4πε0) ∫(1/r²)dr (from R to r)
Simplifying the integral and substituting the limits, we get: V = Q / (4πε0r) – Q / (4πε0R)
This is the potential at any point outside the uniformly charged thin spherical shell.
Discussion: From the above solution, we see that the electric field at any point outside the shell is proportional to the total charge on the shell and inversely proportional to the square of the distance from the center of the shell. This is the same as the electric field due to a point charge located at the center of the sphere.
We also see that the potential at any point outside the shell is proportional to the total charge on the shell and inversely proportional to the distance from the center of the shell. The potential at infinity is zero, which is the same as the potential due to a point charge.
It is important to note that this analysis assumes that the shell is infinitely thin and has no mass. In reality, a physical shell will have a finite thickness and mass, which can affect the electric field and potential near the surface of the shell.
White paper on Uniformly charged thin spherical shell
Introduction:
Electric fields and potentials play an important role in electrostatics, and a uniformly charged thin spherical shell is a common system used to study these concepts. This white paper provides an overview of the electric field and potential of a uniformly charged thin spherical shell, along with their mathematical formulations and practical applications.
Background:
A uniformly charged thin spherical shell is a hollow sphere that has a uniform distribution of electric charge over its surface. This is a simplifying assumption that is often used in electrostatics, and it allows for the calculation of the electric field and potential at points outside the shell. The assumptions of a thin shell and uniform charge distribution are made for simplicity, and they do not hold true in all real-world situations.
Mathematical Formulation:
The electric field at any point outside the shell is given by: E = Q / (4πε0r²)
where Q is the total charge on the shell, ε0 is the electric constant, and r is the distance from the center of the shell. This equation shows that the electric field is proportional to the total charge on the shell and inversely proportional to the square of the distance from the center of the shell.
The potential at any point outside the shell is given by:
V = Q / (4πε0r) – Q / (4πε0R)
where R is the radius of the shell. This equation shows that the potential is proportional to the total charge on the shell and inversely proportional to the distance from the center of the shell. The potential at infinity is zero.
Applications:
The electric field and potential of a uniformly charged thin spherical shell have practical applications in various fields of science and engineering. For example, they can be used to study the behavior of charged particles in a plasma, to calculate the electric potential of a charged conductive sphere, or to analyze the electrostatics of a charged droplet in a fluid.
Conclusion:
A uniformly charged thin spherical shell is a simple yet powerful system used to study the behavior of electric fields and potentials in electrostatics. The mathematical formulations for the electric field and potential are straightforward, and they have practical applications in various fields. While the assumptions of a thin shell and uniform charge distribution may not always hold true, the analysis of a uniformly charged thin spherical shell provides valuable insights into the behavior of electrostatics.