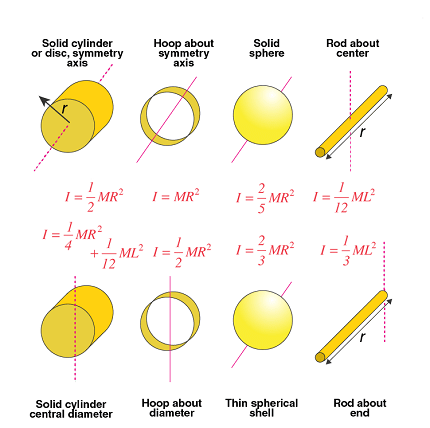
Moment of Inertia is a measure of an object’s resistance to changes in its rotational motion. It is defined as the sum of the products of the mass of each particle in the object, and the square of its distance from the axis of rotation.

The moment of inertia of an object depends on its shape and the distribution of mass within the object. For example, a long thin rod will have a lower moment of inertia than a solid cylinder with the same mass and radius, because more of the mass in the rod is concentrated near the axis of rotation.

The formula for calculating the moment of inertia of a rigid body is:

I = ∫ r^2 dm

where I is the moment of inertia, r is the distance of a particle from the axis of rotation, and dm is the mass of a small element of the object. The integral is taken over the entire mass of the object.

The moment of inertia has units of kg⋅m² in the SI system of units. It plays an important role in physics, engineering, and mechanics, and is used to analyze the rotational motion of objects such as wheels, gears, and turbines.

What is Required Mechanics Moment of Inertia

Required Mechanics Moment of Inertia is a term that is often used in engineering and mechanics. It refers to the moment of inertia that is needed to achieve a certain level of performance or functionality in a mechanical system.

For example, in a rotating machine such as a motor or generator, the required moment of inertia may be specified in order to ensure that the machine can operate smoothly and maintain a constant speed under varying loads. In this case, a higher moment of inertia may be required to provide the necessary stability and prevent the machine from stalling or slowing down.

Similarly, in a robotic arm or other mechanical system that requires precise control over its motion, the required moment of inertia may be specified to ensure that the system can respond quickly and accurately to commands. In this case, a lower moment of inertia may be desirable to reduce the amount of energy required to move the system and improve its responsiveness.

The required moment of inertia depends on the specific requirements of the system and can be calculated using the formulas and principles of mechanics and engineering.

When is Required Mechanics Moment of Inertia

The Required Mechanics Moment of Inertia is used in a variety of applications in engineering and mechanics. Some examples of when it may be used include:

1. Rotating machinery: In rotating machinery such as motors, generators, or turbines, the required moment of inertia is important for ensuring stable operation and maintaining a constant speed. A higher moment of inertia may be required to provide the necessary stability and prevent the machine from stalling or slowing down.
2. Robotics: In robotic systems such as robotic arms or drones, the required moment of inertia is important for achieving precise control over motion. A lower moment of inertia may be desirable to reduce the amount of energy required to move the system and improve its responsiveness.
3. Aerospace: In aerospace applications such as satellites or spacecraft, the required moment of inertia is important for maintaining stability and control over the vehicle’s motion. A higher moment of inertia may be required to prevent unwanted movements or disturbances from affecting the vehicle’s trajectory.
4. Sports equipment: In sports equipment such as golf clubs or tennis rackets, the required moment of inertia is important for achieving optimal performance. For example, a golf club with a higher moment of inertia may be more forgiving of off-center hits, while a tennis racket with a lower moment of inertia may be more maneuverable and easier to swing.

Overall, the Required Mechanics Moment of Inertia is a key parameter that is used in many different applications to ensure optimal performance and functionality of mechanical systems.

Where is Required Mechanics Moment of Inertia

The Required Mechanics Moment of Inertia is a concept that is used in various fields of engineering and mechanics. It is used to describe the amount of resistance a body has to rotational motion and is an important parameter in the design and analysis of mechanical systems.

The Required Mechanics Moment of Inertia can be found in a variety of applications such as:

1. Rotating machinery: In motors, generators, and other rotating equipment, the Required Mechanics Moment of Inertia is used to ensure stable operation and maintain a constant speed.
2. Robotics: In robotic systems, the Required Mechanics Moment of Inertia is used to achieve precise control over motion.
3. Aerospace: In aerospace applications, the Required Mechanics Moment of Inertia is used to maintain stability and control over the vehicle’s motion.
4. Sports equipment: In sports equipment such as golf clubs, tennis rackets, and baseball bats, the Required Mechanics Moment of Inertia is used to achieve optimal performance.

Overall, the Required Mechanics Moment of Inertia is a fundamental concept in mechanics and is used in a wide range of applications across many different fields of engineering.

How is Required Mechanics Moment of Inertia

The Required Mechanics Moment of Inertia is a measure of an object’s resistance to changes in its rotational motion, and it is determined by the object’s mass distribution and geometry. The calculation of the Required Mechanics Moment of Inertia involves integrating the product of the mass of each element of the object and its distance from the axis of rotation, squared.

The general formula for calculating the Required Mechanics Moment of Inertia of a rigid body is:

I = ∫ r^2 dm

where I is the Required Mechanics Moment of Inertia, r is the distance of a particle from the axis of rotation, and dm is the mass of a small element of the object. The integral is taken over the entire mass of the object.

The Required Mechanics Moment of Inertia can be calculated for simple geometric shapes such as cylinders, spheres, and cones using standard formulas. For more complex shapes, numerical methods such as finite element analysis may be used.

In engineering and mechanics, the Required Mechanics Moment of Inertia is an important parameter that is used to determine the stability, response, and performance of mechanical systems. It is used in the design and analysis of various machines, from simple rotating machinery to advanced aerospace vehicles and robotic systems.

Structures of Mechanics Moment of Inertia

The moment of inertia of a structure is a physical property that describes the resistance of the structure to rotational motion around an axis. It is an important parameter in engineering and mechanics, as it affects the stability, response, and performance of mechanical systems.

There are different types of structures that have their own moments of inertia, including:

1. Beams: A beam is a structural element that supports loads by resisting bending. The moment of inertia of a beam depends on its cross-sectional shape and size. For example, a rectangular beam has a moment of inertia that is proportional to its width and the cube of its height.
2. Cylinders: A cylinder is a three-dimensional object with a circular cross-section. The moment of inertia of a cylinder depends on its radius and length. The moment of inertia of a solid cylinder is greater than that of a hollow cylinder of the same mass and dimensions.
3. Spheres: A sphere is a three-dimensional object with a spherical shape. The moment of inertia of a sphere depends on its radius. A solid sphere has a higher moment of inertia than a hollow sphere of the same mass and dimensions.
4. Plates: A plate is a flat, two-dimensional object with a constant thickness. The moment of inertia of a plate depends on its geometry, such as its shape and size. For example, a rectangular plate has a moment of inertia that is proportional to its width, the cube of its height, and the thickness of the plate.
5. Complex structures: For more complex structures, the moment of inertia can be calculated by dividing the structure into smaller, simpler parts, and using the principle of superposition to add up the moments of inertia of each part.

In summary, the moment of inertia of a structure depends on its geometry, mass distribution, and orientation with respect to the axis of rotation. It is an important parameter in engineering and mechanics that is used to analyze the stability and performance of mechanical systems.

Case Study on Mechanics Moment of Inertia

One example of the use of mechanics moment of inertia is in the design of a rotating shaft. A rotating shaft is a common component of many machines, such as engines, generators, and turbines. The moment of inertia of the shaft affects its ability to store and transfer energy, its resistance to bending and torsion, and its overall performance.

For example, let’s consider the design of a rotating shaft for a generator. The generator produces electrical power by converting mechanical energy into electrical energy. The shaft connects the generator to the prime mover, which is typically an engine or a turbine that provides the mechanical power to rotate the shaft.

To design the shaft, the moment of inertia must be calculated. The moment of inertia depends on the mass distribution of the shaft and its geometry, such as its diameter and length. A common method to calculate the moment of inertia of a solid cylinder, which is a common shape for a shaft, is to use the formula:

I = (1/2) * m * r^2

where I is the moment of inertia, m is the mass of the cylinder, and r is the radius of the cylinder.

Once the moment of inertia is calculated, it can be used to determine the required strength and stiffness of the shaft to resist bending and torsion. The shaft must be strong enough to handle the loads imposed by the prime mover and the generator, while also being flexible enough to avoid excessive vibrations and stresses.

The moment of inertia also affects the energy storage and transfer capacity of the shaft. The higher the moment of inertia, the more energy the shaft can store and the smoother its rotation will be. However, a higher moment of inertia also means a heavier and more expensive shaft.

In summary, the mechanics moment of inertia is a critical parameter in the design of rotating shafts for machines such as generators. It affects the strength, stiffness, energy storage, and overall performance of the shaft, and must be carefully calculated and optimized to ensure the optimal design.

White paper on Mechanics Moment of Inertia

Introduction:

The moment of inertia is a fundamental property of a physical object that measures its resistance to rotational motion. It is a crucial parameter in mechanics and engineering, as it affects the stability, response, and performance of mechanical systems. This white paper will provide an overview of mechanics moment of inertia, its significance in engineering, and its applications in various fields.

What is Mechanics Moment of Inertia?

Mechanics moment of inertia is a measure of an object’s resistance to rotational motion around a specific axis. It depends on the mass distribution of the object and its geometry, such as its shape, size, and orientation relative to the axis of rotation. The moment of inertia is defined as the sum of the products of the mass of each particle in the object and the square of its distance from the axis of rotation.

The moment of inertia can be calculated for different shapes and structures, including beams, cylinders, spheres, plates, and more complex structures. The moment of inertia is a physical property that affects the object’s response to external forces and torques and determines its angular acceleration and angular momentum.

Significance of Mechanics Moment of Inertia:

The moment of inertia is a critical parameter in engineering and mechanics, as it affects the performance and stability of mechanical systems. It has several applications, including:

1. Design of rotating machinery: The moment of inertia is an essential parameter in the design of rotating machinery, such as engines, turbines, and generators. It affects the energy storage and transfer capacity of the rotating components and determines their ability to resist bending and torsion.
2. Design of structural elements: The moment of inertia is also important in the design of structural elements, such as beams, columns, and frames. It affects their strength and stiffness and determines their ability to resist deformation and failure.
3. Analysis of mechanical systems: The moment of inertia is a crucial parameter in the analysis of mechanical systems, such as vehicles, aircraft, and robots. It affects their response to external forces and torques and determines their stability and control.

Applications of Mechanics Moment of Inertia:

The moment of inertia has numerous applications in various fields, including:

1. Aerospace engineering: The moment of inertia is critical in the design and analysis of aerospace structures, such as satellites, rockets, and aircraft. It affects their stability, maneuverability, and control.
2. Automotive engineering: The moment of inertia is important in the design and analysis of automotive components, such as engines, transmissions, and wheels. It affects their performance, efficiency, and safety.
3. Robotics: The moment of inertia is essential in the design and control of robotic systems, such as manipulators, mobile robots, and drones. It affects their stability, accuracy, and agility.

Conclusion:

In summary, the mechanics moment of inertia is a fundamental property of physical objects that measures their resistance to rotational motion. It is a critical parameter in engineering and mechanics, as it affects the performance and stability of mechanical systems. The moment of inertia has numerous applications in various fields, including aerospace engineering, automotive engineering, and robotics. Therefore, it is essential to understand and optimize the moment of inertia in the design and analysis of mechanical systems to ensure their optimal performance and safety.