Conservation of angular momentum is a fundamental principle in physics that states that the total angular momentum of a system is conserved in the absence of external torques. Angular momentum is a property of rotating objects and is defined as the product of the moment of inertia and the angular velocity.

In simpler terms, the principle of conservation of angular momentum states that if an object is spinning or rotating, its speed or rate of rotation will remain constant as long as no external forces are acting on it. This principle has many applications in physics, including in the study of celestial mechanics, where it is used to explain the behavior of planets, stars, and other celestial bodies.

An important consequence of the conservation of angular momentum is that when a spinning object contracts, its rate of rotation increases due to the conservation of angular momentum. This is known as the conservation of angular momentum in a spinning system, and it is responsible for the formation of many celestial objects, such as stars and planets.

Overall, the conservation of angular momentum is a fundamental principle in physics that has many important applications and implications for the behavior of rotating objects in the universe.

What is Required Conservation of angular momentum

The conservation of angular momentum requires that the total angular momentum of a system remains constant in the absence of external torques. This means that if a system is spinning or rotating, its angular momentum cannot be created or destroyed, but can only be transferred between different parts of the system.

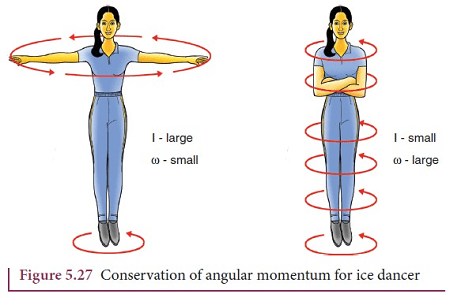
For example, if a spinning ice skater pulls in her arms, she reduces her moment of inertia, but her angular velocity increases so that her total angular momentum remains constant. This is because the conservation of angular momentum requires that any change in the moment of inertia must be compensated by an opposite change in the angular velocity.

Similarly, in the absence of external torques, the angular momentum of a planet in orbit around the sun is constant. This means that as the planet moves closer to the sun, its orbital speed increases to maintain a constant angular momentum.

The conservation of angular momentum is a fundamental principle in physics that has many important applications in mechanics, astrophysics, and other areas of science. It is a consequence of the rotational symmetry of physical laws, which states that the laws of physics are the same regardless of the orientation or direction of rotation of a system.

When is Required Conservation of angular momentum

The conservation of angular momentum is required whenever a system is undergoing rotational motion and there are no external torques acting on it. In such a case, the total angular momentum of the system remains constant, which means that any change in the angular velocity of one part of the system must be compensated by an opposite change in the moment of inertia of another part of the system.

The conservation of angular momentum applies to a wide range of systems, including:

1. Spinning objects: Any object that is rotating about its axis is subject to the conservation of angular momentum. This includes spinning tops, bicycle wheels, and planets.
2. Orbital motion: Any object that is in orbit around another object is subject to the conservation of angular momentum. This includes planets orbiting the sun, moons orbiting planets, and artificial satellites orbiting the Earth.
3. Collisions: When two objects collide, the total angular momentum of the system must be conserved. This means that the momenta and velocities of the objects must be adjusted in a way that conserves the total angular momentum of the system.
4. Fluid dynamics: The conservation of angular momentum also applies to fluids in motion, such as water flowing in a pipe or air moving in a tornado. In such systems, the angular momentum of the fluid remains constant, which can affect the behavior of the flow.

Overall, the conservation of angular momentum is a fundamental principle in physics that applies to many different types of systems and has many important applications in science and engineering.

Where is Required Conservation of angular momentum

The conservation of angular momentum is required in any physical system where there is rotational motion and no external torques are acting on the system. This can occur in a wide range of physical phenomena, including:

1. Astronomy: The conservation of angular momentum is important in astronomy because it explains many phenomena in the motion of celestial objects. For example, the rotation of planets and stars, the formation of planetary rings, and the motion of galaxies are all subject to the conservation of angular momentum.
2. Mechanics: The conservation of angular momentum is also important in mechanics because it governs the motion of rotating objects. Examples include the rotation of gears, the motion of a spinning top, and the behavior of a gyrocompass.
3. Fluid mechanics: The conservation of angular momentum is relevant in fluid mechanics because it governs the motion of fluids in rotation. Examples include the motion of water in a rotating container, the behavior of a whirlpool, and the flow of air in a tornado.
4. Particle physics: The conservation of angular momentum is also important in particle physics, where it plays a role in understanding the behavior of subatomic particles and the structure of atoms.

Overall, the conservation of angular momentum is a fundamental principle in physics that is relevant in many different areas of science and engineering. It is a consequence of the rotational symmetry of physical laws, which states that the laws of physics are the same regardless of the orientation or direction of rotation of a system.

How is Required Conservation of angular momentum

The conservation of angular momentum is a fundamental principle in physics that is based on the idea that the total angular momentum of a system is conserved in the absence of external torques. Mathematically, this principle is expressed as:

L = Iω

where L is the total angular momentum of the system, I is the moment of inertia of the system, and ω is the angular velocity of the system.

The principle of conservation of angular momentum states that if no external torques act on a system, then the total angular momentum of the system remains constant. This means that any changes in the angular velocity of one part of the system must be compensated by an opposite change in the moment of inertia of another part of the system.

For example, when a spinning figure skater pulls in their arms, they decrease their moment of inertia, but their angular velocity increases so that their total angular momentum remains constant. This is because the conservation of angular momentum requires that any change in the moment of inertia must be compensated by an opposite change in the angular velocity.

The conservation of angular momentum is a powerful principle that has many important applications in physics and engineering. It is used to explain the behavior of rotating systems, such as planets, stars, and other celestial bodies, and is also used in the design of machines, such as gyroscopes and flywheels.

Structures of Conservation of angular momentum

The conservation of angular momentum is a fundamental principle in physics that describes the behavior of rotating systems. There are several key structures that underpin this principle, including:

1. Moment of Inertia: The moment of inertia is a measure of an object’s resistance to rotational motion. It depends on the object’s mass distribution and the distance of the mass from the axis of rotation. The moment of inertia plays a crucial role in the conservation of angular momentum because any changes in the moment of inertia of a system must be compensated by an opposite change in the angular velocity of the system.
2. Angular Velocity: The angular velocity of a rotating system is the rate at which it rotates about its axis. It is measured in radians per second and is a key parameter in the conservation of angular momentum because it determines the amount of angular momentum that a system possesses.
3. Torque: Torque is a measure of the rotational force acting on an object. It is equal to the product of the force and the distance from the axis of rotation to the point where the force is applied. In the absence of external torques, the total angular momentum of a system remains constant, which means that any changes in the angular velocity of one part of the system must be compensated by an opposite change in the moment of inertia of another part of the system.
4. Rotational Symmetry: The conservation of angular momentum is based on the principle of rotational symmetry, which states that the laws of physics are the same regardless of the orientation or direction of rotation of a system. This principle is fundamental to the conservation of angular momentum because it implies that the total angular momentum of a system cannot be created or destroyed, but can only be transferred between different parts of the system.

Overall, the structures underlying the conservation of angular momentum are essential to understanding the behavior of rotating systems in physics and engineering. They provide a framework for analyzing the motion of spinning objects and have many important applications in a wide range of fields.

Case Study on Conservation of angular momentum

A classic example of the conservation of angular momentum can be seen in the motion of a figure skater. When a figure skater spins, their arms and legs are extended outward, which increases their moment of inertia and slows down their angular velocity. However, when they pull their arms and legs in towards their body, their moment of inertia decreases, which causes their angular velocity to increase. This phenomenon can be explained by the conservation of angular momentum.

Initially, when the skater is spinning with their arms and legs extended, they have a large moment of inertia and a slow angular velocity. According to the conservation of angular momentum, the total angular momentum of the system must remain constant. Therefore, when the skater pulls their arms and legs in towards their body, their moment of inertia decreases, which causes their angular velocity to increase. This increase in angular velocity compensates for the decrease in moment of inertia, and the total angular momentum of the system remains constant.

This example illustrates the importance of the conservation of angular momentum in understanding the behavior of rotating systems. The principle of conservation of angular momentum is a fundamental law of physics that underpins many phenomena in the motion of objects, including planets, stars, and other celestial bodies. It also has important applications in the design of machines, such as gyroscopes and flywheels, which rely on the conservation of angular momentum to maintain stable rotation.

In addition to the example of the figure skater, the conservation of angular momentum can be seen in a wide range of other physical phenomena, including the motion of planets and stars, the behavior of a spinning top, and the flow of fluids in rotation. Overall, the conservation of angular momentum is a powerful principle that plays a crucial role in our understanding of the motion of rotating systems.

White paper on Conservation of angular momentum

Introduction:

The conservation of angular momentum is a fundamental principle in physics that describes the behavior of rotating systems. It is based on the idea that the total angular momentum of a system is conserved in the absence of external torques. This principle has many important applications in physics and engineering, and is used to explain the behavior of rotating objects, including planets, stars, and other celestial bodies, as well as in the design of machines, such as gyroscopes and flywheels.

Moment of Inertia:

The moment of inertia is a measure of an object’s resistance to rotational motion. It depends on the object’s mass distribution and the distance of the mass from the axis of rotation. The moment of inertia plays a crucial role in the conservation of angular momentum because any changes in the moment of inertia of a system must be compensated by an opposite change in the angular velocity of the system.

Angular Velocity:

The angular velocity of a rotating system is the rate at which it rotates about its axis. It is measured in radians per second and is a key parameter in the conservation of angular momentum because it determines the amount of angular momentum that a system possesses. The higher the angular velocity, the greater the angular momentum of the system.

Torque:

Torque is a measure of the rotational force acting on an object. It is equal to the product of the force and the distance from the axis of rotation to the point where the force is applied. In the absence of external torques, the total angular momentum of a system remains constant, which means that any changes in the angular velocity of one part of the system must be compensated by an opposite change in the moment of inertia of another part of the system.

Rotational Symmetry:

The conservation of angular momentum is based on the principle of rotational symmetry, which states that the laws of physics are the same regardless of the orientation or direction of rotation of a system. This principle is fundamental to the conservation of angular momentum because it implies that the total angular momentum of a system cannot be created or destroyed, but can only be transferred between different parts of the system.

Applications:

The conservation of angular momentum has many important applications in physics and engineering. It is used to explain the behavior of rotating systems, such as planets, stars, and other celestial bodies, and is also used in the design of machines, such as gyroscopes and flywheels. It is also used in the study of fluid dynamics, where it is used to explain the behavior of rotating fluids, such as hurricanes and tornadoes.

Conclusion:

The conservation of angular momentum is a fundamental principle in physics that describes the behavior of rotating systems. It is based on the idea that the total angular momentum of a system is conserved in the absence of external torques. This principle has many important applications in physics and engineering, and is used to explain the behavior of rotating objects, as well as in the design of machines. Understanding the conservation of angular momentum is crucial to understanding the behavior of rotating systems, and it has many important applications in a wide range of fields.