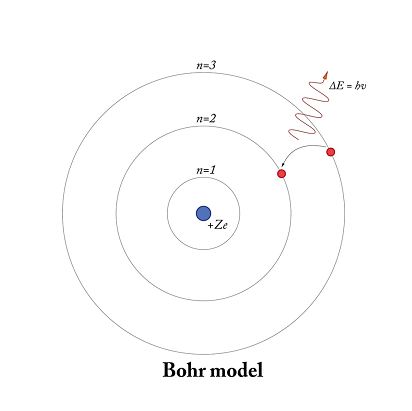
Bohr’s theory of hydrogen-like atoms is a model proposed by Niels Bohr in 1913 to explain the structure and behavior of atoms, particularly those with a single electron like hydrogen. The theory is based on the idea that electrons move in circular orbits around the nucleus of an atom, and that each orbit has a specific energy level.
Bohr’s theory of hydrogen-like atoms makes several key assumptions:
- Electrons in an atom can only occupy certain discrete energy levels, and they can transition between these levels by emitting or absorbing photons of energy.
- The energy of an electron in a particular orbit is proportional to the distance from the nucleus, and the electron can only occupy orbits with energies that correspond to specific values.
- The electron does not lose energy as it orbits the nucleus, unlike classical electromagnetic theory would predict. Instead, it remains in a stable orbit without radiating energy.
- The total angular momentum of the electron in a given orbit is quantized, meaning it can only take on certain discrete values.
Using these assumptions, Bohr was able to calculate the energy levels of hydrogen-like atoms and explain the observed spectral lines in their emission and absorption spectra. The theory was limited to hydrogen-like atoms, which have only one electron, but it provided a foundation for later quantum mechanical models that could describe more complex atoms and molecules.
What is Required Bohr’s theory of hydrogen-like atoms
Bohr’s theory of hydrogen-like atoms requires the following:
- Electrons move in circular orbits around the nucleus of an atom.
- The electron can only occupy certain discrete energy levels, and the energy of each level is proportional to the distance from the nucleus.
- Electrons can transition between energy levels by emitting or absorbing photons of energy, with the energy of the photon corresponding to the energy difference between the two levels.
- The electron does not lose energy as it orbits the nucleus, and it remains in a stable orbit without radiating energy.
- The total angular momentum of the electron in a given orbit is quantized, meaning it can only take on certain discrete values.
Bohr’s theory assumes that the electron is treated as a particle with a definite position and momentum, rather than a wave. It also assumes that the nucleus is stationary, which is not strictly true, but the approximation is valid for most purposes.
While Bohr’s theory of hydrogen-like atoms was an important step towards understanding atomic structure, it was limited to describing the behavior of atoms with one electron, and it was unable to explain some of the more complex behavior of atoms and molecules. However, it provided a foundation for later quantum mechanical models that could describe more complex systems.
When is Required Bohr’s theory of hydrogen-like atoms
Bohr’s theory of hydrogen-like atoms is required when we need to explain the behavior and structure of simple atoms with only one electron, such as hydrogen, helium, lithium, and beryllium. The theory provides a framework for understanding the discrete energy levels of these atoms and the transitions that occur between them, which are responsible for the spectral lines observed in their emission and absorption spectra.
Bohr’s theory is also useful for predicting the wavelengths of spectral lines in hydrogen-like atoms, which are important for a variety of applications in astronomy, chemistry, and physics. For example, the wavelengths of the hydrogen spectral lines can be used to study the composition and temperature of stars, and to identify the presence of hydrogen in interstellar gas clouds.
While Bohr’s theory is limited to simple atoms with one electron, it is still an important part of the foundation of modern quantum mechanics, which provides a more complete and accurate description of atomic and molecular behavior.
Where is Required Bohr’s theory of hydrogen-like atoms
Bohr’s theory of hydrogen-like atoms is required in various fields of science and technology where the behavior and properties of simple atoms with one electron need to be explained. Some of the areas where Bohr’s theory is used include:
- Atomic physics: Bohr’s theory provides a fundamental understanding of the energy levels and spectral lines of hydrogen-like atoms. It is used to study the behavior of atoms in various environments and to understand the interactions of atoms with electromagnetic radiation.
- Chemistry: The energy levels and spectral lines of hydrogen-like atoms are used in chemical analysis and the study of chemical reactions. The theory helps to explain the electronic structure of atoms and molecules, and how this structure affects their chemical properties.
- Astronomy: The spectral lines of hydrogen and other simple atoms provide important information about the composition and temperature of stars and other astronomical objects. Bohr’s theory is used to predict the wavelengths of these lines and to interpret the observations.
- Quantum mechanics: Bohr’s theory is an important part of the history of quantum mechanics and provides a foundation for understanding the more advanced theories that have been developed since then.
Overall, Bohr’s theory of hydrogen-like atoms is an essential part of our understanding of the behavior and properties of atoms and molecules, and it is used in a wide range of scientific and technological applications.
How is Required Bohr’s theory of hydrogen-like atoms
Bohr’s theory of hydrogen-like atoms is based on several key assumptions and principles, which help to explain the behavior and properties of simple atoms with one electron. The theory can be summarized as follows:
- Electrons move in circular orbits around the nucleus of an atom, and each orbit has a specific energy level.
- The electron can only occupy certain discrete energy levels, and the energy of each level is proportional to the distance from the nucleus.
- Electrons can transition between energy levels by emitting or absorbing photons of energy, with the energy of the photon corresponding to the energy difference between the two levels.
- The electron does not lose energy as it orbits the nucleus, and it remains in a stable orbit without radiating energy.
- The total angular momentum of the electron in a given orbit is quantized, meaning it can only take on certain discrete values.
Bohr’s theory also provides a mathematical framework for calculating the energy levels and spectral lines of hydrogen-like atoms. The energy of an electron in a particular orbit is given by the formula E = (-13.6 eV) / n^2, where n is the principal quantum number that corresponds to the energy level. The frequency of a photon emitted or absorbed during a transition between energy levels is given by the formula E = hf, where h is Planck’s constant and f is the frequency of the photon.
While Bohr’s theory is limited to simple atoms with one electron, it is still an important part of our understanding of atomic and molecular behavior, and it provides a foundation for more advanced quantum mechanical theories.
Nomenclature of Bohr’s theory of hydrogen-like atoms
Bohr’s theory of hydrogen-like atoms is named after its creator, Niels Bohr, a Danish physicist who proposed the theory in 1913. The theory is also sometimes referred to as the Bohr model or the Bohr-Sommerfeld model.
The theory is called the hydrogen-like atom because it was originally developed to explain the behavior of the hydrogen atom, which has one electron. However, the theory can also be applied to other atoms and ions that have a single electron in their outermost shell, such as helium, lithium, and beryllium.
In terms of nomenclature, the theory is based on the principles of quantum mechanics, which is a branch of physics that deals with the behavior of matter and energy at the atomic and subatomic level. The theory is therefore sometimes referred to as quantum mechanics in its simplest form.
The theory also introduced the concept of quantization, which refers to the discrete energy levels that electrons can occupy in an atom. This concept of quantization has been extended and refined in modern quantum mechanics, where it plays a central role in the description of the behavior of atoms and molecules.
Overall, Bohr’s theory of hydrogen-like atoms has had a profound impact on our understanding of atomic and molecular behavior, and it remains an important part of the foundation of modern physics.
Case Study on Bohr’s theory of hydrogen-like atoms
One notable application of Bohr’s theory of hydrogen-like atoms is in the field of astronomy, where it is used to study the spectra of stars and other astronomical objects. By analyzing the spectral lines of light emitted or absorbed by these objects, astronomers can determine their composition, temperature, and other properties.
One example of this is the study of the spectra of hydrogen in stars. Hydrogen is the most abundant element in the universe, and its spectral lines are among the most prominent features in the spectra of stars. By measuring the wavelengths of these lines, astronomers can determine the temperature and composition of the star’s outer layers, which are the regions where the hydrogen emission and absorption occur.
Bohr’s theory of hydrogen-like atoms provides a framework for understanding the energy levels and transitions that give rise to these spectral lines. The theory predicts that the hydrogen atom has discrete energy levels that correspond to the different orbits of the electron around the nucleus. When an electron transitions from a higher energy level to a lower one, it emits a photon of light with a specific wavelength that corresponds to the energy difference between the two levels.
Astronomers use this principle to identify the different spectral lines in the light emitted by stars, which can provide information about the temperature, composition, and other properties of the star. For example, the intensity and shape of the hydrogen spectral lines can be used to determine the temperature and density of the outer layers of the star, as well as its velocity relative to Earth.
In addition to hydrogen, other simple atoms with one electron, such as helium and lithium, also have distinctive spectral lines that can be studied using Bohr’s theory. By analyzing the spectral lines of these elements, astronomers can gain insights into the chemical composition and physical properties of stars, galaxies, and other astronomical objects.
Overall, Bohr’s theory of hydrogen-like atoms has had a significant impact on the study of astronomy and has helped astronomers to understand the composition and properties of the universe.
White paper on Bohr’s theory of hydrogen-like atoms
Introduction:
Bohr’s theory of hydrogen-like atoms, also known as the Bohr model or the Bohr-Sommerfeld model, is a significant contribution to the understanding of the behavior of simple atoms with one electron. The theory was proposed by Danish physicist Niels Bohr in 1913, and it is based on the principles of quantum mechanics. This white paper provides an overview of Bohr’s theory of hydrogen-like atoms, its key assumptions and principles, and its application in various fields.
Key Assumptions and Principles:
Bohr’s theory of hydrogen-like atoms is based on several key assumptions and principles. One of the most important assumptions is that electrons move in circular orbits around the nucleus of an atom, and each orbit has a specific energy level. The electron can only occupy certain discrete energy levels, and the energy of each level is proportional to the distance from the nucleus. Electrons can transition between energy levels by emitting or absorbing photons of energy, with the energy of the photon corresponding to the energy difference between the two levels.
Another key principle of Bohr’s theory is that the electron does not lose energy as it orbits the nucleus, and it remains in a stable orbit without radiating energy. This is known as the stability postulate, and it was a departure from classical physics, which predicted that a charged particle moving in a circular orbit would continuously emit energy in the form of electromagnetic radiation.
Bohr’s theory also introduced the concept of quantization, which refers to the discrete energy levels that electrons can occupy in an atom. The total angular momentum of the electron in a given orbit is quantized, meaning it can only take on certain discrete values.
Mathematical Framework:
Bohr’s theory provides a mathematical framework for calculating the energy levels and spectral lines of hydrogen-like atoms. The energy of an electron in a particular orbit is given by the formula E = (-13.6 eV) / n^2, where n is the principal quantum number that corresponds to the energy level. The frequency of a photon emitted or absorbed during a transition between energy levels is given by the formula E = hf, where h is Planck’s constant and f is the frequency of the photon.
Application in Various Fields:
Bohr’s theory of hydrogen-like atoms has had significant applications in various fields. In the field of chemistry, the theory has been used to explain the behavior of atoms and molecules and to predict the properties of chemical compounds. The theory has also been used in the study of atomic and molecular physics, where it has provided insights into the behavior of atoms and molecules under various conditions.
In addition, Bohr’s theory has had important applications in the field of astronomy, where it is used to study the spectra of stars and other astronomical objects. By analyzing the spectral lines of light emitted or absorbed by these objects, astronomers can determine their composition, temperature, and other properties. Bohr’s theory provides a framework for understanding the energy levels and transitions that give rise to these spectral lines, which can be used to study the properties of stars, galaxies, and other astronomical objects.
Conclusion:
Bohr’s theory of hydrogen-like atoms has had a profound impact on our understanding of atomic and molecular behavior, and it remains an important part of the foundation of modern physics. The theory has been applied in various fields, including chemistry, atomic and molecular physics, and astronomy, and it continues to provide insights into the behavior of matter and energy at the atomic and subatomic level.