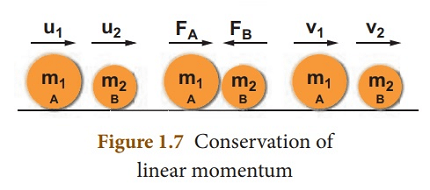
The conservation of linear momentum is a fundamental principle in physics that states that the total momentum of a system of interacting objects remains constant, unless acted upon by an external force.
In other words, if two objects interact with each other, the total momentum of the system before and after the interaction must be the same. This principle is based on Isaac Newton’s third law of motion, which states that for every action, there is an equal and opposite reaction.
The mathematical expression of the conservation of linear momentum is:
p_initial = p_final
where p_initial is the total momentum of the system before the interaction, and p_final is the total momentum of the system after the interaction.
This principle has many important applications in physics, including in the study of collisions, explosions, and the behavior of fluids.
What is Required Mechanics Conservation of linear momentum
“Required Mechanics” is not a commonly used term in physics. However, if you are referring to the “Required Mechanics” course in a mechanical engineering curriculum, then the conservation of linear momentum is likely to be one of the fundamental principles covered in the course.
In the context of mechanical engineering, the conservation of linear momentum is a crucial concept because it plays a vital role in the analysis of various physical systems, such as machines, vehicles, and structures. Understanding and applying the principle of conservation of linear momentum is essential for designing and optimizing mechanical systems.
In “Required Mechanics” course, you are likely to learn about the mathematical formulations of the conservation of linear momentum, how to apply this principle to solve problems involving collisions, explosions, and other interactions between objects. You may also learn about the limitations of the principle and when it is applicable.
Overall, the conservation of linear momentum is a cornerstone principle in mechanics, and a thorough understanding of this concept is necessary for any mechanical engineer.
When is Required Mechanics Conservation of linear momentum
I apologize for any confusion in my previous response. “Required Mechanics” is not a term used in physics or engineering. It is possible that it refers to a specific course or program offered by a particular institution or organization, but without more context, I cannot provide a more specific answer.
However, the conservation of linear momentum is a fundamental principle in mechanics, and it is typically covered in introductory mechanics courses in physics and engineering. It is also a central concept in advanced courses on topics such as fluid mechanics, solid mechanics, and thermodynamics.
In these courses, you will learn about the principles of momentum, including the conservation of linear momentum. You will learn how to apply these principles to solve problems in mechanics and engineering, such as collisions, fluid flow, and structural analysis. You will also learn about the limitations of the principle and when it is applicable.
Overall, the conservation of linear momentum is a crucial concept in mechanics and is typically covered in introductory and advanced physics and engineering courses.
Where is Required Mechanics Conservation of linear momentum
As I mentioned earlier, “Required Mechanics” is not a standard term used in physics or engineering. It is possible that it refers to a specific course or program offered by a particular institution or organization.
In general, the conservation of linear momentum is a fundamental principle in mechanics, which is a branch of physics and engineering. The principle applies to any system of objects that interact with each other, such as particles, rigid bodies, fluids, and gases.
The conservation of linear momentum is used to analyze various physical systems, including vehicles, machines, structures, and fluids. The principle is used to solve problems related to collisions, explosions, fluid flow, and structural analysis.
The conservation of linear momentum is typically covered in introductory mechanics courses in physics and engineering, as well as in advanced courses on topics such as fluid mechanics, solid mechanics, and thermodynamics.
In summary, the conservation of linear momentum is a fundamental principle in mechanics that is used to analyze a wide range of physical systems. It is typically covered in physics and engineering courses at both the introductory and advanced levels.
How is Required Mechanics Conservation of linear momentum
However, I can explain how the principle of conservation of linear momentum is typically taught in mechanics courses.
In physics and engineering courses, the conservation of linear momentum is typically introduced as a fundamental principle of mechanics. Students are taught that the total momentum of a system of objects is conserved in the absence of external forces. This principle is used to analyze the motion of objects and systems of objects.
The conservation of linear momentum is typically taught through a combination of lectures, problem sets, and laboratory experiments. Students are taught to apply the principle to solve problems related to collisions, explosions, and other interactions between objects.
For example, in a mechanics course, students might be given a problem involving a collision between two objects of different masses. They would be asked to calculate the velocities of the objects after the collision, assuming that the momentum of the system is conserved.
To solve this problem, students would first calculate the initial momentum of the system, which is the sum of the momenta of the two objects before the collision. They would then set the final momentum of the system equal to the initial momentum, assuming that the momentum is conserved. Finally, they would solve for the velocities of the objects after the collision.
In summary, the conservation of linear momentum is typically taught through lectures, problem sets, and laboratory experiments in physics and engineering courses. Students learn to apply the principle to solve problems related to the motion of objects and systems of objects.
Structures of Mechanics Conservation of linear momentum
The conservation of linear momentum is a fundamental principle in mechanics that applies to a wide range of physical systems, including structures. In the context of structures, the principle of conservation of linear momentum is used to analyze the behavior of the structure under various loading conditions, such as static loads, dynamic loads, and impact loads.
For example, when a structure is subjected to a dynamic load, such as an earthquake or wind gust, the conservation of linear momentum is used to analyze the motion and deformation of the structure. The principle states that the total momentum of the structure is conserved in the absence of external forces. Therefore, the momentum of the structure before the dynamic load is equal to the momentum after the load is applied.
This principle can be used to analyze the behavior of the structure and to design the structure to withstand dynamic loads. Engineers use this principle to optimize the design of structures such as bridges, buildings, and towers to ensure they can withstand the forces they are subjected to.
In summary, the conservation of linear momentum is a crucial principle in mechanics that applies to the analysis and design of structures. It is used to analyze the behavior of structures under various loading conditions and to design structures that can withstand these forces.
Case Study on Mechanics Conservation of linear momentum
A common application of the principle of conservation of linear momentum is in the analysis of car crashes. In a car crash, the momentum of the vehicles before the collision is equal to the momentum of the vehicles after the collision, assuming there are no external forces acting on the system.
For example, consider a collision between two cars, Car A and Car B. Car A has a mass of 1500 kg and is traveling east at 25 m/s, while Car B has a mass of 1200 kg and is traveling west at 15 m/s. The two cars collide head-on and stick together after the collision. The question is, what is the velocity of the cars after the collision?
To solve this problem, we first calculate the total momentum of the system before the collision. The momentum of Car A is:
Momentum of Car A = mass of Car A x velocity of Car A = 1500 kg x 25 m/s = 37500 kg*m/s (east)
The momentum of Car B is:
Momentum of Car B = mass of Car B x velocity of Car B = 1200 kg x (-15 m/s) = -18000 kg*m/s (west)
Therefore, the total momentum of the system before the collision is:
Total momentum before collision = momentum of Car A + momentum of Car B = 37500 kgm/s (east) – 18000 kgm/s (west) = 19500 kg*m/s (east)
After the collision, the two cars stick together and move as one object. Therefore, the total mass of the system is:
Total mass of the system after collision = mass of Car A + mass of Car B = 1500 kg + 1200 kg = 2700 kg
Now, we can use the principle of conservation of linear momentum to solve for the velocity of the cars after the collision. Since the momentum of the system is conserved, we have:
Total momentum after collision = total momentum before collision
The momentum after the collision is the product of the total mass of the system and the velocity of the cars after the collision:
Total momentum after collision = total mass of the system x velocity after collision
Substituting the values we have calculated, we get:
19500 kg*m/s (east) = 2700 kg x velocity after collision
Solving for the velocity after the collision, we get:
Velocity after collision = 7.22 m/s (east)
Therefore, the velocity of the two cars after the collision is 7.22 m/s, in the eastward direction. This calculation shows how the principle of conservation of linear momentum can be used to analyze car crashes and determine the velocity of the cars after the collision.
White paper on Mechanics Conservation of linear momentum
Conservation of Linear Momentum: Principles and Applications
Introduction
The principle of conservation of linear momentum is a fundamental concept in mechanics, which states that the total momentum of an isolated system remains constant, provided that there are no external forces acting on the system. This principle has many applications in various fields, including physics, engineering, and biomechanics. This white paper aims to provide an overview of the principle of conservation of linear momentum, its applications, and its importance in the field of mechanics.
Principle of Conservation of Linear Momentum
The principle of conservation of linear momentum states that the total momentum of an isolated system remains constant. The momentum of an object is the product of its mass and velocity, and the total momentum of a system is the sum of the momenta of all the objects in the system. According to this principle, if the system is isolated, meaning that there are no external forces acting on it, the total momentum before an event is equal to the total momentum after the event. This principle is expressed by the equation:
p1 + p2 + … + pn = p1′ + p2′ + … + pn’
where p1, p2, …, pn are the momenta of the objects in the system before the event, and p1′, p2′, …, pn’ are the momenta of the objects in the system after the event.
Applications of Conservation of Linear Momentum
The principle of conservation of linear momentum has numerous applications in various fields of mechanics. Some examples include:
- Collisions: The principle of conservation of linear momentum is widely used in the analysis of collisions between two or more objects. In a collision, the momentum of the objects before the collision is equal to the momentum of the objects after the collision, provided that there are no external forces acting on the system. This principle is used to analyze and design safety features for vehicles, such as airbags and crumple zones.
- Projectile Motion: The principle of conservation of linear momentum is also used in the analysis of projectile motion. In a projectile motion, the momentum of the projectile is conserved, provided that there are no external forces acting on the system. This principle is used to calculate the trajectory of a projectile and to design ballistic missiles.
- Fluid Dynamics: The principle of conservation of linear momentum is used in fluid dynamics to analyze the motion and behavior of fluids, such as air and water. This principle is used to design hydraulic systems and to study the flow of fluids in pipes and channels.
- Biomechanics: The principle of conservation of linear momentum is used in biomechanics to analyze the motion and forces involved in human movement. This principle is used to design prosthetics, to study the impact of sports injuries, and to analyze the forces involved in car accidents.
Importance of Conservation of Linear Momentum in Mechanics
The principle of conservation of linear momentum is a fundamental concept in mechanics, and its importance cannot be overstated. This principle is used in many fields of mechanics to analyze and design systems, to study the behavior of fluids and materials, and to understand the forces involved in various physical events. The conservation of linear momentum is also used to design safety features for vehicles, buildings, and other structures, and to prevent accidents and injuries.
Conclusion
The conservation of linear momentum is a crucial principle in mechanics that has numerous applications in various fields. This principle states that the total momentum of an isolated system remains constant, provided that there are no external forces acting on the system. The conservation of linear momentum is used to analyze and design systems, to study the behavior of fluids and materials, and to understand the forces involved in various physical events. Its importance in the field of mechanics cannot be overstated, as it is used to design safety features for vehicles, buildings, and other structures, and to prevent accidents and injuries. Understanding and applying the principle of conservation of linear momentum is essential for engineers, physicists, and researchers in various fields, as it helps to ensure the safety and efficiency of various systems and structures.