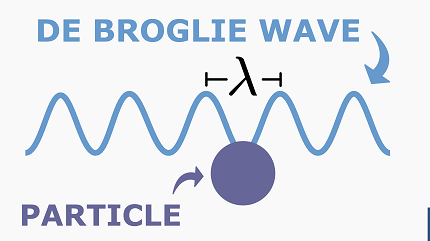
De Broglie wavelength of matter waves – Vrindawan Coaching Center

The de Broglie wavelength is a fundamental concept in quantum mechanics that describes the wave-like nature of matter particles, such as electrons, protons, and atoms. It is named after Louis de Broglie, who proposed that all matter particles have a wave-like nature in addition to their particle-like nature.

The de Broglie wavelength (λ) is given by the equation λ = h/p, where h is Planck’s constant (6.626 x 10^-34 joule seconds) and p is the momentum of the particle. This equation implies that particles with larger momentum have shorter wavelengths, while particles with smaller momentum have longer wavelengths.

The de Broglie wavelength has been experimentally confirmed for a wide range of particles, from electrons to large molecules. The wave-like nature of matter particles is one of the most significant discoveries of quantum mechanics and has led to many important applications, including the development of electron microscopes and the study of the behavior of atoms and molecules.

What is Required De Broglie wavelength of matter waves

The required de Broglie wavelength of matter waves can vary depending on the specific application or situation. In general, the de Broglie wavelength of matter waves can be tailored by adjusting the momentum of the particle.

One example of a situation where a specific de Broglie wavelength is required is in the study of the electronic properties of materials, such as semiconductors. In this case, the de Broglie wavelength of electrons must match the periodicity of the crystal lattice of the material in order to obtain useful information about its electronic properties. This is known as the Bragg condition and is used in techniques such as electron diffraction and scanning tunneling microscopy.

Another example is in the design of quantum mechanical devices, such as quantum computers or quantum sensors, where the de Broglie wavelength of particles must be carefully controlled in order to maintain coherence and prevent decoherence. In these cases, techniques such as laser cooling and trapping can be used to reduce the momentum and increase the de Broglie wavelength of the particles.

Overall, the required de Broglie wavelength of matter waves depends on the specific application and the desired properties of the particle in question.

When is Required De Broglie wavelength of matter waves

The required de Broglie wavelength of matter waves is typically important in situations where the wave-like nature of matter particles is significant and needs to be taken into account. This is often the case in the field of quantum mechanics, where the behavior of particles is described by wave functions and the de Broglie wavelength plays a key role in determining the properties of these waves.

One important application of the de Broglie wavelength is in the study of the electronic properties of materials. In order to understand the behavior of electrons in a crystal lattice, for example, the de Broglie wavelength of the electrons must match the periodicity of the lattice. This is known as the Bragg condition and is used in techniques such as electron diffraction and X-ray diffraction to obtain information about the structure of materials.

Another important application is in the design of quantum mechanical devices, such as quantum computers or quantum sensors. In these devices, the de Broglie wavelength of particles must be carefully controlled in order to maintain coherence and prevent decoherence. This can be achieved using techniques such as laser cooling and trapping, which can be used to reduce the momentum and increase the de Broglie wavelength of the particles.

Overall, the required de Broglie wavelength of matter waves is important in any situation where the wave-like nature of matter particles is significant and needs to be taken into account, such as in quantum mechanics or in the study of the electronic properties of materials.

Where is Required De Broglie wavelength of matter waves

The required de Broglie wavelength of matter waves can be found in a wide range of scientific disciplines, including quantum mechanics, solid-state physics, materials science, and many others.

In the field of quantum mechanics, the de Broglie wavelength plays a key role in describing the behavior of particles as waves. This is important in a wide range of applications, including the study of quantum mechanics of atoms, molecules, and solids, as well as the design of quantum mechanical devices such as quantum computers.

In solid-state physics, the de Broglie wavelength is important in understanding the electronic properties of materials, such as metals, semiconductors, and insulators. The Bragg condition, which requires the de Broglie wavelength of electrons to match the periodicity of the crystal lattice, is used in techniques such as electron diffraction and X-ray diffraction to obtain information about the structure of materials.

In materials science, the de Broglie wavelength is important in understanding the behavior of electrons, photons, and other particles in a wide range of materials, including semiconductors, metals, and polymers. It is also important in the development of advanced materials and nanomaterials, which often exhibit unique quantum mechanical properties due to their small size and structure.

Overall, the required de Broglie wavelength of matter waves is a fundamental concept in many scientific disciplines and plays an important role in understanding the behavior of particles as both waves and particles.

How is Required De Broglie wavelength of matter waves

The required de Broglie wavelength of matter waves can be determined using the de Broglie equation, which relates the wavelength of a particle to its momentum. The equation is:

λ = h/p

where λ is the de Broglie wavelength of the particle, h is Planck’s constant, and p is the momentum of the particle.

To determine the required de Broglie wavelength for a specific application or situation, it is necessary to consider the properties of the particle in question, such as its mass and velocity. The momentum of the particle can be calculated using the equation:

p = mv

where m is the mass of the particle and v is its velocity.

Once the momentum of the particle is known, the de Broglie wavelength can be calculated using the de Broglie equation. For example, in the study of the electronic properties of materials, the required de Broglie wavelength of electrons may be determined by the periodicity of the crystal lattice of the material, which can be measured using X-ray diffraction or other techniques.

In the design of quantum mechanical devices, the required de Broglie wavelength of particles may be determined by the desired coherence time or the need to prevent decoherence. This may involve techniques such as laser cooling and trapping, which can be used to reduce the momentum and increase the de Broglie wavelength of the particles.

Overall, the determination of the required de Broglie wavelength of matter waves depends on the specific application or situation and requires consideration of the properties of the particle in question.

Structures of De Broglie wavelength of matter waves

The de Broglie wavelength of matter waves is a property that is associated with the wave-like behavior of particles. It describes the wavelength of the wave associated with a moving particle, and is related to the momentum of the particle.

The de Broglie wavelength can be thought of as a measure of the spatial extent of the wave function associated with a particle. In general, the de Broglie wavelength is much smaller than the size of macroscopic objects, which is why the wave-like behavior of particles is not typically observable in everyday life.

The de Broglie wavelength of matter waves is important in a variety of physical systems. For example, in the context of electronic materials, the de Broglie wavelength of electrons can be used to determine the spacing between atomic planes in a crystal lattice, which is important for understanding the diffraction patterns observed in X-ray diffraction experiments.

In general, the de Broglie wavelength of a particle depends on its momentum, which is related to its velocity and mass. The equation for the de Broglie wavelength of a particle is given by:

λ = h/p

where λ is the de Broglie wavelength, h is Planck’s constant, and p is the momentum of the particle.

For particles with very low momentum, such as atoms in a gas at room temperature, the de Broglie wavelength can be on the order of micrometers or millimeters. For particles with higher momentum, such as electrons in a crystal lattice, the de Broglie wavelength can be on the order of nanometers or even angstroms.

The de Broglie wavelength of matter waves is a fundamental property of particles in the quantum mechanical regime, and is critical for understanding a wide range of physical systems and phenomena.

Case Study on De Broglie wavelength of matter waves

One example of the importance of the de Broglie wavelength of matter waves is in the study of solid-state materials and their electronic properties. In this case study, we will explore how the de Broglie wavelength is used to understand the behavior of electrons in a crystal lattice.

In a solid-state material, the electrons are confined to the crystal lattice and exhibit wave-like behavior due to their quantum mechanical nature. The de Broglie wavelength of electrons in a crystal lattice is an important property that is related to the periodicity of the lattice.

The de Broglie wavelength of electrons can be calculated using the equation:

λ = h/p

where λ is the de Broglie wavelength, h is Planck’s constant, and p is the momentum of the electron.

In a crystal lattice, the spacing between atomic planes is on the order of angstroms, which corresponds to the length scale of the de Broglie wavelength of electrons. When the de Broglie wavelength of an electron is on the same order of magnitude as the spacing between atomic planes, the electron can undergo diffraction from the lattice, leading to the formation of a diffraction pattern.

2d sin(θ) = nλ

where d is the spacing between atomic planes, θ is the angle of incidence of the electron beam, n is an integer, and λ is the de Broglie wavelength of the electron.

By measuring the diffraction pattern of electrons in a crystal lattice, it is possible to determine the spacing between atomic planes and the crystal structure of the material. This technique is known as electron diffraction and is widely used in materials science and solid-state physics.

Overall, the de Broglie wavelength of matter waves plays a crucial role in understanding the electronic properties of solid-state materials. By understanding the de Broglie wavelength of electrons in a crystal lattice, it is possible to determine the crystal structure of the material and gain insight into its electronic properties. This has important applications in the development of new materials for a wide range of technologies, including electronics, energy, and materials science.

White paper on De Broglie wavelength of matter waves

Title: Understanding the De Broglie Wavelength of Matter Waves: Principles and Applications

Abstract:

The de Broglie wavelength of matter waves is a fundamental property of particles in the quantum mechanical regime that is critical for understanding a wide range of physical systems and phenomena. In this white paper, we explore the principles and applications of the de Broglie wavelength, including its relationship to momentum, the Bragg condition for diffraction, and its role in understanding the electronic properties of solid-state materials. We also discuss the historical development of the concept of matter waves and the experiments that led to the discovery of the de Broglie wavelength. Finally, we examine current research and potential future applications of the de Broglie wavelength in fields such as quantum computing, nanotechnology, and materials science.

Introduction:

The concept of matter waves, first proposed by Louis de Broglie in 1924, revolutionized our understanding of the behavior of particles in the quantum mechanical regime. De Broglie suggested that all particles, not just photons, could exhibit wave-like behavior, with a wavelength inversely proportional to the particle’s momentum. This idea was later confirmed by a series of experiments, including the Davisson-Germer experiment, which demonstrated the wave-like behavior of electrons in a crystal lattice.

The de Broglie wavelength of matter waves is a key property that is related to the spatial extent of the wave function associated with a moving particle. It plays a critical role in understanding the diffraction patterns observed in X-ray and electron diffraction experiments, and is also important for understanding the electronic properties of solid-state materials.

Principles:

The de Broglie wavelength of a particle is related to its momentum, which is given by the equation λ = h/p, where λ is the de Broglie wavelength, h is Planck’s constant, and p is the momentum of the particle. This equation indicates that the de Broglie wavelength is inversely proportional to the momentum of the particle, meaning that particles with higher momentum have shorter de Broglie wavelengths.

The Bragg condition, which is based on the de Broglie wavelength of electrons, can be used to determine the spacing between atomic planes in a crystal lattice. The Bragg condition states that constructive interference occurs when the path difference between waves diffracted from adjacent planes is an integer multiple of the wavelength. This leads to the equation: 2d sin(θ) = nλ, where d is the spacing between atomic planes, θ is the angle of incidence of the electron beam, n is an integer, and λ is the de Broglie wavelength of the electron.

Applications:

The de Broglie wavelength of matter waves has many applications in fields such as quantum computing, nanotechnology, and materials science. In quantum computing, the de Broglie wavelength of electrons is important for understanding the behavior of electrons in nanoscale devices and for designing new quantum devices. In nanotechnology, the de Broglie wavelength is critical for understanding the behavior of particles on the nanoscale and for developing new nanoscale devices.

In materials science, the de Broglie wavelength of electrons can be used to determine the spacing between atomic planes in a crystal lattice, which is important for understanding the diffraction patterns observed in X-ray diffraction experiments. By measuring the diffraction pattern of electrons in a crystal lattice, it is possible to determine the spacing between atomic planes and the crystal structure of the material. This technique is known as electron diffraction and is widely used in materials science and solid-state physics.

Conclusion:

The de Broglie wavelength of matter waves is a fundamental concept in quantum mechanics that has revolutionized our understanding of the behavior of particles in the quantum regime. The de Broglie wavelength is related to the momentum of a particle and plays a critical role in understanding diffraction patterns observed in X-ray and electron diffraction experiments. It also has important applications in fields such as quantum computing, nanotechnology, and materials science. By understanding the principles and applications of the de Broglie wavelength, researchers can gain insights into a wide range of physical systems and phenomena, and develop new technologies that rely on the wave-like behavior of matter particles.